2. Найти начальный опорный план:
а) методом северо-западного угла;
б) методом минимальной стоимости.
Решить задачу методом потенциалов.
а)
Таблица 16
| Площадка | №1 | №2 | №3 | Отгрузка |
| Завод 1 | 30 | 40 | 50 | а 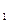 = 120 = 120
|
| Завод 2 | 20 | 30 | 40 | а 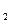 = 100 = 100
|
| Заказ | b 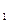 = 70 = 70
| b 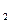 = 80 = 80
| b 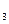 = 70 = 70
|
б)
Таблица 17
| Площадка | №1 | №2 | №3 | Отгрузка |
| Завод 1 | 40 | 60 | 80 | а 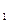 = 150 = 150
|
| Завод 2 | 90 | 30 | 50 | а 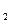 = 100 = 100
|
| Заказ | b 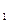 = 110 = 110
| b 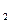 = 80 = 80
| b 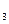 = 60 = 60
|
в)
Таблица 18
| Площадка | №1 | №2 | №3 | Отгрузка |
| Завод 1 | 70 | 40 | 60 | а 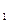 = 120 = 120
|
| Завод 2 | 30 | 80 | 50 | а 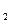 = 80 = 80
|
| Заказ | b 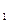 = 70 = 70
| b 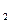 = 80 = 80
| b 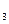 = 50 = 50
|
г)
Таблица 19
| Площадка | №1 | №2 | №3 | Отгрузка |
| Завод 1 | 90 | 40 | 70 | а 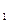 = 150 = 150
|
| Завод 2 | 60 | 80 | 50 | а 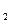 = 100 = 100
|
| Заказ | b 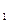 = 50 = 50
| b 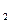 = 80 = 80
| b 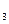 = 120 = 120
|
д)
Таблица 20
| Площадка | №1 | №2 | №3 | Отгрузка |
| Завод 1 | 60 | 30 | 80 | а 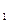 = 100 = 100
|
| Завод 2 | 20 | 70 | 40 | а 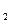 = 140 = 140
|
| Заказ | b 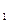 = 80 = 80
| b 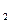 = 90 = 90
| b 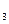 = 70 = 70
|
Задание №2. Другие модели транспортной задачи (найти оптимальные план перевозки груза).
Задача 1. Торговый дом "Дока-хлеб" закупил пшеницу в Гданьске, Оренбурге и Краснодаре. Ее необходимо доставить в четыре филиала фирмы в Москве, Петербурге, Твери и Туле. Тарифы на доставку одной тонны пшеницы, объемы закупок и требуемое количество даны в таблицах по вариантам. Стоимость хранения в Гданьске, Оренбурге и Краснодаре 1 т зерна составляет соответственно с1, с2 и с3. Найдите оптимальный план поставок пшеницы, выполняемых торговым домом «Дока -хлеб».
а)
Таблица 21
| Москва | Санкт-Петербург | Тверь | Тула | Объем закупки | ||||||||||||||
| Гданьск | 300 | 100 | 150 | 250 | 450 | ||||||||||||||
| Краснодар | 300 | 400 | 350 | 200 | 550 | ||||||||||||||
| Оренбург | 250 | 300 | 200 | 300 | 600 | ||||||||||||||
| Заказ | 600 | 500 | 200 | 100 | |||||||||||||||
с1=250, с2=200, с3=150
б)
Таблица 22
| Москва | Санкт-Петербург | Тверь | Тула | Объем закупки | ||||||||||||||
| Гданьск | 200 | 300 | 250 | 150 | 550 | ||||||||||||||
| Краснодар | 300 | 400 | 300 | 250 | 650 | ||||||||||||||
| Оренбург | 150 | 250 | 200 | 200 | 800 | ||||||||||||||
| Заказ | 450 | 700 | 300 | 300 | |||||||||||||||
с1=200, с2=100, с3=150
в)
Таблица 23
| Москва | Санкт-Петербург | Тверь | Тула | Объем закупки | ||||||||||||||
| Гданьск | 200 | 300 | 250 | 150 | 650 | ||||||||||||||
| Краснодар | 250 | 400 | 300 | 250 | 750 | ||||||||||||||
| Оренбург | 150 | 250 | 200 | 200 | 600 | ||||||||||||||
| Заказ | 500 | 750 | 400 | 300 | |||||||||||||||
с1=200, с2=100, с3=150.
Задача 2. Четыре магазина «Лига-плюс», «Умка», «Гурман» и «Улей» торгуют молочной продукцией , которую поставляют 3 молокозавода. Один из этих заводов - №1 имеет соглашение с фирменным магазином "Гурман" о фиксированной поставке ему своей продукции. Тарифы на доставку молочной продукции и объем фиксированной поставки (в ящиках) даны в таблицах по вариантам. Найдите оптимальный план поставок молочной продукции.
а)
Таблица 24
| «Лига-плюс» | «Гурман» | «Умка» | «Улей» | Объем закупки | ||||||||||||||
| №1 | 5 |
200 | 6 | 10 | 700 | ||||||||||||||
| №2 | 9 | 6 | 7 | 5 | 800 | ||||||||||||||
| №3 | 6 | 7 | 5 | 8 | 500 | ||||||||||||||
| Заказ | 800 | 400 | 600 | 200 | |||||||||||||||
б)
Таблица 25
| «Лига-плюс» | «Гурман» | «Умка» | «Улей» | Объем закупки | ||||||||||||||
| №1 | 5 |
300 | 10 | 7 | 400 | ||||||||||||||
| №2 | 6 | 8 | 5 | 8 | 600 | ||||||||||||||
| №3 | 7 | 9 | 6 | 4 | 900 | ||||||||||||||
| Заказ | 500 | 700 | 200 | 500 | |||||||||||||||
III. К разделу «Комбинаторика»:
Задание №3.
Таблица 26
| Вариант № | Задания |
| 1 | 2 | ||
| I | а) Комиссия состоит из председателя, его заместителя и еще пяти человек. Сколькими способами члены комиссии могут распределить между собой обязанности? б) Чемпионат, в котором участвуют 16 команд, проводится в два круга (т. е. каждая команда дважды встречается с любой другой). Определить, какое количество встреч следует провести. в) Две ладьи различного цвета расположены на шахматной доске так, что каждая может взять другую. Сколько существует таких расположений? | ||
| II | а) Сколькими способами можно выбрать трех дежурных из группы в 20 человек? б) Замок открывается только в том случае, если набран определенный трсхзначный номер. Попытка состоит в том, что набирают наугад три цифры из заданных пяти цифр. Угадать номер удалось только на последней из всех возможных попыток. Сколько попыток предшествовало удачной? в) Порядок выступления восьми участников конкурса определяется жребием. Сколько различных исходов жеребьевки при этом возможно? | ||
| III | а) Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти звуков? б) Из группы в 15 человек выбирают четырех участников эстафеты 800 + 400 + 200 + 100 Сколькими способами можно расставить спортсменов по этапам эстафеты? в) На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом первый и второй тома не стояли рядом? | ||
| IV | а) В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета?
в) Поезд метро делает 16 остановок, на которых выходят все пассажиры. Сколькими способами могут распределиться между этими остановками 100 пассажиров, вошедших в поезд на конечной остановке? | ||
| V | а) Номера трамвайных маршрутов иногда обозначаются двумя цветными фонарями. Какое количество различных маршрутов можно обозначить, если использовать фонари восьми цветов? б) Сколькими способами можно расположить на шахматной доске две ладьи так, чтобы одна не могла взять другую? (Одна ладья может взять другую, если она находится с ней на одной горизонтали или на одной вертикали шахматной доски.) в) Сколько трехзначных чисел, делящихся на З, можно составить из цифр 0, 1, 2, 3, 4, 5, если каждое число не должно содержать одинаковых цифр? |
IV. К разделу «Теория вероятностей»:
Задание №4.
Таблица 27
| а) классическое и статистическое определение вероятности | |
| Вариант № | Задание |
| 1 | 2 | ||
| I | Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях четная, причем на грани одной из костей появится шестерка. | ||
| II | При перевозке ящика, в котором содержалась 21 стандартная и 10 нестандартных деталей, утеряна одна деталь, причем не известно, какая. Наудачу извлеченная (после перевозки ящика) деталь оказалась стандартной. Найти вероятность того, что была утеряна: а) стандартная деталь; б) нестандартная деталь. | ||
| III | Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того , что наудачу извлеченный кубик имеет: а) одну окрашенную грань; б) две окрашенные грани; в) три окрашенные грани. | ||
| IV | В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная. | ||
| V | В коробке пять одинаковых деталей, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия; в) хотя бы одно окрашенное изделие. | ||
| |||
| I | На стеллаже библиотеки в случайном порядке расставлены 15 учебников., причем 5 из них в переплете. Библиотекарь наудачу выбирает три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете. | ||
| II | В ящике 10 деталей, из которых 4 окрашены. Сборщик взял наудачу 3 детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена. | ||
| III | Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,95, а вероятность того, что при аварии сработает второй сигнализатор, равна 0,9. Найти вероятность того, что при аварии сработает только один сигнализатор | ||
| IV | Два стрелка стреляют по мишени. Вероятность попадания в мишень при первом выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при первом залпе в мишень попадет только один из стрелков. | ||
| V | Из партии товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий только два изделия высшего сорта. | ||
| в) вероятность появления хотя бы одного события | |||
| I | В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны p1=0.1, p2=0.15, p3=0.2, Найти вероятность того, что тока в цепи не будет. | ||
| II | Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятность отказа устройства, если достаточно, чтобы отказал хотя бы один элемент. | ||
| III | Для разрушения моста достаточно попадании одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны : 0,3, 0,4, 0,6, 07. | ||
| IV | Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875. Найти вероятность попадания при одном выстреле. | ||
| V | Вероятность успешного выполнения упражнения для каждого из двух спортсменов равна 0,5. Спортсмены выполняют упражнение по очереди, причем каждый делает по две попытки. Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами. | ||
| г) формула полной вероятности | |||
| I | В урну, содержащую два шара, спущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету). | ||
| II | В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того. что стрелок поразит мишень при выстреле из вин
| ||
| III | В первой урне содержится 10 шаров, из них 8 белых, во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров был наудачу взят один шар. Найти вероятность того, что взят белый шар. | ||
| IV | В каждой из трех ури содержится б черных с 4 белых шара. 1Iз первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен одни шар н переложен в третью урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым. | ||
| V | В ящике содержится 12 деталей, изготовленных на заводе № 1, 20 деталей, изготовленных на заводе№2 и 18 деталей, изготовленных на заводе №3. Вероятность того. что деталь изготовленная на заводе №1, отличного качества, равна 0,9; для деталей, изготовленных на заводах №2 и №3, эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества. | ||
| д) основные формулы теории вероятностей | |||
| I | В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок сразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него? | ||
| II | В специализированную больницу поступают в среднем 50% больных с заболеванием А, 30%—с заболеванием Б, 20%—с заболеванием С. Вероятность полного излечения болезни А равна 0,7; для болезней Б и С эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием А. | ||
| III | Два равносильных противника играют в шахматы. Что вероятнее: а) выиграть одну партию из двух или две партии из четырех? б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаются. | ||
| IV | В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51. | ||
| V | Монету бросают пять раз. Найти вероятность того, что орел выпадет: а) менее двух раз; б) не менее двух раз. | ||
Задание №5.
Таблица 28
| а) дискретные случайные величины, числовые характеристики дискретных случайных величин | |
| Вариант № | Задание |
| 1 | 2 | |||||
| I | 1.1. Дискретная случайная величина X задана законом распределения X 0,1 0,3 0,6 0,8 P 0,2 0,1 0,4 0,3 Построить многоугольник распределения. 1.2. Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того что тираж содержит пять бракованных книг. 1.3. Для дискретной случайной величины X из п. 1.1. найти: а) математическое ожидание и дисперсию; б) начальные моменты первого, второго и третьего порядков; в) центральные моменты первого, второго, третьего и четвертого порядков. 1.4. Используя неравенство Чебышева, оценить для дискретной случайной величины X из п. 1.1. вероятность того, что │ X-M(X) │< 0,2. | |||||
| II | 1.1. Дискретная случайная величина X задана законом распределения X 0,10 0,15 0,20 0,25 P 0.1 0.3 0.2 0.4 Построить многоугольник распределения. 1.2.Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в момент времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента. 1.3. Для дискретной случайной величины X из п. 1.1. найти: а) математическое ожидание и дисперсию; б) начальные моменты первого, второго и третьего порядков; в) центральные моменты первого, второго, третьего и четвертого порядков. 1.4. Используя неравенство Чебышева, оценить для дискретной случайной величины X из п. 1.1. вероятность того, что │ X-M(X) │< 0,7. | |||||
| III | 1.1. Дискретная случайная величина X задана законом распределения X 0, 2 0,4 0,5 0,6 P 0.3 0.1 0.2 0.4 Построить многоугольник распределения. 1.2. Станок штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди отобранных 200 деталей окажется ровно 4 бракованных. 1.3. Для дискретной случайной величины X из п. 1.1. найти: а) математическое ожидание и дисперсию; б) начальные моменты первого, второго и третьего порядков; в) центральные моменты первого, второго, третьего и четвертого порядков. 1.4. Используя неравенство Чебышева, оценить для дискретной случайной величины X из п. 1.1. вероятность того, что │ X-M(X) │< 0,5. | |||||
| IV |
X 0,2 0,6 0,9 1,2 P 0.3 0.1 0.2 0.4 Построить многоугольник распределения. 1.2. Завод направил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятности того, что в пути будет повреждено изделий: а) ровно 3; б) менее трех; в) более трех; г) хотя бы одно. 1.3. Для дискретной случайной величины X из п. 1.1. найти: а) математическое ожидание и дисперсию; б) начальные моменты первого, второго и третьего порядков; в) центральные моменты первого, второго, третьего и четвертого порядков. 1.4. Используя неравенство Чебышева, оценить для дискретной случайной величины X из п. 1.1. вероятность того, что │ X-M(X) │< 0,6. | |||||
| V | 1.1. Дискретная случайная величина X задана законом распределения X 0,3 0,4 0,7 0,10 P 0.4 0.1 0.2 0.3 Построить многоугольник распределения. 1.2. Магазин получил 1000 бутылок минеральной воды. Вероятность того, то бутылка окажется разбитой, равна 0,003. Найти вероятности того, что магазин получит разбитых бутылок: а) ровно 2; б) менее двух; в) более двух; г) хотя бы одну. 1.3. Для дискретной случайной величины X из п. 1.1. найти: а) математическое ожидание и дисперсию; б) начальные моменты первого, второго и третьего порядков; в) центральные моменты первого, второго, третьего и четвертого порядков. 1.4. Используя неравенство Чебышева, оценить для дискретной случайной величины X из п. 1.1. вероятность того, что │ X-M(X) │< 0,1. | |||||
| б) непрерывные случайные величины, числовые характеристики непрерывных случайных величин, распределения непрерывной случайной величины. | ||||||
| I | 1.1. Дана функция распределения непрерывной случайной величины X
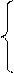 0, x≤0,
F(X)= sin x, 0<x≤Π /2,
1, x>Π/2
Найти плотность распределения f(x).
1.2. Случайная величина X задана плотностью распределения f(x)=2x на интервале (0;1); вне этого интервала f(x)=0. Найти математическое ожидание и дисперсию величины X.
1.3. Случайная величина X задана плотностью распределения f(x)= 0,5x в интервале (0,2), вне этого интервала f(x)=0. Найти начальные и центральные моменты первого, второго, третьего и четвертого порядков.
1.4. Найти дисперсию и среднее квадратическое отклонение случайной величины X, распределенной равномерно в интервале (2,8). 0, x≤0,
F(X)= sin x, 0<x≤Π /2,
1, x>Π/2
Найти плотность распределения f(x).
1.2. Случайная величина X задана плотностью распределения f(x)=2x на интервале (0;1); вне этого интервала f(x)=0. Найти математическое ожидание и дисперсию величины X.
1.3. Случайная величина X задана плотностью распределения f(x)= 0,5x в интервале (0,2), вне этого интервала f(x)=0. Найти начальные и центральные моменты первого, второго, третьего и четвертого порядков.
1.4. Найти дисперсию и среднее квадратическое отклонение случайной величины X, распределенной равномерно в интервале (2,8).
| |||||
| II | 1.1.Дана функция распределения непрерывной случайной величины X
F(X)= sin 2x, 0<x≤Π /4, 1, x>Π/4
Найти плотность распределения f(x). 1.2. Случайная величина X задана плотностью распределения f(x)=(1/2)x на интервале (0;2); вне этого интервала f(x)=0. Найти математическое ожидание и дисперсию величины X. 1.3. Случайная величина X задана плотностью распределения f(x)= 2x в интервале (0,1), вне этого интервала f(x)=0. Найти начальные и центральные моменты первого, второго, третьего и четвертого порядков. 1.4. Случайные величины X и Y независимы и распределены равномерно: x в интервале (a,b), Y –в интервале (c,d). Найти математическое ожидание и дисперсию произведения XY. | |||||
| III | 1.1.Дана функция распределения непрерывной случайной величины X
0, x≤0, F(X)= cos 2x, 0<x≤Π /2, 1, x>Π/2
Найти плотность распределения f(x). 1.4. Случайная величина X задана плотностью распределения f(x) = (-3/4)x 2+(9/2)x-6 на интервале (2; 4); вне этого интервала f(x)=0. Найти моду, математическое ожидание, дисперсию и медиану величины X. 1.3. Случайная величина X задана плотностью распределения f(x)= 4x в интервале (0,2), вне этого интервала f(x)=0. Найти начальные и центральные моменты первого, второго, третьего и четвертого порядков. 1.4. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 10 и 12. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (10, 14). | |||||
| IV | 1.1.Задана плотность распределения f(x) непрерывной случайной величины X
0, x≤0, f(x) = cos x, 0<x≤Π /2, 1, x>Π/2
Найти функцию распределения F(X). 1.2.Случайная величина X задана плотностью распределения f(x)=(-3/4)x 2+6x-45/4 на интервале (3; 5); вне этого интервала f(x)=0. Найти моду, математическое ожидание, дисперсию и медиану величины X. 1.3. Случайная величина X задана плотностью распределения f(x)= (1/3)x в интервале (0,3), вне этого интервала f(x)=0. Найти начальные и центральные моменты первого, второго, третьего и четвертого порядков.
| |||||
| V |  1.1.Задана плотность распределения f(x) непрерывной случайной величины X
0, x≤0,
f(x) = sin, 0<x≤Π /2,
1, x>Π/2
Найти функцию распределения F(X).
1.2.Случайная величина X задана плотностью распределения
f(x)=(-3/4)x 2+12x-8 на интервале (7; 9); вне этого интервала f(x)=0. Найти моду, математическое ожидание, дисперсию и медиану величины X.
1.3. Случайная величина X задана плотностью распределения f(x)= 1,5x в интервале (0,6), вне этого интервала f(x)=0. Найти начальные и центральные моменты первого, второго, третьего и четвертого порядков.
1.4. Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения X подчинены нормальному закону со средним квадратическим отклонением равным 10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превышающей по абсолютной величине 15 мм. 1.1.Задана плотность распределения f(x) непрерывной случайной величины X
0, x≤0,
f(x) = sin, 0<x≤Π /2,
1, x>Π/2
Найти функцию распределения F(X).
1.2.Случайная величина X задана плотностью распределения
f(x)=(-3/4)x 2+12x-8 на интервале (7; 9); вне этого интервала f(x)=0. Найти моду, математическое ожидание, дисперсию и медиану величины X.
1.3. Случайная величина X задана плотностью распределения f(x)= 1,5x в интервале (0,6), вне этого интервала f(x)=0. Найти начальные и центральные моменты первого, второго, третьего и четвертого порядков.
1.4. Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения X подчинены нормальному закону со средним квадратическим отклонением равным 10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превышающей по абсолютной величине 15 мм.
| |||||
Варианты контрольной работы приведены в табл.29. Номер выполняемого варианта совпадает с порядковым номером студента в списке группы.
Таблица 29
| № | Задание №1 | Задание №2 | Задание №3 | Задание №4 | Задание №5 |
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | в, табл. 18 | №1, а), табл. 21 | I | II | III | ||
| 2 | а, табл. 16 | №1, б), табл. 22 | II | III | IV | ||
| 3 | б, табл. 17 | №1, в), табл. 23 | III | IV | V | ||
| 4 | в, табл. 18 | №2, а), табл. 24 | IV | V | I | ||
| 5 | г, табл. 19 | №2, б), табл. 25 | V | I | I | ||
| 6 | д, табл. 20 | №1, в), табл.23 | II | II | II | ||
| 7 | а, табл. 16 | №2, а), табл. 24 | V | III | IV | ||
| 8 | б, табл. 17 | №1, а), табл. 21 | II |
| V | ||
| 9 | в табл. 18 | №1, б), табл. 22 | III | V | V | ||
| 10 | г табл. 19 | №2, а), табл. 24 | I | IV | II | ||
| 11 | д табл. 20 | №1, в), табл.23 | II | II | III | ||
| 12 | в табл. 18 | №2, а), табл. 24 | III | III | IV | ||
| 13 | а табл. 16 | №2, б), табл. 25 | I | IV | I | ||
| 14 | б, табл. 17 | №1, в), табл.23 | II | V | II | ||
| 15 | б, табл. 17 | №2, а), табл. 24 | III | I | III | ||
| 16 | в табл. 18 | №1, а), табл. 21 | IV | III | IV | ||
| 17 | г табл. 19 | №1, б), табл. 22 | V | II | V | ||
| 18 | д табл. 20 | №2, б), табл. 25 | I | III | IV | ||
| 19 | в табл. 18 | №1, в), табл.23 | III | IV | II | ||
| 20 | г табл. 19 | №1, а), табл. 21 | II | V | III | ||
| 21 | д табл. 20 | №1, б), табл. 22 | III | I | IV | ||
| 22 | в табл. 18 | №1, в), табл.23 | IV | V | V | ||
| 23 | а табл. 16 | №2, а), табл. 24 | V | I | IV | ||
| 24 | б, табл. 17 | №2, б), табл. 25 | I | II | I | ||
| 25 | д табл. 20 | №1, б), табл. 22 | V | III | II |
Список литературы
1. Ермаков, В.И. Общий курс высшей математики для экономистов; Учебник для экон.спец.вузов ./Под ред.Ермакова В.И. -М.:ИНФРА-М,1999.
2. Зайцев М. В., Беляев А.А. Прикладная математика: Сборник задач. Часть I. Учебное пособие. М.: Изд-во МГУК, 1999.
3. Зайцев М. В., Беляев А.А. Прикладная математика: Сборник задач. Часть II. Учебное пособие. М.: Изд-во МГУК, 1999.
4. Гмурман В. Е. Теория вероятностей и математическая статистика. - М.: Высш. шк., 1977.
5. Гнеденко Б. В., Хинчин А. Я. Элементарное введение в теорию вероятностей. - М.: Наука., 1976.
6. Колемаев В. А., Староверов О. В., Турундаевский В. Б. Теория вероятностей и математическая статистика. -М.: Высш. шк., 1991.
7. Матвеев В. И., Сагитов Р. В., Шершнев В. Г. Курс линейного программирования для экономистов: Учебное пособие. - Менеджер., 1998.
Дата: 2018-12-28, просмотров: 420.