Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Привести математическую формулировку двойственной задачи.

Решить двойственную задачу.

Найти решение исходной задачи в последней симплексной таблице двойственной задачи. Дать экономическую интерпретацию результатам.

 

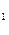Рацион некоторого животного должен в день содержать не менее b1 сумму углеводов и b2 единиц протеина. Для составления рациона имеется три основных вида продуктов. Продукт I стоит - с  за единицу, продукт II – с  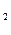за единицу, продукт III - с  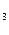за единицу. Продукт I содержит а  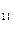единиц углеводов и а  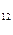единиц протеина. Продукт II содержит а  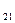единиц углеводов и а  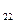 единиц протеина. Продукт III содержит а  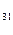единиц углеводов и а  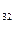единиц протеина. Определить самую дешевую комбинацию продуктов, которая удовлетворит необходимым ограничениям (см. табл. 10).

 

Таблица 10

№ варианта	с	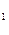с	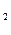с	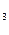b	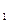b	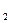а	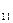а	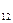а	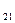а	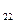а	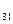a32
I	400	400	500	300	40	600	2	50	8	500	10
II	300	200	400	200	40	200	2	100	4	400	8
III	200	200	300	100	50	400	5	50	2	300	20
IV	100	300	400	300	60	200	4	20	6	250	5
V	200	500	200	150	20	300	6	30	5	300	10

 

Задание 5.

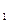Решить задачу  линейного программирования симплексным методом с введением искусственного базиса. Найти максимальное значение функции Z ( X )=с₁+с₂+с₃ при условных: х 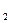, х , х 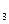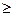0 (см. табл. 11)

Таблица 11

№ варианта

c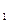

c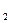

c3

а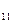

а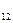

а13

а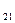

а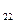

а23

а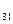

а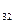

а33

Система ограничений

bi, i=1, 2, 3

 

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
I	2	1	-	5	2	-	2	2	-	0	1	-		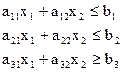30 90 10
II	1	1	-	10	4	-	2	5	-	1	0	-		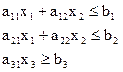20 40 30
III	3	-1	-	3	1	-	1	-1	-	1	0	-		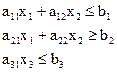30 10 70
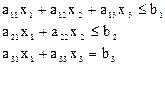
IV	1	1	1	1	2	3	1	3	0	1	0	1	Окончание табл.11	60 10 50
V	-1	-1	5	-1	2	0	1	0	2	0	0	1		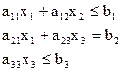50 40 25

 

Задание № 6 . Решить двойственным симплексным методом задачу линейного программирования:

а) Z(X)=-x1- x2-3x3→max x1+ x2+2x3≥1, x1+2x2+x3≥3, 2x1- x2+3x3≥4, x1, x2, x3≥0.	б) Z(X)=-3x1-2 x2-x3→max 2x1+ 2x2≥1, x1+x2+x3≤2, x1+x3≤1, x1, x2, x3≥0.
в) Z(X)=x1+4x2+x3→min x1+ 2x2+3x3≥1, -3x1+x3≤2, -x1- x2+4x3≥1, x1, x2, x3≥0.	г) Z(X)=x1+2x2+4x3→min x1+ x2-x3≥2, 2x1 +2x2+x3≤1, -x1+4 x2+4x3≤3, x1, x2, x3≥0.
д) Z(X)=-x1-2x2-x3→ max x1+ 2x2+3x3≥1, -x1+2x2+x3≤2, 2x1- x2+4x3≥1, x1, x2, x3≥0.

Задание № 7 . Предприятие выпускает 2 вида продукции. Обозначения норм расхода сырья и прибыли от единицы продукции указаны в табл. 12. Численные данные по вариантам приведены в табл. 13.,  дополнительные ограничения даны в табл. 25. Кроме ограничений на сырье имеются статистически обоснованные ограничения на спрос х1 и х2. Восемь вариантов таких ограничений занумерованных римскими цифрами I-VIII и приведены в 1-ом столбце табл. 14. В каждом из вариантов I-VIII имеется три подварианта 1-3 конкретных числовых значений коэффициентов, входящих в эти ограничения. (столбцы 1,2,3 табл. 25.). Всего приведено 25 вариантов задачи о ресурсах.

Таблица 12

Сырье	Расход на единицу продукции		Запасы сырья	Изменения запаса сырья
А	а1	а2	Amax	∆A
В	b1	b2	Bmax	∆B
Прибыль	c1	c2

 

Таблица 13

№

Вариант задания

c1

c2

а1

а2

b1

b2

Amax

Bmax

∆A

∆B

 

1	2	3	4	5	6	7	8	9	10	11	12
1	I,1	3	2	2	1	2	3	10	18	1/2	-2
2	I,2	2	3	4	3	2	1	24	10	-2	2
3	I,3	4	3	3	1	1	3	15	21	3	-3
4	II,1	3	4	1	2	3	2	20	36	2	-1
5	II,2	3	2	3	4	2	1	4	20	-2	3
6	II,3	2	1	1	3	3	1	33	42	-3	3
7	III,1	3	1	2	3	2	1	6	30	-2	4
8	III,2	5	3	3	1	1	1	33	20	1	1
9	III,3	1	1	2	1	1	2	40	44	1	2
10	IV,1	1	2	3	2	1	2	3	15	-2	2
11	IV,2	1	5	1	3	1	1	33	20	3	-3
12	IV,3	1	1	1	2	2	1	2	22	2	-2
13	V,1	6	4	2	1	4	3	10	18	1/2	-2
14	V,2	4	3	8	3	2	2	2	10	-1	2
15	V,3	8	3	6	1	2	3	1	21	30	-1
16	VI,1	6	4	2	2	6	2	2	36	1	-1
17	VI,2	6	2	6	4	4	1	48	20	-1	2
18	VI,3	4	1	2	3	6	1	30	42	-1	1
19	VII,1	6	1	4	3	4	1	60	30	-1	2
20	VII,2	10	3	6	1	2	1	30	20	1	1
21	VII,3	2	1	4	1	2	2	40	44	1	2
22	VIII,1	2	2	6	2	2	2	Окончание табл.13 30	15	-1	3
23	VIII,2	2	5	2	3	2	1	30	20	1	-1
24	VIII,3	2	1	2	2	4	1	20	22	1	1
25	I,1	4	1	2	1	2	3	12	15	1/2	-1/2

 

Таблица 14

		1	2	3
I: x1 ≤ Kx2, x1+x2≤S	K	2	3	4
	S	6.5	6.5	8
II: x2 ≤ Kx1, x1+x2≤S	K	2	3	4
	S	13	13	16
III: x2 ≤ P, x1 ≤x2+∆P	P	18	1	20
	∆P	3	2	5
IV: x1 ≤ Q, x2 ≤x1+∆Q	Q	9	18	10
	∆Q	1.5	4	4
V: 2x1 ≤ Kx2, 2x1+x2≤S	K	2	3	4
	S	6.5	6.5	8
VI: 5x2 ≤ Kx1, 2x1+x2≤S	K	2	3	4
	S	13	13	16
VII: x2 ≤ P, 2x1 ≤x2+∆P	P	18	1	20
	∆P	3	2	5
VIII: 2x1 ≤ Q, x2 ≤2x1+∆Q	Q	9	18	10
	∆Q	1.5	4	4

Выполните следующие задания:

1. В соответствии с порядковым номером полученного вами варианта задания, по первым двум столбцам табл. 13 определите римскую цифру (от до VIII) Вашего варианта дополнительных ограничений и арабскую цифру (от 1 до 3) Вашего подварианта числовых данных в табл. 14.

2.Составьте математическую модель задачи:

1) введите переменные,

2) определите целевую функцию,

3) запишите ограничения на сырье,

4) выпишите дополнительные ограничения на спрос,

5) запишите целиком, полученную модель задачи ЛП,

6) подставьте числовые данные Вашего варианта.

3. Решите полученную задачу ЛП графически или  симплекс-методом.

4. Составьте двойственную задачу ЛП.

 5. Определите двойственные оценки по теореме двойственности. Сравните с индексной строкой последней симплекс-таблицы.

6. Выпишите матрицу устойчивости. Найдите интервалы устойчивости двойственных оценок при изменении каждого сырья в отдельности.

Таблица 15

Варианты контрольной работы приведены в табл.15. Номер выполняемого варианта совпадает с порядковым номером студента в списке группы.

 

№

Задание №1

Задание №2

Задание №3

Задание №4

Задание №5

Задание №6

Задание №7

 

1	2	3	4	5	6	6	7
1	1	№1, табл.5	а	I	IV	а	1
2	2	№1, табл.6	б	II	V	б	2
3	3	№2, табл.7	в	III	I	в	3
4	4	№2, табл.8	г	IV	II	г	4
5	5	№2, табл.9	д	V	III	д	5
6	1	№1, табл.6	в	I	IV	в	6
7	2	№2, табл.7	а	II	V	а	7
8	3	№2, табл.8	б	III	Окончание табл.15 I	б	8
9	4	№1, табл.9	в	IV	III	в	9
10	5	№1, табл.5	г	V	IV	г	10
11	1	№1, табл.6	д	I	V	д	11
12	2	№2, табл.7	а	III	I	б	12
13	3	№2, табл. 9	а	IV	II	а	13
14	4	№2, табл.8	б	V	III	б	14
15	5	№1, табл.5	в	I	IV	в	15
16	1	№1, табл.6	г	II	I	г	16
17	2	№1, табл.5	д	III	III	д	17
18	3	№1, табл.8	г	IV	IV	а	18
19	4	№2, табл.7	а	V	V	а	19
20	5	№2, табл.8	б	II	I	б	20
21	1	№2, табл.7	в	III	II	в	21
22	2	№2, табл.5	г	IV	III	г	22
23	3	№2, табл.7	д	V	IV	д	23
24	4	№1, табл.6	б	I	III	в	24
25	5	№2, табл.9	а	IV	IV	а	25

 

Контрольная работа №2

II. К разделу «Транспортная задача линейного программирования»:

Задание №1