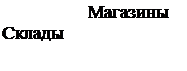Определить вид математической модели задачи.
Задача 1. Малое предприятие (МП) выпускает два вида прохладительных напитков («Радуга» и «Сияние»), предназначенных для детей и взрослых соответственно. В производстве напитков используется 4 вида сырья: газированная вода, фруктовый сироп, лед и тонизирующая добавка. Нормы расхода сырья на производство одной партии напитков и прибыль от ее реализации даны в табл. 1.
Таблица 1
| Сырье | Норма расхода сырья | Суточный запас сырья | |
| «Радуга» | «Сияние» | ||
| Газ. вода | 6 л | 5 л | 1200 л |
| Фруктовый сироп | 1 л | 0,5 л | 150 л |
| Лед | 0,6 кг | 1,2 кг | 150 л |
| Тонизирующая добавка | 0,1 кг | 0,5 кг | 30 кг |
| Прибыль от партии напитка | 30 | 40 | |
Задача 2. Автомобильный завод выпускает три вида автомобилей «Волга»: серийный вариант, повышенной комфортности и представительского класса. Время сборки на конвейере одного автомобиля составляет для этих типов автомобилей 1 мин., 2 мин. и 3 мин., а расход бензина на 100 км равен 10 л,15 л и 20 л соответственно. Экологическое законодательство требует, чтобы средний расход бензина не превышал 13 л. Прибыль от реализации одного автомобиля составляет 6, 10 и 25 тыс. руб. соответственно.
Задача 3. Диетолог разрабатывает новую диету, состоящую из сливочного масла, натуральных бифштексов (мяса), хлеба и яблочного сока. Содержание калорий, белков, жиров, углеводов и холестерина (в 100 г продукта), а также максимальные и минимальные нормы их потребления (в день) приведены в табл. 2. Здесь же указана цена 100 г соответствующего продукта в рублях.
Таблица 2
| Элемент питания | Содержание в 100 г продукта | Норма потребления | ||||
| масло | мясо | хлеб | сок | min | max | |
| Калории | 800 | 280 | 245 | 80 | 2400 | 2800 |
| Белок | 0,6 г | 15 г | 8 г | 0 г | 60 г | 60 г |
| Жир | 20 г | 5 г | 0 г | 0 г | 0 г | 30 г |
| Углеводы | 0 г | 0 г | 5 г | 10 г | 10 г | 40 г |
| Холестерин | 0,15 г | 0,08 г | 0 г | 0 г | 0 г | 0,5 г |
| Цена | 3 | 4 | 0,5 | 1 | ||
Задача 4. Из двух видов сырья завод получает сплав меди, олова и цинка. Процентное содержание компонентов в сырье обоих видов дано в табл. 3.
Таблица 3
| Компоненты | Содержание компонента в сырье | |
| сырье № 1 | сырье № 2 | |
| Медь | 10 % | 25 % |
| Олово | 30 % | 20 % |
| Цинк | 15 % | 10 % |
Цена 1 т сырья составляет 2000 руб. и 3000 руб., а имеющиеся запасы не превышают 5 и 12 т для 1-го и 2-го видов сырья соответственно. Полученный сплав должен содержать не более 1 т цинка, не менее 2 т олова, а содержание в нем меди должно составлять не менее 15 %.
Задача 5. Сельскохозяйственное предприятие обязалось поставить в два магазина 25 и 35 т картофеля соответственно. Предприятие располагает тремя складами с запасами картофеля 15, 20 и 30 т соответственно. Расходы на поставку 1 т картофеля с каждого из складов в оба магазина даны в табл. 4.
Таблица 4
| № 1 | № 2 | |||
| № 1 | 20 | 45 | |||
| № 2 | 30 | 20 | |||
| № 3 | 40 | 35 |
Задание 2.
Составить математическую модель задачи линейного программирования.
Найти графическое линейное решение задачи.
Задача 1. Простейшая диета состоит из телятины и хлеба. Содержание в 100 г продукта калорий и холестерина дано в табл. 5, 6, 7.
Таблица 5
| Элемент питания | Содержание в 100 г продукта | Норма потребления | ||
| телятина | хлеб | min | max | |
| Калории | 600 | 200 | 2400 | 3000 |
| Холестерин | 0,15 | 0,10 | 0 | 0,9 |
| Цена | 3 | 0,5 |
| |
Таблица 6
| Элемент питания | Содержание в 100 г продукта | Норма потребления | ||
| телятина | хлеб | min | max | |
| Калории | 300 | 200 | 2400 | 3600 |
| Холестерин | 0,1 | 0,1 | 0 | 1,5 |
| Цена | 4 | 3 |
| |
Таблица 7
| Элемент питания | Содержание в 100 г продукта | Норма потребления | ||
| телятина | хлеб | min | max | |
| Калории | 350 | 280 | 2100 | 3200 |
| Холестерин | 0,1 | 0,1 | 0 | 1,6 |
| Цена | 5 | 2 |
| |
Задача 2. Цех выпускает два вида смесей из цемента и песка. Процентное содержание цемента и песка в смесях, прибыль от продажи 1 т смеси, запасы цемента и песка и максимальное потребление каждой смеси даны в табл. 8, 9.
Таблица 8
| Компоненты | Смеси | Запасы | |
| № 2 | № 1 | ||
| Цемент | 40 % | 60 % | 9,6 т |
| Песок | 60 % | 40 % | 8,4 т |
| Прибыль | 350 | 480 |
|
| Максимальное потребление | 10 т | 14 т | |
Таблица 9
| Компоненты | Смеси | Запасы | |
| № 2 | № 1 | ||
| Цемент | 20 % | 60 % | 7,2 т |
| Песок | 80 % | 40 % | 12,8 т |
| Прибыль | 320 | 480 |
|
| Максимальное потребление | 14 т | 10 т | |
Задание 3.
Определить вид задачи линейного программирования.
Привести задачу к симплексной форме.
Решите задачу симплекс - методом.
Решить задачу графически.
а) Z(x) = x1+2x2+5→ max
 2x1-x2+5
x1+2x2≤8
x1+x2≤5
x1≥0, x2≥0
| б) Z(x) = 10-6x1-2x2→ min
6x1-2x2≤36
3x1+2x2≤36
x1+2x2≤28
x1≥0, x2≥0
|
| в) Z(x) = x1+3x2+1→ max
-x1+3x2≤9
2x1+3x2≤18
2x1+x2≤14
x1≥0, x2≥0
| г) Z(x) = 2x1+x2+4→ min
-x1+2x2≤4
x1+x2≤5
x1-x2≤3
x1≥0, x2≥0
|
|
д) Z(x) = 3x1+2x2+4→ max
-2x1+3x2≤6
x1+x2≤7
x1-2x2≤4
x1≥0, x2≥0
|
Задание 4.
Дата: 2018-12-28, просмотров: 418.
