При анализе электрических цепей в задачах исследования взаимосвязи между переменными токами (напряжениями, мощностями и т.п.) двух каких-то ветвей схемы широко используется теория четырёхполюсников.
Четырёхполюсник – это часть схемы произвольной конфигурации, имеющая две пары зажимов (отсюда и произошло его название), обычно называемые входными и выходными. Примерами четырёхполюсника являются трансформатор, усилитель, потенциометр, линия электропередачи и другие устройства, у которых можно выделить две пары полюсов. В общем случае четырехполюсники можно разделить на активные, в структуру которых входят источники энергии, и пассивные, ветви которых не содержат источников энергии.
Линейный четырёхполюсник полностью характеризуется соотношениями между токами и напряжениями на его входе и выходе. Вид этих соотношений зависит от выбора исходных величин. Мы будем пользоваться так называемыми h-параметрами.
Рис. 5.14.
Схема четырёхполюсника и
полевого транзистора.
Для описания нелинейного четырёхполюсника в приближении малого сигнала можно использовать линейное приближение, но при этом придётся вводить дифференциальные параметры.
Например:
(5.4)
(5.5)
Таким же способом можно описать полевой транзистор. Для h-параметров полевого транзистора и эквивалентной схемы рис. 5.14 получается:
(5.6)
Кстати:
(5.7)
Это коэффициент усиления по току (см. (5.3)).
Рис. 5.15.
Эквивалентная схема полевого транзистора
с эквивалентным генератором тока, описываемого h-параметрами в соответствии с системой уравнений (5.6, 5.7). Минус перед S потому, что при увеличении входного напряжения (например, с –1В до нуля, см. рис 5.10) входной ток IЗИ уменьшается до нуля.
Благодаря очень высокому входному сопротивлению полевого транзистора на эквивалентной схеме входная и выходная цепи разделены. Входной ток определяется только входным напряжением, что соответствует уравнению (5.6). Выходной ток делится на две ветви. В первой (Δ I1) включён генератор тока, равного первому члену (5.7). Минус написан потому, что при увеличении тока затвора, ток стока уменьшается (см. характеристики рис. 5.10).
Ещё раз напомним, что такое описание справедливо лишь в линейном приближении, то есть для малых изменений токов и напряжений. Только тогда h-параметры можно считать постоянными.
Усилители
Усилители – это устройства, предназначенные для усиления сигналов с использованием вентильных элементов (ламп, транзисторов, реле, тиристоров и т.д.).
Усилители бывают разные. Всё определяется задачей, которую он должен выполнять и наличием деталей. Вот некоторые из типов усилителей:
Переменного тока (и / или напряжения).
Постоянного тока (и / или напряжения). Они, кстати, усиливают и переменный.
Узкополосные.
Широкополосные.
Линейные.
Импульсные.
Сверхвысокочастотные (СВЧ).
Усилители мощности.
И так далее…
Усилители могут быть собраны из дискретных деталей или состоять из одной микросхемы, которая содержит в себе от нескольких штук до нескольких сотен деталей.
Усилитель напряжения часто характеризуют коэффициентом усиления, который, вообще говоря, комплексный. Он показывает, как усиливается напряжение на частоте f , и какой сдвиг фаз между входным и выходным сигналами.
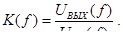(6.1)
Функцию | K( f)| называют амплитудно-частотной или чаще просто частотной характеристикой (ЧХ), а arg K( f) – фазово-частотной или просто фазовой характеристикой. Для учёта нелинейных искажений и определения диапазона линейности усилителя используют зависимость выходного напряжения или же зависимость коэффициента усиления от входного напряжения. Это – амплитудная характеристика.
Ухо человека обладает логарифмической чувствительностью к акустическим волнам. Поэтому иногда коэффициент усиления измеряют в децибелах.
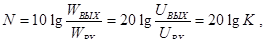(6.2)
где = WВЫХ, WВХ – мощности на выходе и на входе.
Например: К = 100 → N = 40 дБ.
Если в устройстве используется каскад усилителей, то есть несколько усилителей, включённых друг за другом, и они работают в линейном режиме, то их суммарный коэффициент усиления определяется по формулам:
Усилитель с общим эмиттером
Если добавить на рис. 5.6 части А и Б, то получится простейший работоспособный усилитель переменного напряжения. Конденсаторы С1 и С2 отделяют наш усилительный каскад по постоянному напряжению от влияния предыдущего и последующего каскадов. Эти ёмкости определяют низкочастотную часть ЧХ. В практических схемах применяют, конечно, один источник питания, а базовый ток регулируют изменением сопротивления R1.
Для того, чтобы анализировать работу усилительного каскада на рис. 6.1, на графике с выходными характеристиками проводят нагрузочную прямую (рис. 5.5), которая есть график закона Ома для сопротивления RK .
Рис. 6.1.
Схема усилительного каскада с общим эмиттером на биполярном транзисторе. Базовый ток регулируют изменением сопротивления R1.
Усилитель работает на ёмкостную нагрузку СН.
Для того, чтобы провести прямую линию достаточно зафиксировать две точки.
Если предположить, что транзистор VT1 открыт, и напряжение на нём UКЭ = 0, то ток через сопротивление RK , будет IK = E / RK . Это первая точка.
Если транзистор закрыт, то напряжение на RK = 0, и UКЭ = Е. Это – вторая.
Между этими точками мы и провели линию на рис. 5.5.
Пересечения нагрузочной прямой с характеристиками и будут возможными рабочими точками нашего каскада. Например, для тока базы 116 мкА, напряжение на коллекторе транзистора будет +5 В. Рабочая точка характеризуется постоянным напряжением на коллекторе.
Если подать на вход усилителя переменное напряжение, то ток базового перехода будет меняться. Изменение тока коллектора будут в β раз больше. Если изменение тока умножить на сопротивление или импеданс, то мы получим напряжение на выходе схемы.
Рис. 6.2.
Так как биполярный транзистор управляется током базы, то упрощённая эквивалентная схема каскада на рис. 6.1 для переменного тока будет такой.
(β Iб) – это ток коллектора.
На схеме рис. 6.2. СН и RK соединены параллельно потому, что источник питания имеет ничтожно малое сопротивление переменному току. Их импеданс обозначим ZЭКВ.
В учебниках для технических ВУЗов по такой схеме вычисляют коэффициент усиления каскада. Вот пример такого вычисления:
Сумма напряжений по правилу Кирхгофа: тогда:
(6.3)
Учитывая, что и сильно зависят от тока через транзистор (см. рис. 5.4), и их нужно определять экспериментально для каждого экземпляра транзистора, такой расчёт не плодотворен.
Можно воспользоваться экспериментальными выходными характеристиками и определить коэффициент усиления тока. На графике рис. 5.5 между точками φ и θ ток базы изменяется на ΔIБ = 66 мкА, а ток коллектора – на 3 мА. Поделим и получим коэффициент усиления тока KI = 45.
Коэффициент усиления по напряжению по выходным характеристикам можно вычислить, только определив входное сопротивление каскада. Между точками φ и θ напряжение на коллекторе меняется на 3 В, а напряжение на базе на RBX ΔIБ . Если взять, для примера, RBX = 1 кОм, то коэффициент усиления по напряжению KU = ΔUK/ ΔUБ = 45.
Для того, чтобы частотная характеристика усилителя не спадала больше заданной неравномерности частотной характеристики ни на низких, ни на высоких частотах нужно рассчитать величины С1 , С2 и RК .
Рассмотрим входную цепь. Ёмкость C1 вместе с сопротивлением R BX работает как делитель напряжения (вспомните дифференцирующую цепочку) и ослабляет сигналы с частотами ниже fН . Входной ёмкостью транзистора пренебрегаем.
В области низких частот модуль нормированного коэффициента усиления будет:
Если ввести понятие неравномерности частотной характеристики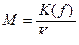 
, то можно выразить, например, нижнюю граничную частоту через неравномерность. Фактически неравномерность – это значение нормированного коэффициента усиления на некоторой частоте.
Если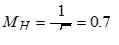 
, то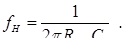 
Для других значений неравномерности значение ёмкости С1 нужно вычислять по формуле:
(6.4)
На Матлабе С1 можно считать так:
clc; % MATLAB ВЫЧИСЛЕНИЕ ЁМКОСТИ С1
M=input('Введи неравномерность MН=');
f=input('Частоту в герцах fН=');
R=input('Входное сопротивление в омах RВХ=');
disp ('Ёмкость '); C1=M/(2*pi*f*R*sqrt(1-M*M))
Таким образом, меняя C1 , можно изменять нижнюю частоту пропускания fH . Манипулируя же частотными зависимостями импедансов в выходной цепи, можно дополнительно управлять частотной зависимостью коэффициента усиления на высоких частотах. Более подробный расчёт транзисторных схем сильно ограничен значительным разбросом параметров транзисторов.
Рассмотрим выходную цепь. Ёмкостная нагрузка нашего усилителя CН шунтирует
сопротивление RK на частотах выше . В результате наличие этой ёмкости
ограничивает сверху полосу работы усилителя. Импеданс RK и CН , включённых параллельно, легко найти:
Так как коэффициент усиления пропорционален ZЭКВ (см. (6.3)), то и неравномерность MB пропорциональна ZЭКВ .
Отсюда (6.5)
Теперь по заданной ёмкости нагрузки, по верхней частоте и неравномерности можно вычислить сопротивление резистора RK .
На Матлабе RK можно сосчитать так:
clc; % MATLAB
% ВЫЧИСЛЕНИЕ СОПРОТИВЛЕНИЯ RК
M=input('Введи неравномерность MВ=');
f=input('Частоту в кГц fВ=');
C=input('Ёмкость нагрузки в пФ СВ=');
disp ('Сопротивление в омах');
Rk=sqrt(1-M*M)/(2*pi*f*C*M*1E-9)
Рис. 6.3.
Экспериментальная частотная характеристика усилителя (ЧХ) в логарифмических координатах. По оси ординат обычно откладывают нормированный на единицу коэффициент усиления
Дата: 2018-12-28, просмотров: 273.
