Метод неопределенных коэффициентов применяется для нахождения частного решения 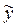 неоднородного уравнения с постоянными коэффициентами в тех случаях, когда функция f(x), стоящая в правой части этого уравнения, имеет один из двух "специальных" видов:
неоднородного уравнения с постоянными коэффициентами в тех случаях, когда функция f(x), стоящая в правой части этого уравнения, имеет один из двух "специальных" видов:
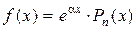 , (42)
, (42)
где Pn(x) – многочлен степени n: Pn(x) = a0 xn + a1 xn –1 +….+ an –1 x + an,
или
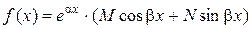 , (43)
, (43)
где M и N – числа.
1) Если 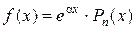 , то частное решение можно искать в виде:
, то частное решение можно искать в виде:
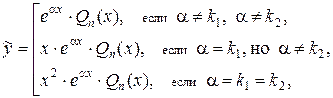 (44)
(44)
где k1, k2 – корни характеристического уравнения, Qn(x) – многочлен степени n, записанный с неопределенными коэффициентами, подлежащими определению, например,
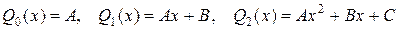 , и т. д.
, и т. д.
2) Если 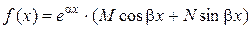 , то частное решение
, то частное решение 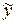 можно искать в виде:
можно искать в виде:
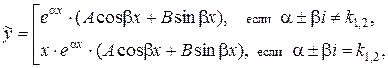 (45)
(45)
где k1, k2 – корни характеристического уравнения, А и В – неизвестные постоянные, подлежащие определению.
Пример 6. Найти общее решение уравнения 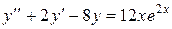 .
.
Решение.
1 этап. Построим общее решение y0 соответствующего однородного уравнения 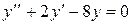 . Составим для него характеристическое уравнение
. Составим для него характеристическое уравнение 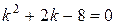 и найдем корни:
и найдем корни: 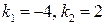 – корни вещественные и различные. По табл. 4 определим вид линейно независимых частных решений однородного уравнения:
– корни вещественные и различные. По табл. 4 определим вид линейно независимых частных решений однородного уравнения: 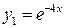 ,
, 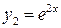 и запишем его общее решение:
и запишем его общее решение:
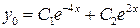 .
.
2 этап. Построим частное решение данного неоднородного уравнения 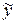 . В заданном уравнении
. В заданном уравнении 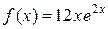 – правая часть 1-го специального вида:
– правая часть 1-го специального вида: 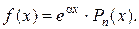 Здесь
Здесь 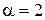 , Pn(x) = 12x, т. е. многочлен в правой части – 1-й степени (n = 1). Число
, Pn(x) = 12x, т. е. многочлен в правой части – 1-й степени (n = 1). Число 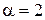 совпадает с одним корнем характеристического уравнения
совпадает с одним корнем характеристического уравнения 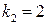 . Следовательно, согласно (44) частное решение
. Следовательно, согласно (44) частное решение 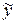 будем искать в виде:
будем искать в виде:
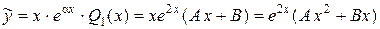 ,
,
где А, B – неизвестные коэффициенты, подлежащие определению.
Найдем производные 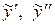 и подставим
и подставим 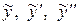 в данное неоднородное уравнение
в данное неоднородное уравнение 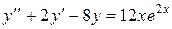 , при этом для простоты используем следующую форму записи:
, при этом для простоты используем следующую форму записи:
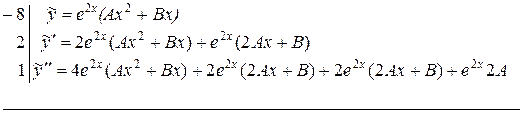
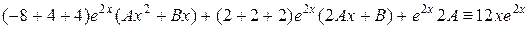 .
.
Здесь слева от черты записаны коэффициенты, с которыми 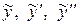 входят в уравнение, а под чертой приравниваются (тождественно) левая
входят в уравнение, а под чертой приравниваются (тождественно) левая
и правая части уравнения после подстановки в него 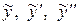 с группировкой подобных членов.
с группировкой подобных членов.
После сокращения обеих частей тождества на 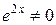 , получаем:
, получаем: 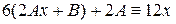 , откуда, приравнивая коэффициенты при х1 и при х0 в обеих частях тождества, получаем:
, откуда, приравнивая коэффициенты при х1 и при х0 в обеих частях тождества, получаем: 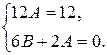
Решая систему, находим 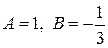 . Подставляя найденные значения в
. Подставляя найденные значения в 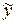 , получим:
, получим: 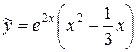 .
.
Объединяя результаты 2-х этапов, получаем общее решение
уравнения:
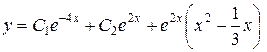 .
.
Ответ: 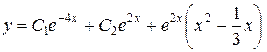 .
.
Пример использования метода неопределенных коэффициентов для случая, когда функция, стоящая в правой части уравнения, имеет 2-й специальный вид, приведен в образце выполнения контрольной работы.
6. Системы двух линейных дифференциальных уравнений
и их решение порядка методом повышения порядка
Нормальная система двух линейных дифференциальных уравнений
1-го порядка имеет вид:
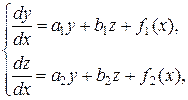 (46)
(46)
где х – независимая переменная, y(x) и z(x) – неизвестные функции, f1(x)
и f2(x) – известные функции a1, a2, b1, b2 – коэффициенты. Общее решение системы (46) имеет вид:
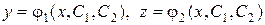 ,
,
где С1 и С2 – произвольные постоянные.
Для решения системы (46) методом повышения порядка необходимо исключить одну из неизвестных функций. Для этого можно выразить одну из функций, например, z(x), из одного уравнения системы:
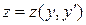 , (47)
, (47)
продифференцировать ее и подставить z и 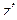 во второе уравнение системы. После упрощения получаем дифференциальное уравнение 2-го порядка вида
во второе уравнение системы. После упрощения получаем дифференциальное уравнение 2-го порядка вида 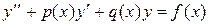 . После получения его решения
. После получения его решения 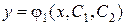 , следует, используя (47), найти вторую неизвестную функцию:
, следует, используя (47), найти вторую неизвестную функцию: 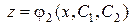 и записать ответ.
и записать ответ.
Если в системе (46) коэффициенты a1, a2, b1, b2 – постоянные, то в результате применения метода повышения порядка получается линейное неоднородное уравнение с постоянными коэффициентами:
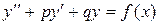 ,
,
решение которого рассмотрено в п. 5.
Пример использования метода повышения порядка для решения системы двух линейных дифференциальных уравнений 1-го порядка приведен в образце выполнения контрольной работы.
Примерный вариант и образец выполнения
контрольной работы 6
Задача 1. Дано дифференциальное уравнение 1-го порядка: 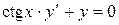 и точка
и точка 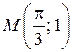 . Определить тип дифференциального уравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М и уравнения еще 4-х интегральных кривых (любых). Построить все эти кривые в системе координат.
. Определить тип дифференциального уравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М и уравнения еще 4-х интегральных кривых (любых). Построить все эти кривые в системе координат.
Задача 2. Дано дифференциальное уравнение 1-го порядка: 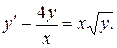 Определить тип дифференциального уравнения и найти его общее решение.
Определить тип дифференциального уравнения и найти его общее решение.
Задача 3. Дано дифференциальное уравнение 2-го порядка: 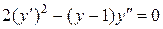 и начальные условия:
и начальные условия: 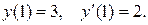 Определить тип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям.
Определить тип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям.
Задача 4. Дано дифференциальное уравнение 2-го порядка: 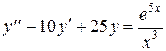 . Определить тип дифференциального уравнения
. Определить тип дифференциального уравнения
и найти его общее решение, используя метод вариации произвольных постоянных.
Задача 5. Дано дифференциальное уравнение 2-го порядка: 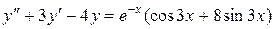 . Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов.
. Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов.
Задача 6. Дана система линейных дифференциальных уравнений 1-го порядка: 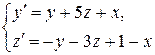 . Найти общее решение системы методом повышения порядка.
. Найти общее решение системы методом повышения порядка.
Решение задачи 1
Данное дифференциальное уравнение 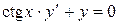 – уравнение
– уравнение
с разделяющимися переменными. Заменим 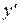 на
на 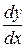 и разделим переменные, умножая обе части уравнения на
и разделим переменные, умножая обе части уравнения на 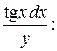
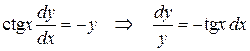 .
.
Интегрируя полученное равенство, получим:
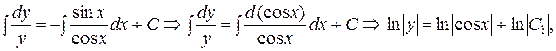
откуда 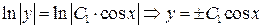 . Заменяя
. Заменяя 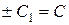 , запишем общее решение данного уравнения:
, запишем общее решение данного уравнения: 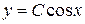 .
.
Найдем уравнение интегральной кривой, проходящей через точку 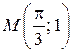 , т. е. частное решение, удовлетворяющее заданному начальному условию:
, т. е. частное решение, удовлетворяющее заданному начальному условию: 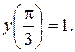 Для этого подставим в общее решение вместо x, y числа
Для этого подставим в общее решение вместо x, y числа 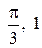 соответственно:
соответственно: 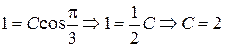 . Подставляя найденное значение С в общее решение, получим искомое частное решение (уравнение интегральной кривой, проходящей через точку М):
. Подставляя найденное значение С в общее решение, получим искомое частное решение (уравнение интегральной кривой, проходящей через точку М): 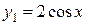 .
.
Найдем уравнения еще нескольких интегральных кривых.
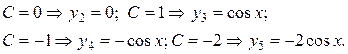
 Построим все эти кривые
Построим все эти кривые
в системе координат (рис. 9).
Ответы: 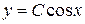 ;
;
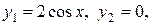
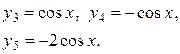
Интегральные кривые изображены на рис. 9.
Решение задачи 2
Данное дифференциальное уравнение 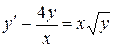 – это уравнение Бернулли (см. (27)), в котором
– это уравнение Бернулли (см. (27)), в котором 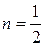 . Применим подстановку
. Применим подстановку 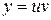 , тогда
, тогда 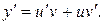 Подставив значения y и
Подставив значения y и 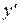 в уравнение, получим
в уравнение, получим 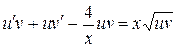 , или
, или
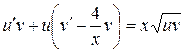 (****)
(****)
Найдем функцию v(x), решая уравнение 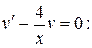
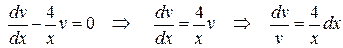 .
.
Проинтегрируем левую и правую части этого уравнения:
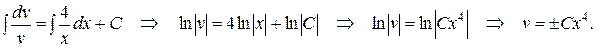
при соответствующем подборе 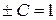 получаем
получаем 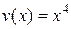 – частное решение уравнения
– частное решение уравнения 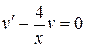 .
.
Подставляя найденную функцию 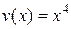
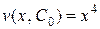 в (****), получим дифференциальное уравнение для функции u:
в (****), получим дифференциальное уравнение для функции u: 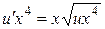 , или
, или 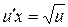 .
.
Найдем функцию 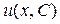 – общее решение этого уравнения:
– общее решение этого уравнения:
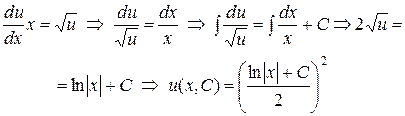
Общим решением исходного уравнения является функция
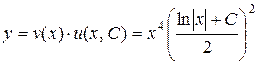 .
.
Ответ: 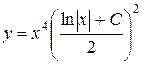 .
.
Решение задачи 3
Данное дифференциальное уравнение 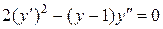 – это дифференциальные уравнения 2-го порядка, не содержащие независимой переменной x (см. (34)). Полагаем
– это дифференциальные уравнения 2-го порядка, не содержащие независимой переменной x (см. (34)). Полагаем 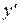 = p(y), тогда
= p(y), тогда 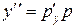 и уравнение примет вид:
и уравнение примет вид:
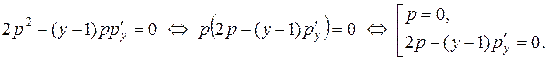
Решая первое уравнение, получим: 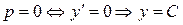 – первое семейство решений. Оно не удовлетворяет начальному условию
– первое семейство решений. Оно не удовлетворяет начальному условию 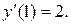
Второе уравнение 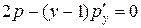 есть уравнение с разделяющимися переменными. Разделим переменные, заменяя
есть уравнение с разделяющимися переменными. Разделим переменные, заменяя 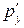 на
на 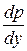 и проинтегрируем:
и проинтегрируем:
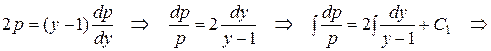
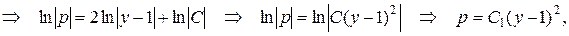
где 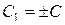 . Производя обратную замену p =
. Производя обратную замену p = 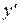 , получим дифференциальное уравнение 1-го порядка относительно неизвестной функции y:
, получим дифференциальное уравнение 1-го порядка относительно неизвестной функции y:
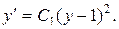
Это уравнение с разделяющимися переменными. Прежде чем его интегрировать, целесообразно определить значение постоянной С1, используя начальные условия (y = 3, 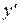 = 2 при х = 1):
= 2 при х = 1):
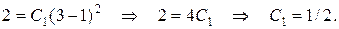
Подставив значение 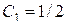 в дифференциальное уравнение, получим:
в дифференциальное уравнение, получим:
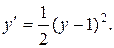
Разделяя переменные и интегрируя, найдем
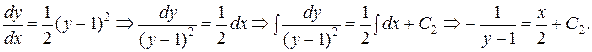
Здесь использовано: 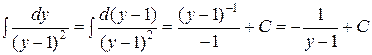 .
.
Определим значение постоянной С2, соответствующее начальному условию y(1) = 3: 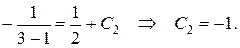
Отсюда получим частный интеграл, удовлетворяющий заданным начальным условиям (решение задачи Коши): 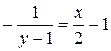 .
.
Получим частное решение уравнения, выразив y(x):
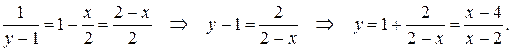
Ответ: 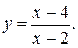
Решение задачи 4
Данное дифференциальное уравнение 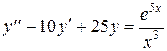 – это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами (см. (38)). Его общее решение имеет вид
– это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами (см. (38)). Его общее решение имеет вид 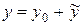 Найдем его в 2 этапа (см. п. 5.3.).
Найдем его в 2 этапа (см. п. 5.3.).
1 этап. Построим общее решение y0 соответствующего однородного уравнения 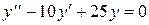 . Составим для него характеристическое уравнение
. Составим для него характеристическое уравнение 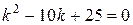 и найдем его корни:
и найдем его корни: 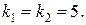 По табл. 4 определим вид его общего решения
По табл. 4 определим вид его общего решения 
2 этап. Построим частное решение 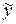 данного неоднородного уравнения при помощи метода вариации произвольных постоянных. Здесь
данного неоднородного уравнения при помощи метода вариации произвольных постоянных. Здесь 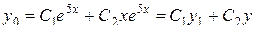 , т. е.
, т. е. 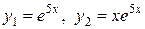 , тогда частное решение
, тогда частное решение 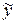 будем искать в виде
будем искать в виде 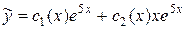 .
.
Составим условиям вариации согласно (40):
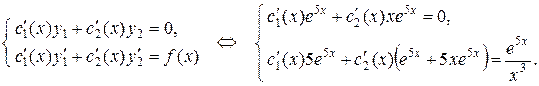
Поделив оба уравнения почленно на 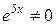 , получим систему с неизвестными
, получим систему с неизвестными 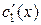 и
и 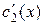 :
:
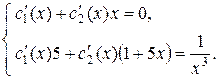
Для решения этой системы можно использовать метод исключения. Выразим 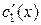 из первого уравнения и подставим во второе:
из первого уравнения и подставим во второе:
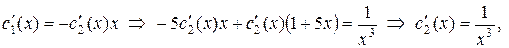
затем найдем 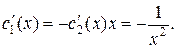
Переходим к интегрированию:
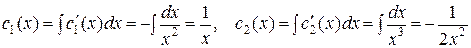
(константы интегрирования считаем равными нулю).
Тогда 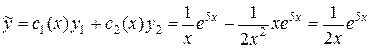 , и общее решение
, и общее решение
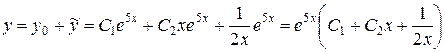 .
.
Ответ: 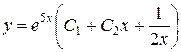 .
.
Решение задачи 5
Данное дифференциальное уравнение 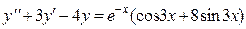 – это линейное неоднородное дифференциальное уравнение 2-го порядка
– это линейное неоднородное дифференциальное уравнение 2-го порядка
с постоянными коэффициентами (см. (38)). Его общее решение имеет вид 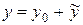 Найдем его в 2 этапа.
Найдем его в 2 этапа.
1 этап. Построим общее решение y0 соответствующего однородного уравнения 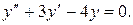 Составим для него характеристическое уравнение
Составим для него характеристическое уравнение 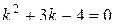 и найдем его корни:
и найдем его корни: 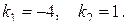 По табл. 4 определим вид его общего решения
По табл. 4 определим вид его общего решения 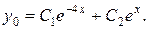
2 этап. Построим частное решение 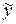 данного неоднородного уравнения при помощи метода неопределенных коэффициентов. В заданном уравнении
данного неоднородного уравнения при помощи метода неопределенных коэффициентов. В заданном уравнении 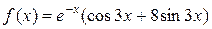 – правая часть 2-го специального вида:
– правая часть 2-го специального вида: 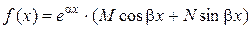 , где
, где 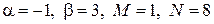 . Числа
. Числа 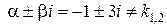 , тогда, согласно (45), частное решение
, тогда, согласно (45), частное решение 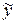 будем искать в виде:
будем искать в виде:
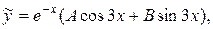
где А и В – неизвестные постоянные. Подставим 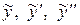 в данное неоднородное уравнение:
в данное неоднородное уравнение:
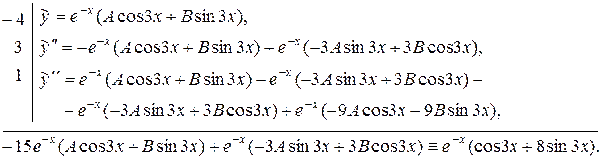
Сократим обе части тождества на 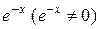 и приравняем коэффициенты при cos3x и при sin3x в левой и правой частях тождества.
и приравняем коэффициенты при cos3x и при sin3x в левой и правой частях тождества.
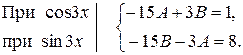
Решая полученную систему двух уравнений с двумя неизвестными, находим 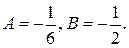 Подставив найденные значения А и В в выражение
Подставив найденные значения А и В в выражение 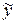 , получим частное решение неоднородного уравнения:
, получим частное решение неоднородного уравнения:
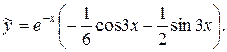
Объединяя результаты 2-х этапов, запишем ответ – общее решение данного уравнения.
Ответ: 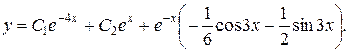
Решение задачи 6
Для решения системы 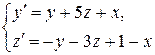 методом повышения порядка исключим из нее одну из функций – z(x).
методом повышения порядка исключим из нее одну из функций – z(x).
Выразим z(x) из первого уравнения системы: 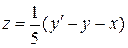 , продифференцируем ее:
, продифференцируем ее: 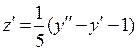 и подставим z и
и подставим z и 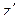 во второе уравнение системы:
во второе уравнение системы:
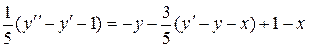 .
.
После упрощения получаем дифференциальное уравнение 2-го порядка относительно функции у(х):
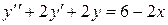 .
.
Это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами (см. (38)). Его общее решение имеет вид 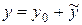 . Найдем его в 2 этапа.
. Найдем его в 2 этапа.
1 этап. Построим общее решение y0 соответствующего одно-
родного уравнения 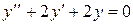 . Составим для него характе-
. Составим для него характе-
ристическое уравнение 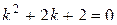 и найдем корни:
и найдем корни: 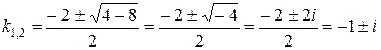 – корни комплексные сопряженные:
– корни комплексные сопряженные: 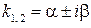 . Здесь
. Здесь 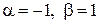 , тогда по таблице 4 определим вид общего решения однородного уравнения:
, тогда по таблице 4 определим вид общего решения однородного уравнения:
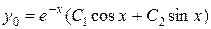 .
.
2 этап. Построим частное решение 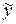 неоднородного уравнения. Здесь
неоднородного уравнения. Здесь 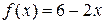 – правая часть 1-го специального вида:
– правая часть 1-го специального вида: 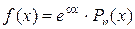 , где
, где 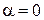 , n = 1. Число
, n = 1. Число 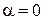 не совпадает с корнями характеристического уравнения
не совпадает с корнями характеристического уравнения 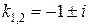 , тогда, согласно (44), частное решение
, тогда, согласно (44), частное решение  будем искать в виде:
будем искать в виде:
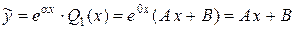 ,
,
где А, B – неизвестные коэффициенты, подлежащие определению.
Найдем производные 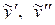 и подставим
и подставим 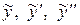 в неоднородное уравнение
в неоднородное уравнение 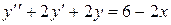 , при этом для простоты используем следующую форму записи:
, при этом для простоты используем следующую форму записи:
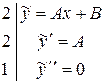
(здесь слева от черты записаны коэффициенты, с которыми 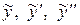 входят в уравнение). Приравниваем левую и правую части уравнения после подстановки в него
входят в уравнение). Приравниваем левую и правую части уравнения после подстановки в него 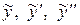 :
:
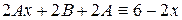 .
.
Приравнивая коэффициенты при х1 и при х0 в обеих частях тождества, получаем:
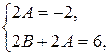
откуда находим: A = –1, B = 4. Подставляя найденные значения в 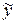 , получим:
, получим: 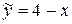 .
.
Объединяя результаты 2-х этапов, получаем общее решение уравнения 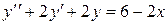 :
:
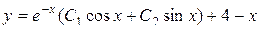 .
.
Найдем вторую неизвестную функцию:
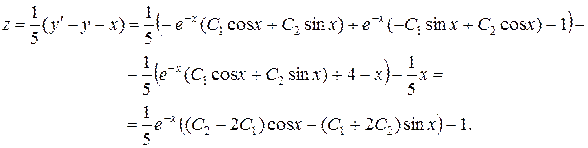
Ответ:
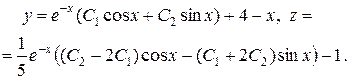
Варианты контрольнЫХ работ
Каждый вариант контрольной работы 5 для студентов-заочников
1 курса всех специальностей содержит 5 задач, охватывающих материал
по теме "Интегральное исчисление функции одной переменной". Каждый вариант контрольной работы 6 содержит 6 задач по теме "Дифференциальные уравнения".
Перед выполнением каждой контрольной работы студенту необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии с методическими указаниями, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задания для всех вариантов общие; студенту следует выбрать из условия каждой задачи данные, необходимые для ее решения, в соответствии со своим вариантом. Оформление контрольных работ должно соответствовать установленным правилам и требованиям. Необходимые чертежи должны выполняться четко, с соответствующими подписями и комментариями (см. образец выполнения примерного варианта работы).
Интегрирование в контрольной работе 5 должно сопровождаться необходимыми ссылками на таблицы интегралов, их свойства, а также указанием метода интегрирования. При использовании замены переменной следует привести формулы замены всех элементов подинтегрального выражения через новую переменную.
Решение всех дифференциальных уравнений в контрольной работе 6 следует приводить подробно, указывая тип уравнения, способ получения решения и используемые методы интегрирования.
Варианты контрольной работы 5
Задача 1. Найти неопределенные интегралы:
| № варианта | Интегралы |
| n | 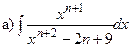 ; ; 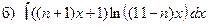 ; ;
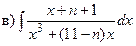 ; ; 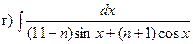
|
В примерах  правильность полученных результатов проверить дифференцированием.
правильность полученных результатов проверить дифференцированием.
Задача 2. Вычислить несобственные интегралы или доказать их расходимость:
| № варианта | Интегралы |
| n | а) 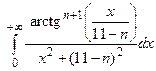 ; б) ; б) 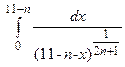
|
Задача 3. Вычислить с помощью определенного интеграла площадь плоской фигуры:
а) ограниченной в ДСК линиями l1 и l2;
б) ограниченной в ПСК линией l.
Сделать чертежи.
| № варианта | ||
Уравнения линий
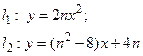
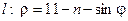
Задача 4. Вычислить с помощью определенного интеграла объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями l1 и l2. Сделать чертеж.
| № варианта | Уравнения линий |
| n | 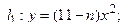 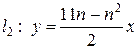
|
Задача 5. Вычислить с помощью определенного интеграла длину дуги кривой, заданной в ДСК уравнением y = f(x), где 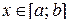 .
.
| № варианта | Уравнение кривой | Промежуток |
| n | 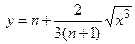
| 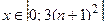
|
Варианты контрольной работы 6
Задача 1. Дано дифференциальное уравнение 1-го порядка и точка М. Определить тип дифференциального уравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М и уравнения еще 4-х интегральных кривых (любых). Построить все эти кривые в системе координат.
| № варианта | Дифференциальное уравнение | Точка |
| 1 | 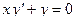
| M(–2; 4) |
| 2 | 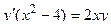
| M(0; 3) |
| 3 | 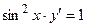
| M 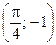
|
| 4 | 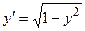
| M(0; 1) |
| 5 | 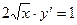
| M(1; 2) |
| 6 | 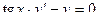
| M 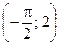
|
| 7 | 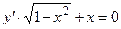
| M(0; –1) |
| 8 | 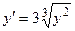
| M(0; 1) |
| 9 | 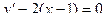
| M(2; 1) |
| 10 | 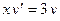
| M(–1; 2) |
Задача 2. Дано дифференциальное уравнение 1-го порядка. Определить тип дифференциального уравнения и найти его общее решение.
| № варианта | Дифференциальное уравнение | № варианта | Дифференциальное уравнение |
| 1 | 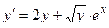
| 6 | 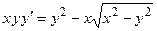
|
| 2 | 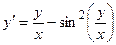
| 7 | 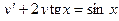
|
| 3 | 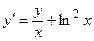
| 8 | 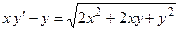
|
| 4 | 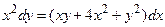
| 9 | 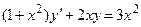
|
| 5 | 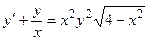
| 10 | 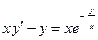
|
Задача 3. Дано дифференциальное уравнение 2-го порядка и начальные условия. Определить тип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям.
| № варианта | Дифференциальное уравнение | Начальные условия |
| 1 | 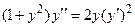
| 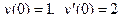
|
| 2 | 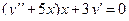
| 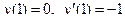
|
| 3 | 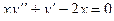
| 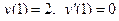
|
| 4 | 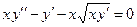
| 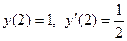
|
| 5 | 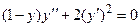
| 
|
| 6 | 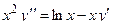
| 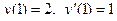
|
| 7 | 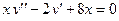
| 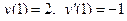
|
| 8 | 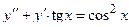
| 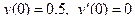
|
| 9 | 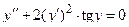
| 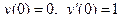
|
| 10 | 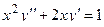
| 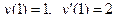
|
Задача 4. Дано дифференциальное уравнение 2-го порядка. Определить тип дифференциального уравнения и найти его общее решение, используя метод вариации произвольных постоянных.
| № варианта | Дифференциальное уравнение | № варианта | Дифференциальное уравнение |
| 1 | 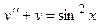
| 6 | 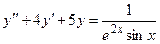
|
| 2 | 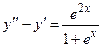
| 7 | 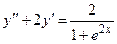
|
| 3 | 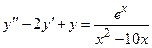
| 8 | 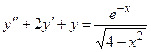
|
| 4 | 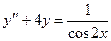
| 9 | 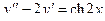
|
| 5 | 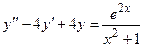
| 10 | 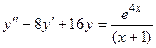
|
Задача 5. Дано дифференциальное уравнение 2-го порядка. Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов.
| № варианта | Дифференциальное уравнение | № варианта | Дифференциальное уравнение |
| 1 | 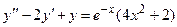
| 6 | 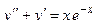
|
| 2 | 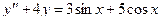
| 7 | 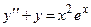
|
| 3 | 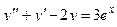
| 8 | 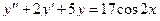
|
| 4 | 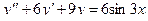
| 9 | 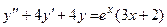
|
| 5 | 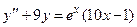
| 10 | 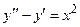
|
Задача 6. Дана система линейных дифференциальных уравнений 1-го порядка. Найти общее решение системы методом повышения порядка.
| № варианта | Система дифференциальных уравнений | № варианта | Система дифференциальных уравнений |
| 1 | 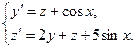
| 6 | 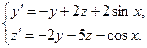
|
| 2 | 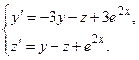
| 7 | 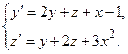
|
| 3 | 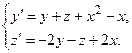
| 8 | 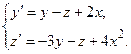
|
| 4 | 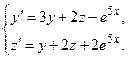
| 9 | 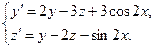
|
| 5 | 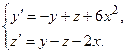
| 10 | 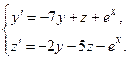
|
Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. – М. : Айрис-пресс, 2003. – 288 с.
2. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 2 / Д.Т. Письменный. – М. : Рольф, 2002. – 256 с.
3. Щипачев, В.С. Высшая математика : учебник для вузов / В.С. Щипачев. – М. : Высш. шк., 1998. – 479 с.
4. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1
/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М. : Высш. шк., 1999. – 304 с.
5. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2
/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М. : Высш. шк., 1999. – 416 с.
6. Щипачев, В.С. Задачник по высшей математике / В.С. Щипачев. – М. : Высш. шк., 2001. – 304 с.
Налоговая льгота – Общероссийский классификатор продукции
ОК 005-93, т. 2; 95 3004 – воспитательная, образовательная и педагогическая литература

Издательство МГТУ. 183010 Мурманск, Спортивная, 13.
Сдано в набор 06.04.2007. Подписано в печать 10.04.2007. Формат 60´841/16
Бум. типографская. Усл. печ. л. 3,02. Уч.-изд. л. 2,36. Заказ 194. Тираж 100 экз.
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ
Федеральное государственное образовательное учреждение высшего профессионального образования
"Мурманский государственный технический университет"
Интегральное исчисление
функции одной переменной.
Дифференциальные уравнения
Часть 3
Мурманск
2007
Дата: 2018-12-28, просмотров: 867.