Дифференциальное уравнение вида
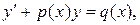 (22)
(22)
где p(x), q(x) – заданные функции, называется линейным дифференциальным уравнением 1-го порядка.
Отличительной особенностью линейного уравнения (22) является
то, что искомая функция y и ее первая производная 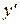 входят в уравнение линейно – в первых степенях и не перемножаются между собой.
входят в уравнение линейно – в первых степенях и не перемножаются между собой.
Для решения уравнения (22) воспользуемся способом подстановки. Будем искать неизвестную функцию y в виде произведения двух тоже пока неизвестных функций: положим y = u(x)v(x). Тогда 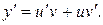 Подставив значения y и
Подставив значения y и 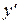 в уравнение (22), получим:
в уравнение (22), получим:
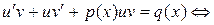
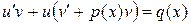 (23)
(23)
Если выбрать v(x) так, чтобы выражение, стоящее в скобках, обратилось в нуль, т. е.
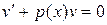 , (24)
, (24)
то для второй функции u(x) из равенства (23) получится уравнение
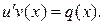 (25)
(25)
Таким образом, решение линейного дифференциального уравнения (22) сводится к решению двух уравнений (24) и (25), каждое из которых является дифференциальным уравнением с разделяющимися переменными. Общее решение уравнения (22) есть произведение какого-либо частного решения уравнения (24) и общего решения уравнения (25):
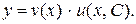 (26)
(26)
Пример 2. Найти решение дифференциального уравнения 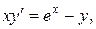
которое удовлетворяет условию 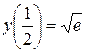 (задача Коши).
(задача Коши).
Решение. Разделив все члены уравнения на х, перепишем уравнение
в виде 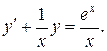 Сравнивая его с уравнением (22), убеждаемся, что оно является линейным дифференциальным уравнением.
Сравнивая его с уравнением (22), убеждаемся, что оно является линейным дифференциальным уравнением.
Положим y = u(x)v(x), тогда 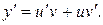 Подставив y и
Подставив y и 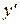 в уравнение, получим:
в уравнение, получим: 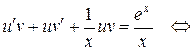
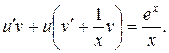 (*)
(*)
Найдем функцию v, решая уравнение 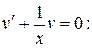
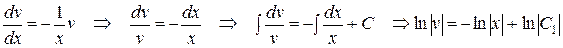
(в данном случае удобно использовать логарифмическую константу интегрирования, положив 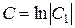 ).
).
Из последнего уравнения следует: 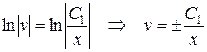 – общее решение, а при соответствующем подборе
– общее решение, а при соответствующем подборе 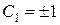 получаем
получаем 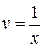 – частное решение уравнения
– частное решение уравнения 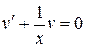 .
.
Подставив найденную функцию 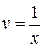 в уравнение (*), получим уравнение для функции u:
в уравнение (*), получим уравнение для функции u: 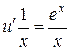 . Найдем функцию
. Найдем функцию 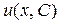 – общее решение этого уравнения:
– общее решение этого уравнения:
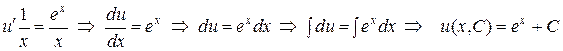 .
.
Общим решением исходного уравнения является функция
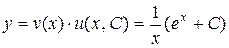 .
.
Найдем частное решение, удовлетворяющее заданному начальному условию 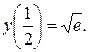 Для этого подставим в общее решение вместо x, y числа
Для этого подставим в общее решение вместо x, y числа 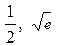 соответственно:
соответственно: 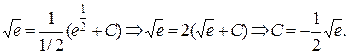
Подставляя найденное значение С в общее решение, получим искомое частное решение (решение задачи Коши): 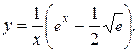
Ответ: 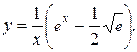
Уравнения Бернулли
Дифференциальное уравнение вида
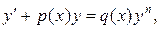 (27)
(27)
где n – действительное число, 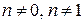 , называется уравнением Бернулли.
, называется уравнением Бернулли.
Уравнение Бернулли является обобщением линейного дифференциального уравнения (22) и может быть решено тем же способом.
Пример решения уравнения Бернулли приведен в образце выполнения контрольной работы.
Однородные уравнения
Функция f(x,y) называется однородной функцией m -го порядка (измерения), если 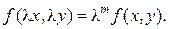
Дифференциальное уравнение вида
P(x, y) dx + Q(x, y) dy = 0 (28)
называется однородным, если P(x, y) и Q(x, y) – однородные функции одного порядка.
Однородное дифференциальное уравнение может быть приведено к виду
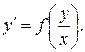 (29)
(29)
С помощью подстановки 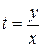 , т. е.
, т. е. 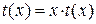 однородное дифференциальное уравнение (29) приводится к уравнению с разделяющимися переменными относительно новой неизвестной функции t(x).
однородное дифференциальное уравнение (29) приводится к уравнению с разделяющимися переменными относительно новой неизвестной функции t(x).
Пример 3. Решить дифференциальное уравнение: 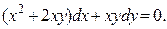
Решение. Здесь 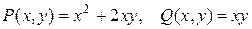 , обе функции – однородные, 2-го порядка, так как выполнено
, обе функции – однородные, 2-го порядка, так как выполнено
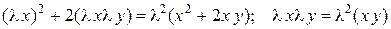 .
.
Разрешим данное уравнение относительно 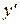 . Для этого запишем его в виде
. Для этого запишем его в виде 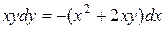 и разделим обе части на xydx, заменяя при этом
и разделим обе части на xydx, заменяя при этом 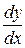 на
на 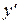 ; в результате получим исходное уравнение в виде (29):
; в результате получим исходное уравнение в виде (29): 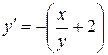 .
.
Введем подстановку y = tx, откуда 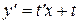 . Тогда уравнение примет вид:
. Тогда уравнение примет вид:
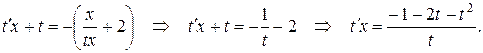
Это дифференциальное уравнение с разделяющимися переменными относительно новой неизвестной функции t(х).
Разделяем переменные t и х:
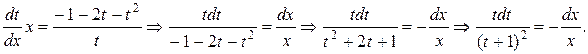
Переходим к интегрированию:
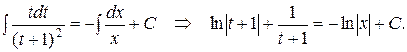
Здесь использовано:
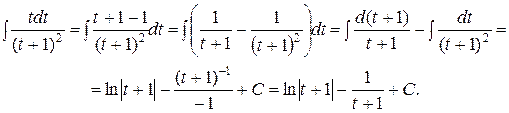
Заменяя t на 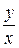 и упрощая результат, получаем:
и упрощая результат, получаем:
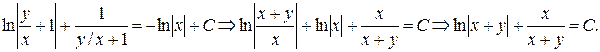
Поскольку функцию y(x) сложно выразить явным образом через х и С, запишем решение в форме общего интеграла уравнения.
Ответ: 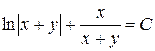 – общий интеграл уравнения.
– общий интеграл уравнения.
Для определения типа дифференциального уравнения 1-го порядка
и выбора метода его решения можно использовать табл. 3.
Таблица 3
| Тип дифференциального уравнения | Вид, к которому приводится уравнение | Метод решения |
| Дифференциальное уравнение с разделяющимися переменными | 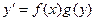
| Разделение переменных:
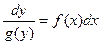
|
| Линейное дифференциальное уравнение 1-го порядка | 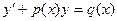
| Замена:
y = u(x)v(x),
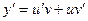
|
| Уравнение Бернулли | 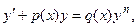
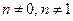
| Замена:
y = u(x)v(x),
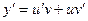
|
| Однородное дифференциальное уравнение 1-го порядка | 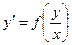
| Замена:
y = tx,
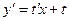 . .
|
Дата: 2018-12-28, просмотров: 350.