Заданная САУ содержит следующие типовые звенья:
- звено W1(p) – инерционное форсирующее;
- звено W2(p) и W3(p) – инерционные;
- звено Woc(p) – пропорциональное.
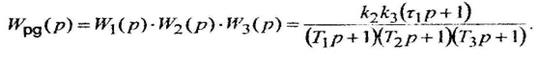
Передаточная функция разомкнутой САУ по задающему воздействию
Передаточная функция разомкнутой САУ по задающему воздействию
Передаточная функция разомкнутой цепи САУ
Передаточная функция замкнутой САУ по задающему воздействию
Передаточная функция замкнутой САУ по возмущающему воздействию
Характеристический полином САУ
 |  | ||
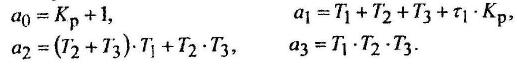Где Кр = к2 к3 кос – коэффициент передачи разомкнутой цепи САУ, а коэффициенты характеристического полинома а0, а1, а2, а3 рассчитываются по выражениям
Определение устойчивости и расчет граничных параметров
 |
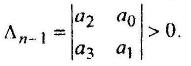В соответствии с критерием Гурвица для устойчивости САУ необходимо, чтобы главный минор определителя Гурвица, составленного из коэффициентов характеристического полинома, был больше нуля, то есть для САУ третьего порядка
 |
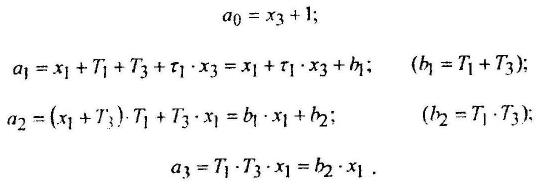Для расчета граничного значения коэффициента передачи разомкнутой цепи и построения области устойчивости для параметров х1 и х2 произведем замену в коэффициентах характеристического полинома фиксированных параметров Кр и Т2 на варьируемые, введя при этом новую переменную х3 = х2 к3 кос = Кp,gr, то есть
 |
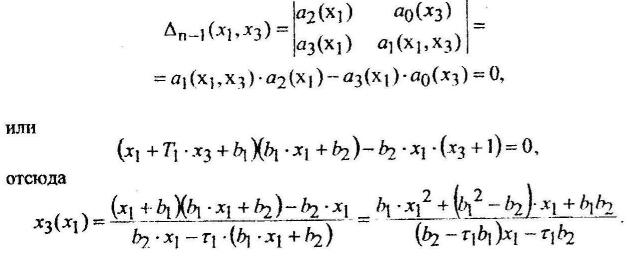Согласно критерию Гурвица, на границе устойчивости главный минор определитель Гурвица равен нулю, то есть требуется решить уравнение.
Полученное выражение отображает границу устойчивости САУ на плоскости параметров х1 и х3. При этом граничное значение Кр = Кр.гр определится как частное решение Кр.гр = х3(Т2), а граница устойчивости в плоскости параметров х1 и х3 находится простым пересчетом по формуле 
и может быть построена путем задания изменения х1 в окрестности постоянной времени Т2.
Ниже приведена часть расчетного файла, реализующая данный пункт задания в пакете MathCad 6.0 Plus. Здесь и далее нумерация коэффициентов передачи, постоянным времени и других параметров выполнена в строку, поскольку в системе MathCad подстрочный индекс соответствует номеру элемента массива.
Исходные данные
k2:=5 k3:=6 koc:=0.6 t1:=0.005 T1:=0.01
T2:=0.4 T3:=0.04 g:=10 f:=5 DG:=8
Коэффициенты характеристического полинома САУ
Kp:=k2 k3 koc
a0:=Kp+1 a1:=T1+T2+T3+Kp t1
a2:=(T2+T3) T1+T2+T3 a3:=T1 T2 T3
Главный минор определителя Гурвица
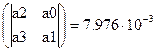
Так как главный минор определителя Гурвица больше нуля, САУ устойчива.
Определение граничного коэффициента передачи разомкнутой цепи
b1:=T1+T3 b2:=T1 T3
Kgr:=x3(T2) Kgr=155.517
Построение границы устойчивости в плоскости параметров х1 и х2
 |
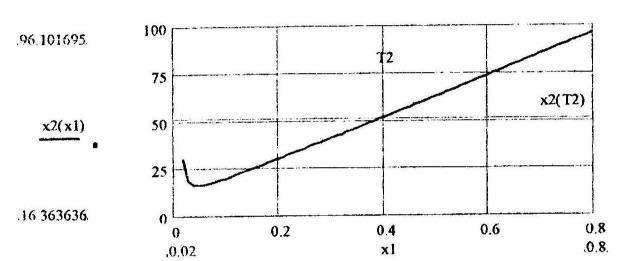х1:=0.03, 0.04..0.8
На приведенном графике значения x1=T2 и x2(T2) показаны посредством маркеров (меток), т.е. установлен флажок в соответствующем пункте графического меню.
Следует отметить, что в некоторых вариантах контрольной работы возможны два решения для границы x2=¦(x1). Они возможны в случае квадратного уравнения вида P(x1)x32+Q(x1)x3+R(x1)=0, где P(x1), Q(x1), R(x1) коэффициенты этого уравнения, зависящие от варьируемого параметра х1. Если одно решение положительно, а второе – отрицательно, то расчет ведется для границы устойчивости, определенной положительным решением. Если оба решения положительны, то учитывается область устойчивости, ограниченная осями координат и кривой, прилегающей к этим осям, а в качестве граничного значения коэффициента передачи в дальнейших расчетах принимается меньшее из полученных решений.
Дата: 2018-12-28, просмотров: 395.
