Введение
Теория автоматического управления (ТАУ) является одной из наиболее важных общетехнических дисциплин, и ее изучение опирается на ряд фундаментальных общеобразовательных и общетехнических дисциплин – математики, информатики, общей электротехники и электроники и т.д.
Целью настоящей курсовой работы является самостоятельное закрепление теоретических знаний по непрерывным линейным системам автоматического управления, полученных на лекциях, практических занятиях и лабораторных работах. Курсовая работа предусматривает самостоятельное выполнение синтеза и анализа следящей САУ. Синтез производится с помощью ЛАЧХ и ЛФЧХ.
Система интегрированного программирования MathCad является хорошим инструментальным средством для решения задач ТАУ. Основы пользования пакетом изучались в курсе «Спец. Главы информатики». При решении задач по курсу ТАУ необходимо знать и использовать дополнительные возможности пакета, как формирование функций из отрезков прямых линий, определение корней линейных алгебраических уравнений, решение трансцендентных уравнений, нанесение на график логарифмической шкалы, интерполяция и математическая регрессия для данных, представленных в виде векторов.
Приобретенные навыки приемов и методов, применяемых при анализе и синтезе систем автоматического управления, будут использованы в изучении дисциплин «Автоматизированный электропривод», «Моделирование систем».
Структурная схема исследуемой системы показана на рис.1.
Рис.1.
В курсовой работе необходимо
1. Определить типовые звенья, входящие в структуру САУ.
2. Определить передаточные функции САУ и ее характеристический полином.
3. По критерию устойчивости Гурвица определить устойчивость САУ, рассчитать граничное значение коэффициента передачи разомкнутой цепи и построить область устойчивости САУ относительно варьируемых параметров Х1 и Х2.
4. Построить статические и внешние характеристики для заданной САУ и для САУ, у которой значение параметра Х2 выбрано в соответствии с заданным запасом устойчивости по амплитуде DG. Рассчитать статизм для обоих вариантов САУ и сравнить полученные результаты.
5. Для САУ, у которой значение параметра Х2 выбрано в соответствии с заданным запасом устойчивости по амплитуде DG, рассчитать асимптотическую и точную ЛАЧХ, точную логарифмическую фазовую частотную характеристику (ЛФЧХ) и определить запас устойчивости по фазе Dj.
6. Для замкнутой САУ, у которой значение параметра Х2 выбрано в соответствии с заданным запасом устойчивости по амплитуде DG, рассчитать амплитудную (АЧХ) и вещественную (ВЧХ) частотные характеристики и определить по ним показатели качества регулирования.
7. Для замкнутой САУ, у которой значение параметра Х2 выбрано в соответствии с заданным запасом устойчивости по амплитуде DG, рассчитать переходные характеристики по задающему g и возмущающему ¦ воздействиями, определить по ним показатели качества регулирования и сравнить результаты с ранее полученными.
8. Исходя из заданного времени переходного процесса tпп и перерегулирования d = 25% провести синтез последовательного корректирующего устройства и рассчитать переходную характеристику скорректированной САУ по задающему воздействию. Определить показатели качества регулирования для этой САУ и сравнить их с ранее рассчитанными.
Курсовая работа выполняется в виде расчетного файла с использованием пакета MathCad. Расчеты необходимо снабжать текстовыми комментариями и выводами.
Вариант курсовой работы выдается преподавателем. Исходные данные для вариантов курсовой работы приведены в приложении П1, а пример ее выполнения в разделе 1.
Пример выполнения курсовой работы.
1.1 Исходные данные к схеме приведены на рис.1.
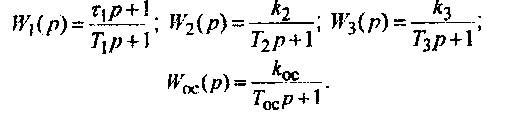
Передаточные функции звеньев САУ
Параметры звеньев и варьируемые параметры приведены в табл.1.
Таблица 1.
| Исходные параметры | Варьируемые параметры | |||||||||||
| k2 | k3 | koc | T1 C | t1 c | T2 c | T3 c | ¦m B | g B | DG дБ | tпп c | x1 | x2 |
| 6 | 5 | 0.6 | 0.01 | 0.005 | 0.4 | 0.04 | 10 | 5 | 8 | 0.04 | T2 | k2 |
Примечание: в табл.1 ¦m – максимальная величина возмущающего воздействия; g – задающее воздействие; DG – запас устойчивости по амплитуде; tпп – время переходного процесса (в секундах).
Исходные данные
k2:=5 k3:=6 koc:=0.6 t1:=0.005 T1:=0.01
T2:=0.4 T3:=0.04 g:=10 f:=5 DG:=8
Коэффициенты характеристического полинома САУ
Kp:=k2 k3 koc
a0:=Kp+1 a1:=T1+T2+T3+Kp t1
a2:=(T2+T3) T1+T2+T3 a3:=T1 T2 T3
Главный минор определителя Гурвица
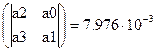
Так как главный минор определителя Гурвица больше нуля, САУ устойчива.
Определение граничного коэффициента передачи разомкнутой цепи
b1:=T1+T3 b2:=T1 T3
Kgr:=x3(T2) Kgr=155.517
Построение границы устойчивости в плоскости параметров х1 и х2
 |
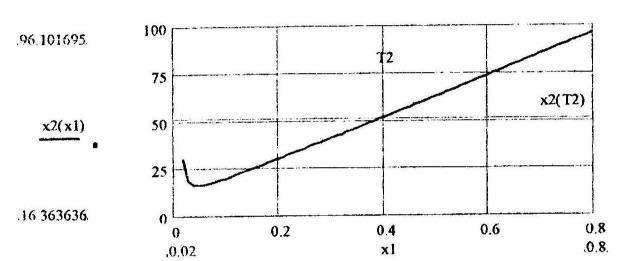х1:=0.03, 0.04..0.8
На приведенном графике значения x1=T2 и x2(T2) показаны посредством маркеров (меток), т.е. установлен флажок в соответствующем пункте графического меню.
Следует отметить, что в некоторых вариантах контрольной работы возможны два решения для границы x2=¦(x1). Они возможны в случае квадратного уравнения вида P(x1)x32+Q(x1)x3+R(x1)=0, где P(x1), Q(x1), R(x1) коэффициенты этого уравнения, зависящие от варьируемого параметра х1. Если одно решение положительно, а второе – отрицательно, то расчет ведется для границы устойчивости, определенной положительным решением. Если оба решения положительны, то учитывается область устойчивости, ограниченная осями координат и кривой, прилегающей к этим осям, а в качестве граничного значения коэффициента передачи в дальнейших расчетах принимается меньшее из полученных решений.
А) установившаяся составляющая
Б) переходная составляющая
 |
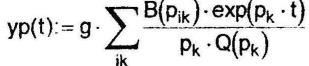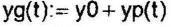В) переходная характеристика
Уравнение переходной характеристики по возмущающему воздействию при t = t0 t0 := 0.1
 |
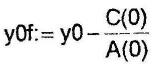А) установившаяся составляющая
 |
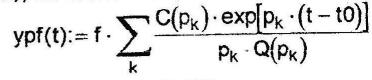Б) переходная составляющая
 |
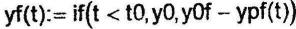В) переходная характеристика
Введение
Теория автоматического управления (ТАУ) является одной из наиболее важных общетехнических дисциплин, и ее изучение опирается на ряд фундаментальных общеобразовательных и общетехнических дисциплин – математики, информатики, общей электротехники и электроники и т.д.
Целью настоящей курсовой работы является самостоятельное закрепление теоретических знаний по непрерывным линейным системам автоматического управления, полученных на лекциях, практических занятиях и лабораторных работах. Курсовая работа предусматривает самостоятельное выполнение синтеза и анализа следящей САУ. Синтез производится с помощью ЛАЧХ и ЛФЧХ.
Система интегрированного программирования MathCad является хорошим инструментальным средством для решения задач ТАУ. Основы пользования пакетом изучались в курсе «Спец. Главы информатики». При решении задач по курсу ТАУ необходимо знать и использовать дополнительные возможности пакета, как формирование функций из отрезков прямых линий, определение корней линейных алгебраических уравнений, решение трансцендентных уравнений, нанесение на график логарифмической шкалы, интерполяция и математическая регрессия для данных, представленных в виде векторов.
Приобретенные навыки приемов и методов, применяемых при анализе и синтезе систем автоматического управления, будут использованы в изучении дисциплин «Автоматизированный электропривод», «Моделирование систем».
Структурная схема исследуемой системы показана на рис.1.
Рис.1.
В курсовой работе необходимо
1. Определить типовые звенья, входящие в структуру САУ.
2. Определить передаточные функции САУ и ее характеристический полином.
3. По критерию устойчивости Гурвица определить устойчивость САУ, рассчитать граничное значение коэффициента передачи разомкнутой цепи и построить область устойчивости САУ относительно варьируемых параметров Х1 и Х2.
4. Построить статические и внешние характеристики для заданной САУ и для САУ, у которой значение параметра Х2 выбрано в соответствии с заданным запасом устойчивости по амплитуде DG. Рассчитать статизм для обоих вариантов САУ и сравнить полученные результаты.
5. Для САУ, у которой значение параметра Х2 выбрано в соответствии с заданным запасом устойчивости по амплитуде DG, рассчитать асимптотическую и точную ЛАЧХ, точную логарифмическую фазовую частотную характеристику (ЛФЧХ) и определить запас устойчивости по фазе Dj.
6. Для замкнутой САУ, у которой значение параметра Х2 выбрано в соответствии с заданным запасом устойчивости по амплитуде DG, рассчитать амплитудную (АЧХ) и вещественную (ВЧХ) частотные характеристики и определить по ним показатели качества регулирования.
7. Для замкнутой САУ, у которой значение параметра Х2 выбрано в соответствии с заданным запасом устойчивости по амплитуде DG, рассчитать переходные характеристики по задающему g и возмущающему ¦ воздействиями, определить по ним показатели качества регулирования и сравнить результаты с ранее полученными.
8. Исходя из заданного времени переходного процесса tпп и перерегулирования d = 25% провести синтез последовательного корректирующего устройства и рассчитать переходную характеристику скорректированной САУ по задающему воздействию. Определить показатели качества регулирования для этой САУ и сравнить их с ранее рассчитанными.
Курсовая работа выполняется в виде расчетного файла с использованием пакета MathCad. Расчеты необходимо снабжать текстовыми комментариями и выводами.
Вариант курсовой работы выдается преподавателем. Исходные данные для вариантов курсовой работы приведены в приложении П1, а пример ее выполнения в разделе 1.
Пример выполнения курсовой работы.
1.1 Исходные данные к схеме приведены на рис.1.
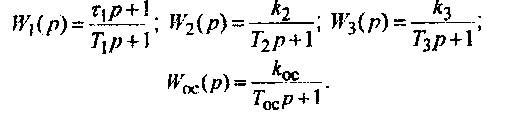
Передаточные функции звеньев САУ
Параметры звеньев и варьируемые параметры приведены в табл.1.
Таблица 1.
| Исходные параметры | Варьируемые параметры | |||||||||||
| k2 | k3 | koc | T1 C | t1 c | T2 c | T3 c | ¦m B | g B | DG дБ | tпп c | x1 | x2 |
| 6 | 5 | 0.6 | 0.01 | 0.005 | 0.4 | 0.04 | 10 | 5 | 8 | 0.04 | T2 | k2 |
Примечание: в табл.1 ¦m – максимальная величина возмущающего воздействия; g – задающее воздействие; DG – запас устойчивости по амплитуде; tпп – время переходного процесса (в секундах).
Дата: 2018-12-28, просмотров: 242.
