Определение 4.10. График функции называется вогнутым (выпуклым вверх) в интервале (а,b), если он расположен выше касательной, проведенной в любой точке этого интервала (Рис. 4.16 ).

Определение 4.11. График функции  называется выпуклым (выпуклым вниз) в интервале (а,b), если он расположен выше касательной, проведенной в любой точке этого интервала (рис. 4.17).

Рис. 4.16                Рис. 4.17                     Рис. 4.18

Теорема. Достаточное условие выпуклости (вогнутости) графика функции. Если  в интервале (а,b), то график функции вогнутый в этом интервале; если же , то в интервале (а,b) график функции — выпуклый.

Определение 4.12. Точка 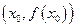 графика функции, отделяющая выпуклую его часть от вогнутой, называется точкой перегиба, причем в этой точке должна существовать единая касательная. (Рис. 4.18).

Если  — абсцисса точки перегиба графика функции , то вторая производная  или  не существует. Точки, в которых  или  не существует, называются критическими точками II рода.

Если х₀ — критическая точка II рода и при переходе через эту точку вторая производная меняет знак, то точка является точкой перегиба. Причем в этой точке функция должна быть непрерывной и должна существовать единая касательная. Если вторая производная не меняет знак, то перегиба в данной точке не будет.

Общая схема исследования функций и построения их графиков

При исследовании функций и построении их графиков реко­мендуется использовать следующую схему.

1. Найти область определения функции.

2. Исследовать функцию на четность — нечетность.

3. Исследовать периодичность функции.

4. Исследовать на непрерывность и поведение функции на концах интервалов определения. Найти вертикальные асимптоты..

5. Исследовать поведение функции при х стремящемся к бесконечности, найти горизонтальные или наклонные асимптоты.

6. Найти экстремумы и интервалы монотонности функции.

7. Найти интервалы выпуклости функции и точки перегиба.

8. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.

9 .Построить график.

10 .Найти область изменения функции.

Заметим, что исследование функции проводится одновременно с построением ее графика.

Пример 4.24. Исследовать функцию  и построить ее график.

Решение.

1. Область определения 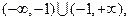 т.е. .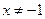

2. Так как 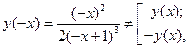 то функция ни четная ни нечетная, т. е. общего вида (график функции несимметричен относительно оси ординат и начала координат).

3. Функция непериодичная.

4. 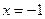 — вертикальная асимптота, так как пределы функции при  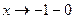(слева) и при  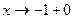(справа) бесконечны, т.е.

.

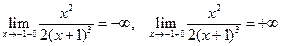5. Наклонные асимптоты находим в ви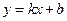де , где

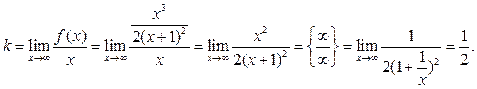
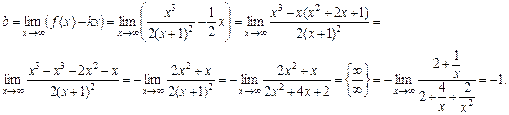
Прямая 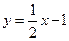 — наклонная асимптота.

6. Экстремумы и интервалы монотонности функции.

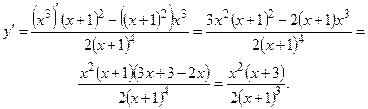
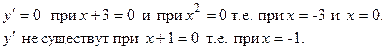
Знаки производной изображены на рисунке.

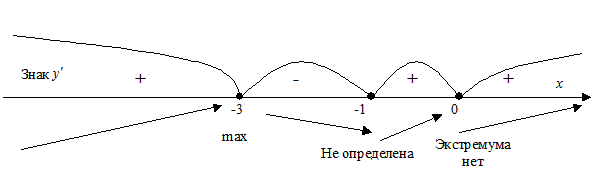
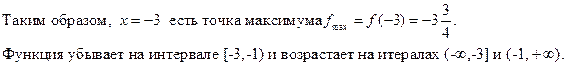
7. Интервалы выпуклости и точки перегиба.

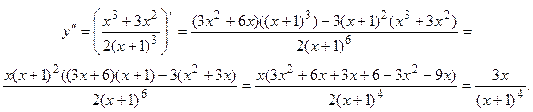
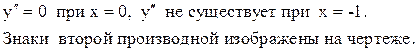
Таким образом, функция вогнута (выпукла вверх) на интегралах (-∞,-1) и (-1,0] и выпукла (выпукла вниз) на интервале[0,∞).

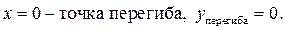
8. f(0)=0. Уравнение f(0)=0 имеет единственное решение х=0, т. е. График функции пересекает оси в начале координат (0,0).

x		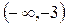-3		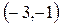-1		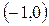0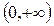
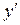
	+	0			+	0	+
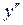
	-	-	-	Ø	-	0	+
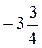
y						0
		max		Не сущ.		Точка перегиба

9. График функции изображен на чертеже.

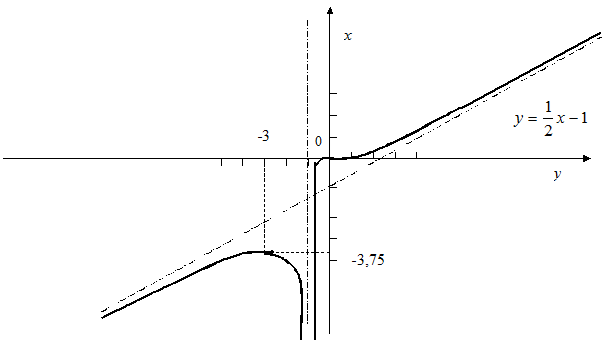
10. Е(у)=(-∞,+∞).