Рассмотрим две произвольные антенны 1 и 2. Считаем, что антенны находятся в дальней зоне относительно друг друга. Поля излучения указанных антенн в передающем режиме могут иметь произвольную поляризацию. Пусть сначала антенна 1 работает в передающем режиме, антенна 2 - в приемном. К входным зажимам антенны 1 подключен генератор с ЭДС 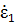 и внутренним сопротивлением Z, к зажимам антенны 2 присоединено сопротивление нагрузки Zн2 (рис. 8, а).
и внутренним сопротивлением Z, к зажимам антенны 2 присоединено сопротивление нагрузки Zн2 (рис. 8, а).
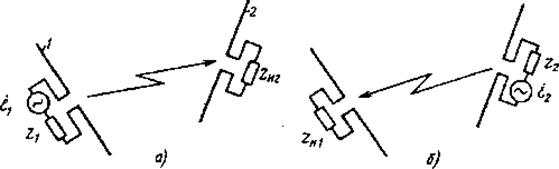
Рисунок 8. Пояснения к применению принципа взаимности для анализа прямоугольных антенн
Под действием ЭДС 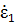 , в антенне 1 возникает ток, величина которого на выходных точках
, в антенне 1 возникает ток, величина которого на выходных точках 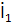 связана с
связана с 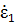 соотношением
соотношением

где 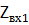 - входное сопротивление антенны 1 в передающем режиме. Электрическое поле, создаваемое антенной 1 и облучающее антенну 2(обозначим его
- входное сопротивление антенны 1 в передающем режиме. Электрическое поле, создаваемое антенной 1 и облучающее антенну 2(обозначим его 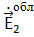 ), может быть в точке расположения антенны 2 представлено как
), может быть в точке расположения антенны 2 представлено как
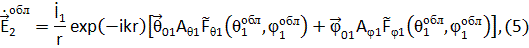
где r - расстояние между антеннами; 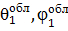 - угловое положение приемной антенны 2 в сферической системе координат r1,
- угловое положение приемной антенны 2 в сферической системе координат r1, 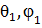 связанной с антенной 1. Под действием
связанной с антенной 1. Под действием 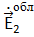 нагрузке приемной антенны 2 возникает ток
нагрузке приемной антенны 2 возникает ток 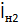 .
.
Хотя нас интересует именно этот ток, поступим далее следующим образом. Сначала из (5) найдем выражение для тока 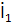 , и подставим его в (4). Получим ЭДС в антенне 1
, и подставим его в (4). Получим ЭДС в антенне 1
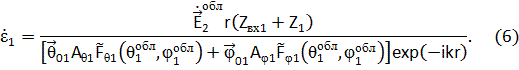
Теперь, не меняя взаимного расположения, изменим режимы работы обеих антенн, подключив ко входным зажимам антенны 2 генератор с ЭДС 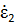 и внутренним сопротивлением Z2, а к зажимам антенны 1 - сопротивление нагрузки Zн1 (рис. 8, б). Ток в нагрузке антенны 1, работающей в приемном режиме, обозначим
и внутренним сопротивлением Z2, а к зажимам антенны 1 - сопротивление нагрузки Zн1 (рис. 8, б). Ток в нагрузке антенны 1, работающей в приемном режиме, обозначим 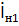 . Проводя рассуждения, аналогичные предыдущему случаю, и используя систему координатr2,
. Проводя рассуждения, аналогичные предыдущему случаю, и используя систему координатr2, 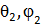 , связанную с антенной 2, получаем ЭДС в антенне 2
, связанную с антенной 2, получаем ЭДС в антенне 2
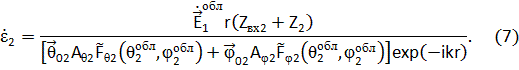
Для нахождения интересующих нас токов 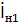 и
и 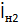 примем, что
примем, что
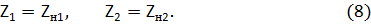
Условие (8) позволяет упростить дальнейший вывод, привлекая формулировку принципа взаимности, известную из теории электрических цепей. Сущность принципа взаимности состоит в следующем. Если к входу линейного пассивного четырехполюсника (рис. 9, а) подключен генератор с ЭДС 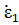 , и внутренним сопротивлением Zн1 , то на его выходе в сопротивлении Zн2 возникает ток
, и внутренним сопротивлением Zн1 , то на его выходе в сопротивлении Zн2 возникает ток 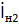 . Если генератор с ЭДС
. Если генератор с ЭДС 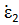 и внутренним сопротивлением Zн2 подключен к выходным зажимам (рис. 9, б), то на входе четырехполюсника в сопротивлении Zн1 появится ток
и внутренним сопротивлением Zн2 подключен к выходным зажимам (рис. 9, б), то на входе четырехполюсника в сопротивлении Zн1 появится ток  . Согласно принципу взаимности
. Согласно принципу взаимности

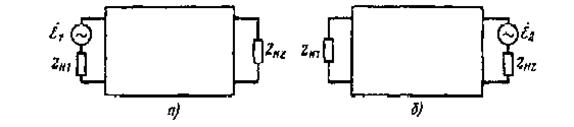
Рисунок 3. Линейный пассивный четырехполюсник
Если среда, окружающая антенны, линейна и изотропна, то зажимы антенн можно принять как зажимы четырехполюсника и использовать соотношение (9), согласно которому, группируя сомножители с индексами 1 и 2, получаем раскрытое выражение (9).
Поскольку антенны являются произвольными, то очевидно, что левая и правая части выражения равны некоторой постоянной С, не зависящей от типа антенн. Из раскрытого выражения, выполнив операцию скалярного умножения векторов, получим соотношение, справедливое для любой приемной антенны:
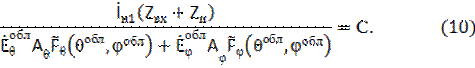
Дата: 2018-11-18, просмотров: 848.