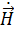Как уже отмечалось, в дальней зоне каждый из векторов  и  в общем случае можно представить в виде суммы двух пространственных компонент:  

Направленные (полевые) параметры антенн. Комплексную диаграмму направленности можно вводить по отношению как к результирующему полю (независимо, электрическому или магнитному, ввиду их пропорциональности в дальней зоне), так и к его отдельным компонентам. Напомним, что комплексная ДН характеризует зависимость амплитуды и фазы излучаемого поля от угловых координат при неизменном расстоянии r от антенны до точки наблюдения. Соответственно различают амплитудную ДН  и фазовую ДН – . Отметим, что для точного описания фазовой ДН следует указывать, относительно какой конкретно точки, выбранной за начало координат, осуществляется расчет или измерение ДН.

Амплитудная ДН обычно нормируется к максимальному значению этой характеристики, т.е. к значению амплитудной ДН в направлении главного максимума излучения, положение которого определяется угловыми координатами 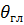, 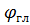. Нормированная амплитудная ДН

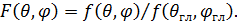                              (15)

Согласно определению амплитудная ДН представляет собой пространственную фигуру, поверхность которой описывается концом радиуса вектора, исходящего из начала координат, длина которого в каждом направлении равна функции . На практике используются как слабонаправленные ДН, например, в форме тороида, соответствующие ДН элементарного электрического вибратора, так и остронаправленные (игольчатой формы), главный лепесток и боковые лепестки, всегда присущие остронаправленной ДН, формируемой реальной антенной ввиду интерференционного характера поля.

Рисунок 4. Форма амплитудной ДН ЭЭВ в плоскостях E и H

Часто ограничиваются амплитудными ДН, изображающими сечения пространственных ДН в каких-либо плоскостях, обычно взаимно перпендикулярных. Для антенн, излучающих линейно-поляризованное поле, такими плоскостями являются плоскости, в которых лежит либо вектор (плоскость Е), либо вектор 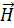 (плоскость H ). На рис. 4 показана форма амплитудной ДН элементарного электрического вибратора в плоскостях E и H. Часто при изображении амплитудных ДН в прямоугольной системе координат используют логарифмический масштаб (в децибелах), вводимый . Логарифмический масштаб позволяет существенно повышать точность изображения боковых лепе стков с малым относительным уровнем. Для примера на рис. 5 приведены сечения остронаправленной ДН в прямоугольной системе координат (в абсолютных единицах и децибелах).

Рисунок 5. Диаграмма направленности в относительных единицах и децибелах

Сечение остронаправленной ДН принято численно характеризовать шириной главного лепестка (шириной луча) и уровнем боковых лепестков (УБЛ). Обычно вводят понятие ширины главного лепестка по уровню нулевого излучения  - угла между направлениями, вдоль которых амплитуда напряженности поля падает до нуля, и ширины главного лепестка по уровню половинной мощности  - угла между направлениями, вдоль которых амплитуда напряженности поля падает до  от максимального значения. Термин «по уровню половинной мощности» связан с тем, что в указанных направлениях плотность потока мощности, пропорциональная квадрату напряженности поля, убывает в 2 раза по сравнению с максимальным значением.

Уровень боковых лепестков ξ характеризуют величиной максимума наибольшего бокового лепестка (обычно ближайшего к главному) по отношению к величине главного максимума. Численно УБЛ равен значению нормированной амплитудной ДН в точках, соответствующих направлению максимума наибольшего бокового лепестка. Иногда важно знать огибающую уровня боковых лепестков.

Знание фазовой ДН 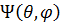 важно, прежде всего для решения вопроса, имеет ли данная антенна фазовый центр. Если  (или меняется скачком на 180° при переходе амплитудной ДН через нуль), то такая антенна имеет фазовый центр в точке, с которой было совмещено начало координат при расчете или измерении фазовой ДН. Поле излучения антенны в этом случае представляет чисто сферическую волну, исходящую из фазового центра. Если , то антенна не имеет фазового центра. Для такой антенны можно подобрать точку, относительно которой фазовая ДН наименее уклоняется от некоторой постоянной величины. Такая точка носит условное название центра излучения антенны.

Поляризационные параметры антенн. Напомним, что под поляризацией поля излучения понимают ориентацию в пространстве вектора . В зависимости от соотношения амплитуд и фаз составляющих поля и  различают линейную, эллиптическую или круговую поляризации. Если компоненты и 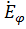 синфазны между собой или их фазы отличаются на , то поляризация поля линейна.Конец вектора  в фиксированной точке пространства с течением времени скользит по прямой, наклон которой в пространстве зависит от соотношения амплитуд компонент и .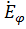

Условием круговой поляризации является равенство амплитуд этих компонент и фазовый сдвиг между ними, равный . В этом случае конец результирующего вектора описывает во времени окружность, причем направление вращения происходит в сторону вектора, запаздывающего по фазе. Различают правое и левое направления вращения. При правом направлении вращение вектора  во времени для наблюдателя, смотрящего вслед волне, происходит по часовой стрелке, при левом направлении - против часовой стрелки.

В общем случае поляризация эллиптическая, т.е. конец результирующего вектора в фиксированной точке пространства описываетв плоскости, перпендикулярной направлению распространения волны и характеризуемой двумя ортогональными координатами x и η, совпадающими с ортами  и , эллипс. Этот эллипс в свою очередь характеризуетсякоэффициентом эллиптичности , где a и b- соответственно малая и большая оси эллипса, направлением вращения и положением большой оси в пространстве (угол , см. рис.6).

Рисунок 6. Эллиптическая поляризация

Таким образом, каждый из видов поляризаций однозначно определяется заданием двух параметров:  - отношением амплитуд ортогональных составляющих поля в данной точке, характеризуемой угловыми координатами, и разностью их фаз, , причем необходимым условием для линейной поляризации является , n=0, 1, 2,..., а для круговой поляризации , разность фаз 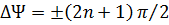,n = 0, 1, 2,… .

Линейная поляризация излучения обычно используется в системах, когда положение передающей и приемной антенн в пространстве не меняется и среда не оказывает существенного влияния на поляризацию поля. Такая ситуация имеет место, например, в наземном телевизионном вещании. При осуществлении связи с подвижными объектами целесообразно использовать круговую поляризацию. В этом случае применяют специальные конструкции антенн, например, турникетные или спиральные.

Для одной и той же антенны вид поляризации излученного поля зависит от направления в точку наблюдения. Зависимость поляризации от направления особенно существенна, если амплитудная ДН не имеет нулей. Доказано, что в этом случае всегда найдется такое направление, где коэффициент эллиптичности s принимает любое наперед заданное значение (от нуля до единицы).

Иногда в антеннах, предназначенных для излучения линейной поляризации поля, возникает паразитное излучение с ортогональной поляризацией за счет неточности изготовления или в силу некоторых конструктивных особенностей. В этом случае различают основную или главную составляющую поляризации поля излучения и кроссполяризационную (вредную) составляющую.

Существуют также системы радиосвязи, в которых каждая из ортогональных поляризаций используется для независимой передачи информации. Для таких систем весьма важен вопрос реализации очень низкого уровня кроссполяризационной составляющей.