Интегрирование рациональных дробей с помощью разложения на простейшие дроби
Под рациональной дробью понимается отношение двух многочленов 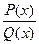 . Рациональную дробь называют правильной, если степень многочлена
. Рациональную дробь называют правильной, если степень многочлена 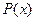 , стоящего в числителе, меньше степени многочлена
, стоящего в числителе, меньше степени многочлена 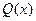 , стоящего в знаменателе.
, стоящего в знаменателе.
Перед интегрированием рациональной дроби 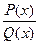 надо сделать следующие алгебраические преобразования и вычисления:
надо сделать следующие алгебраические преобразования и вычисления:
1) если дана неправильная рациональная дробь, то выделить из нее целую часть, т. е. представить в виде
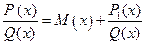 ,
,
где 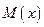 — многочлен, а
— многочлен, а 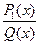 правильная рациональная дробь;
правильная рациональная дробь;
2) разложить знаменатель дроби на линейные и квадратичные множители:
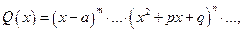
где 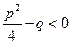 , т.е. трехчлен
, т.е. трехчлен 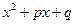 не имеет действительных корней;
не имеет действительных корней;
3) методом неопределенных коэффициентов правильную рациональную дробь разложить на простейшие дроби вида 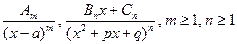 :
:
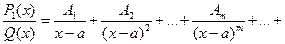
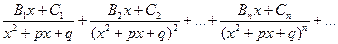
4) вычислить неопределенные коэффициенты 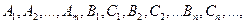 для чего привести последнее равенство к общему знаменателю, приравнять коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить получившуюся систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициенты и другим способом, придавая в полученном тождестве переменной х произвольные числовые значения. Часто бывает полезно комбинировать оба способа вычисления коэффициентов.
для чего привести последнее равенство к общему знаменателю, приравнять коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить получившуюся систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициенты и другим способом, придавая в полученном тождестве переменной х произвольные числовые значения. Часто бывает полезно комбинировать оба способа вычисления коэффициентов.
В результате интегрирование рациональной дроби сведется к нахождению интегралов от многочлена и от простейших рациональных дробей. Простейшие рациональные дроби интегрируются с помощью следующих формул:
1. 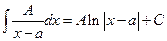 .
.
2. 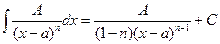 .
.
3. 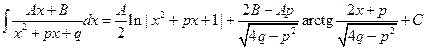 .
.
При интегрировании интегралов третьего вида, как правило, не используют эту формулу, а делают непосредственно преобразования. Такие интегралы можно интегрировать выделением полного квадрата в знаменателе (см. пример 6.2).
Пример 6.16.
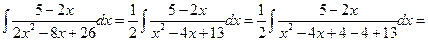
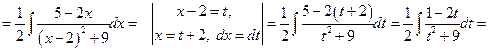
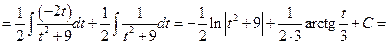
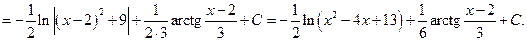
Дроби вида 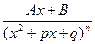 интегрируют, понижая степень знаменателя (см. в справочниках).
интегрируют, понижая степень знаменателя (см. в справочниках).
Пример 6.17. Найти интеграл 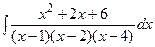 .
.
Решение. Так как каждый из биномов 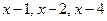 входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде суммы простейших дробей I типа:
входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде суммы простейших дробей I типа:
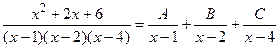 .
. 
Освобождаемся от знаменателя:
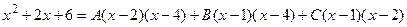 .
.
Следовательно,
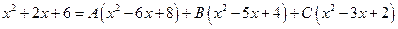 .
.
Сгруппируем члены с одинаковыми степенями:
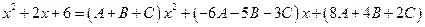 .
.
Сравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений
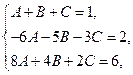
из которой найдем: 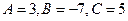 .
.
Итак, разложение рациональной дроби на простейшие имеет вид
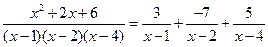 .
.
Неизвестные А, В, С в разложении можно было определить и иначе. После освобождения в равенстве от знаменателя можно придать х столько частных значений, сколько содержится в системе неизвестных, в данном случае три частных значения.
Особенно удобно придавать х значения, являющиеся вещественными корнями знаменателя. Применим этот прием к решению данного примера. После освобождения от знаменателя мы получили
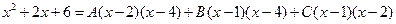 .
.
Действительными корнями знаменателя являются числа 1, 2 и 4. Положим в этом равенстве 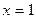 , тогда
, тогда
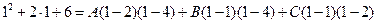 ,
,
откуда 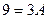 , т. е.
, т. е. 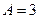 .
.
Полагая 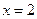 , получаем
, получаем 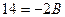 , т. е.
, т. е. 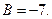
Полагая 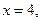 будем иметь
будем иметь  т.е.
т.е. 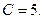
В результате получились те же значения, что и при первом способе определения неизвестных. Таким образом,
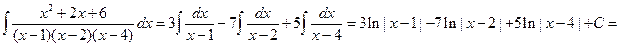
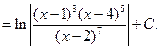
Пример 6.18. Разложение рациональных дробей на простейшие осуществляется по схеме:
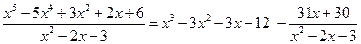 ,
,
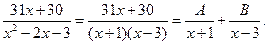
Напишем еще разложение дробей на простейшие без нахождения коэффициентов:
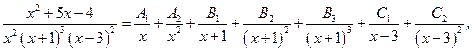
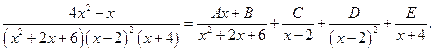
Дата: 2018-11-18, просмотров: 672.