Лекция 13
Первообразная функция. Неопределенный интеграл.
Методы интегрирования.
Вопросы:
1. Первообразная функции и неопределенный интеграл.
2. Основные формулы, используемые при интегрировании.
3. Основные методы интегрирования:
а) Непосредственное интегрирование;
б) Интегрирование методом замены переменной;
в) Интегрирование по частям.
4. Интегрирование рациональных дробей с помощью разложения на простейшие дроби.
5. Интегрирование некоторых видов иррациональностей.
6. Интегрирование тригонометрических функций.
ПОНЯТИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Первообразная функции и неопределенный интеграл
Как известно, математические операции встречаются попарно, образуя пары двух взаимообратных действий. Например, сложение и вычитание, умножение и деление, потенцирование и логарифмирование. При этом прямые действия почти всегда однозначны, а обратные действия чаще всего многозначные.
В предшествующем разделе рассматривалась операция дифференцирования, когда по известной функции  , определялась ее производная. Рассмотрим обратную задачу: по известной функции
, определялась ее производная. Рассмотрим обратную задачу: по известной функции  найти функцию
найти функцию  , что
, что
 . (6.1)
. (6.1)
Определение 6.1. Функция  называется первообразной для функции
называется первообразной для функции  в некотором промежутке
в некотором промежутке  , если в каждой точке этого промежутка выполнено равенство (6.1).
, если в каждой точке этого промежутка выполнено равенство (6.1).
Нахождение первообразной  для данной функции
для данной функции  называют интегрированием. Например, для
называют интегрированием. Например, для  первообразными являются функции
первообразными являются функции  и все функции
и все функции  , где
, где  — произвольная постоянная.
— произвольная постоянная.
Теорема 1. Если  и
и  — две первообразные для функции
— две первообразные для функции  на
на  , то разность между ними равна постоянному числу.
, то разность между ними равна постоянному числу.
Доказательство.  . По следствию из теоремы Лагранжа, если производная функции на некотором отрезке равна нулю, то функция на этом отрезке постоянная. Следовательно, существует число С такое, что
. По следствию из теоремы Лагранжа, если производная функции на некотором отрезке равна нулю, то функция на этом отрезке постоянная. Следовательно, существует число С такое, что  .
.
Отсюда следует, что если для функции  найдена одна первообразная
найдена одна первообразная  , то совокупность всех первообразных для
, то совокупность всех первообразных для  имеет вид
имеет вид  , где
, где  — постоянная величина.
— постоянная величина.

Определение 6.2. Если  является первообразной для
является первообразной для  , то выражение
, то выражение  называется неопределенныминтегралом от функции
называется неопределенныминтегралом от функции  и обозначается символом
и обозначается символом  .
.
Следовательно, по определению
 ,
,
если  .
.
Знак  — символ интеграла, функция
— символ интеграла, функция  — подынтегральная функция,
— подынтегральная функция,  — подынтегральное выражение,
— подынтегральное выражение, 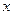 — переменная интегрирования.
— переменная интегрирования.
Теорема 2. Если функция является непрерывной на некотором отрезке, то она интегрируема на этом отрезке.
Таблица неопределенных интегралов
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
7.  .
.
8. 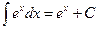 .
.
9.  .
.
10.  .
.
11. 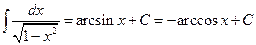 .
.
12.  .
.
13.  .
.
14.  .
.
15.  .
.
16.  .
.
17.  .
.
18.  .
.
19.  .
.
ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
Пример 6.3.
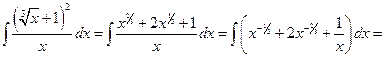
 .
.
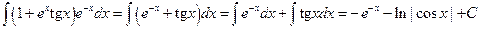 .
.
Часто, при использовании этого метода, эффективен следующий прием.
Пример 6.4.
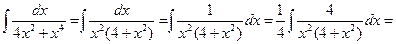
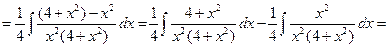

 .
.
Пример 6.5.
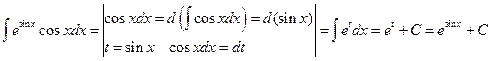 .
.
Пример 6.6.
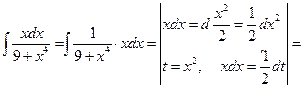
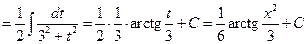 .
.

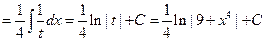 .
.
Пример 6.7.
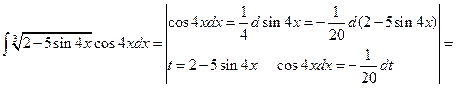
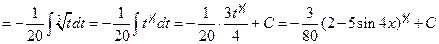 .
.
Следует обратить внимание на то, что после того как найдена первообразная функция 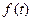 , необходимо произвести обратную замену и вернуться к исходной переменной.
, необходимо произвести обратную замену и вернуться к исходной переменной.
Пример 6.8. Найти интеграл 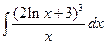 .
.
Решение. Перепишем данный интеграл в виде 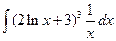 . Производная выражения
. Производная выражения 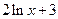 равна 2/х, а второй множитель 1/x отличается от этой производной только постоянным коэффициентом 2. Следовательно,
равна 2/х, а второй множитель 1/x отличается от этой производной только постоянным коэффициентом 2. Следовательно,
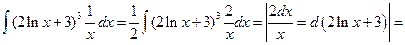
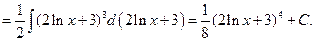
2. Замена переменной в неопределенном интеграле производится также с помощью подстановки вида  , где
, где  — монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае:
— монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае:
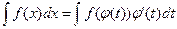 . (6.2)
. (6.2)
Этот метод применяется, если предшествующие два метода не дали результата, замена подбирается таким образом, чтобы появились функции, содержащиеся в таблице основных интегралов.
Докажем эту формулу. Найдем производные левой и правой частей.
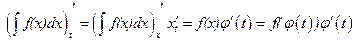 .
.
 .
.
Так как производные равны, то левая и правая части (6.2) по следствию из теоремы Лагранжа отличаются на некоторую постоянную, ч.т.д.
Пример 6.9.
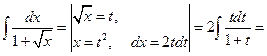
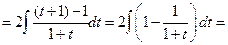
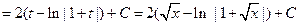 .
.
Пример 6.10. Найти интеграл 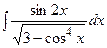 .
.
Решение. Сделаем подстановку  , тогда
, тогда 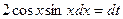 , т.е.
, т.е. 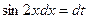 , и
, и  . Тогда
. Тогда
 .
.
Интегрирование по частям
Интегрирование по частям основано на использовании формулы
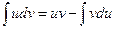 ,
,
где 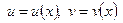 — непрерывно дифференцируемые функции от х на отрезке [а,b].
— непрерывно дифференцируемые функции от х на отрезке [а,b].
Доказательство. Проинтегрируем равенство
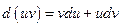 .
.
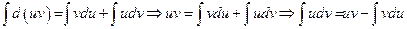 , ч.т.д.
, ч.т.д.
Эта формула дает возможность свести вычисление  к вычислению интеграла
к вычислению интеграла 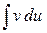 , если он легче интегрируется. При этом за
, если он легче интегрируется. При этом за 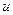 берется такая функция, которая при дифференцировании упрощается, а за dv — та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
берется такая функция, которая при дифференцировании упрощается, а за dv — та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Так, например, для интегралов вида 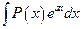 ,
,  ,
, 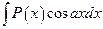 , где
, где 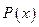 — многочлен, за u следует принять
— многочлен, за u следует принять 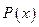 , а за dv — соответственно выражения
, а за dv — соответственно выражения 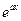 ,
, 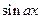 ,
, 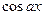 ; для интегралов вида
; для интегралов вида 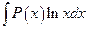 ,
, 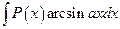 ,
, 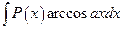 за u принимаются соответственно функции
за u принимаются соответственно функции 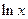 ,
, 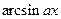 ,
, 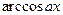 , а за dv — выражение
, а за dv — выражение 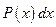 .
.
Пример 6.11. Найти интеграл 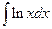 .
.
Решение.
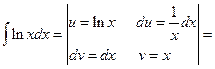
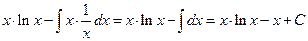 .
.
Пример 6.12. Найти интеграл 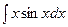 .
.
Решение.
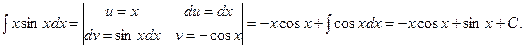
Если бы выражения u и dv мы выбрали иначе, например 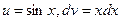 , то получили бы
, то получили бы 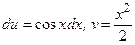 , откуда
, откуда
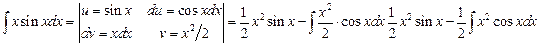
и пришли бы к интегралу более сложному, чем исходный, так как степень сомножителя при тригонометрической функции повысилась на единицу.
Пример 6.13.
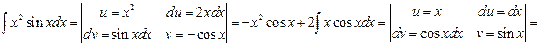
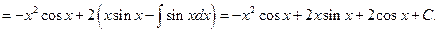
То есть в одном интеграле иногда приходится применять несколько раз этот метод интегрирования.
Пример 6.14.
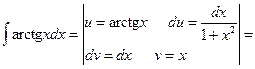
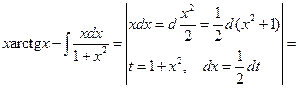
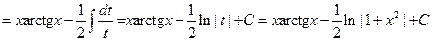 .
.
Пример 6.15.
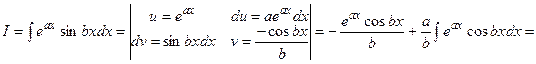

Отсюда 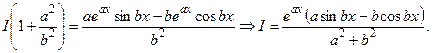
Пример 6.16.

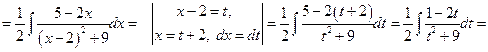
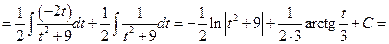
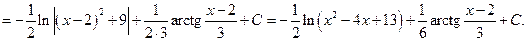
Дроби вида 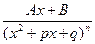 интегрируют, понижая степень знаменателя (см. в справочниках).
интегрируют, понижая степень знаменателя (см. в справочниках).
Пример 6.17. Найти интеграл 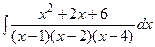 .
.
Решение. Так как каждый из биномов 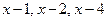 входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде суммы простейших дробей I типа:
входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде суммы простейших дробей I типа:
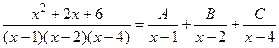 .
. 
Освобождаемся от знаменателя:
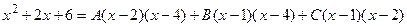 .
.
Следовательно,
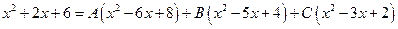 .
.
Сгруппируем члены с одинаковыми степенями:
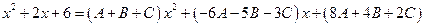 .
.
Сравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений
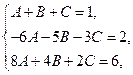
из которой найдем: 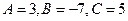 .
.
Итак, разложение рациональной дроби на простейшие имеет вид
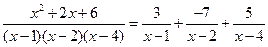 .
.
Неизвестные А, В, С в разложении можно было определить и иначе. После освобождения в равенстве от знаменателя можно придать х столько частных значений, сколько содержится в системе неизвестных, в данном случае три частных значения.
Особенно удобно придавать х значения, являющиеся вещественными корнями знаменателя. Применим этот прием к решению данного примера. После освобождения от знаменателя мы получили
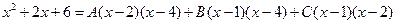 .
.
Действительными корнями знаменателя являются числа 1, 2 и 4. Положим в этом равенстве 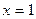 , тогда
, тогда
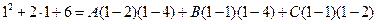 ,
,
откуда 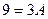 , т. е.
, т. е. 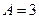 .
.
Полагая 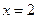 , получаем
, получаем 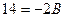 , т. е.
, т. е. 
Полагая 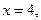 будем иметь
будем иметь  т.е.
т.е. 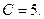
В результате получились те же значения, что и при первом способе определения неизвестных. Таким образом,
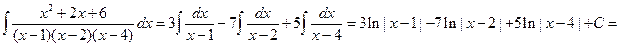
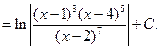
Пример 6.18. Разложение рациональных дробей на простейшие осуществляется по схеме:
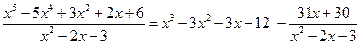 ,
,

Напишем еще разложение дробей на простейшие без нахождения коэффициентов:
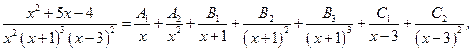
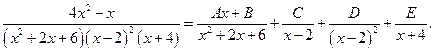
Пример 6.19.
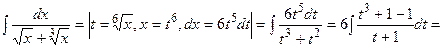

 .
.
2. 
Этот интеграл находится подстановкой  .
.
3. 
4. 
5. 
Пример 6.20.




Проверка:


Пример 6.21.

 .
.
2. Интегрирование произведений синусов и косинусов производится с помощью формул:

Пример 6.22.

3. Интегрирование четных степеней синусов и косинусов производится понижением степени по формулам  .
.
Пример 6.23.


4. Интегрирование нечетных степеней синусов и косинусов производится с помощью замены функции.
Пример 6.24.


Можно использовать следующие подстановки:
 .
.
 .
.
 .
.
Лекция 13
Первообразная функция. Неопределенный интеграл.
Методы интегрирования.
Вопросы:
1. Первообразная функции и неопределенный интеграл.
2. Основные формулы, используемые при интегрировании.
3. Основные методы интегрирования:
а) Непосредственное интегрирование;
б) Интегрирование методом замены переменной;
в) Интегрирование по частям.
4. Интегрирование рациональных дробей с помощью разложения на простейшие дроби.
5. Интегрирование некоторых видов иррациональностей.
6. Интегрирование тригонометрических функций.
Дата: 2018-11-18, просмотров: 608.