Непосредственное интегрирование основано на использовании основных свойств неопределенного интеграла, таблицы интегралов от основных элементарных функций и тождественного преобразования (если необходимо) подынтегральной функции.
1. Используется формула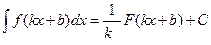 
, т.е. подынтегральная функция отличается от табличной тем, что вместо аргумента 
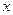стоит некоторая линейная функция от .
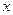Пример 6.1. Найти интеграл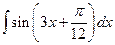 
.
Решение. Здесь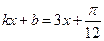 
, следовательно, первообразная будет иметь вид 
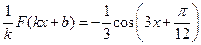и
.
.
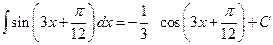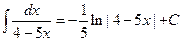Но не всегда применение этой формулы столь очевидно.
Пример 6.2. Найти интеграл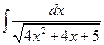 
.
Решение. Подынтегральная функция в этом случае отличается от табличных интегралов, поэтому проведем следующее преобразование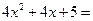 
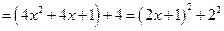. Это действие называется выделением полного квадрата и очень часто при интегрировании выражений, содержащих квадратичный трехчлен, его необходимо использовать. В результате видим, что 
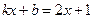и
.
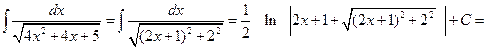
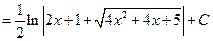2. Используются правила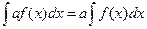 
и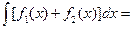 
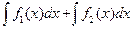. Эти правила применяются в том случае, если подынтегральная функция записана в виде произведения или частного простейших функций. (Правил для интегрирования произведения или частного функций не существует!).
Пример 6.3.
.
.
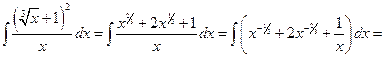
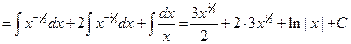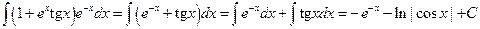Часто, при использовании этого метода, эффективен следующий прием.
Пример 6.4.
.
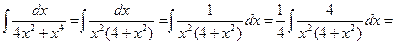
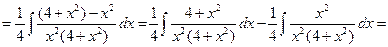
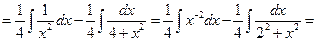
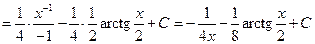Интегрирование методом замены переменной
Замена переменной в неопределенном интеграле производится с помощью подстановок следующих видов.
1. Применяется формула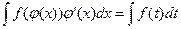 
, которая является аналогом формулы дифференцирования сложной функции. Для выбора новой переменной интегрирования используется определение дифференциала 
.
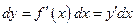Этот метод непосредственного интегрирования имеет свое название — внесение под знак дифференциала.
Пример 6.5.
.
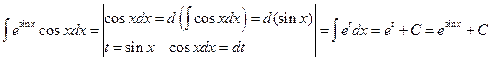Пример 6.6.
.
.
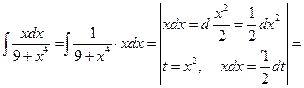
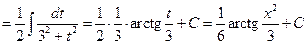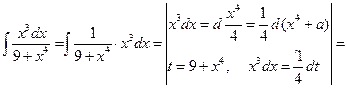
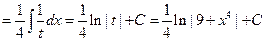Пример 6.7.
.
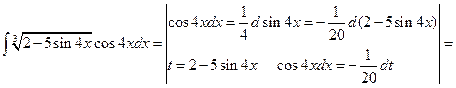
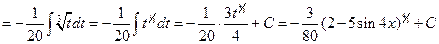Следует обратить внимание на то, что после того как найдена первообразная функция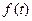 
, необходимо произвести обратную замену и вернуться к исходной переменной.
Пример 6.8. Найти интеграл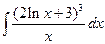 
.
Решение. Перепишем данный интеграл в виде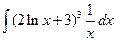 
. Производная выражения 
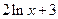равна 2/х, а второй множитель 1/x отличается от этой производной только постоянным коэффициентом 2. Следовательно,
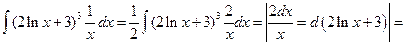
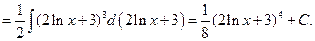
2. Замена переменной в неопределенном интеграле производится также с помощью подстановки вида 
, где 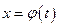— монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае:
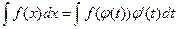. (6.2)
Этот метод применяется, если предшествующие два метода не дали результата, замена подбирается таким образом, чтобы появились функции, содержащиеся в таблице основных интегралов.
Докажем эту формулу. Найдем производные левой и правой частей.
.
.
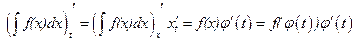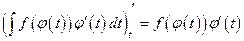Так как производные равны, то левая и правая части (6.2) по следствию из теоремы Лагранжа отличаются на некоторую постоянную, ч.т.д.
Пример 6.9.
.
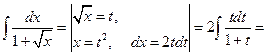
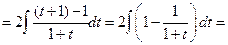
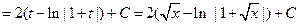Пример 6.10. Найти интеграл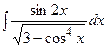 
.
Решение. Сделаем подстановку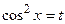 
, тогда 
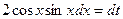, т.е. 
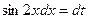, и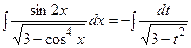 
. Тогда
.
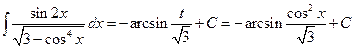Интегрирование по частям
Интегрирование по частям основано на использовании формулы
,
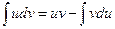где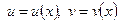 
— непрерывно дифференцируемые функции от х на отрезке [а,b].
Доказательство. Проинтегрируем равенство
.
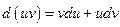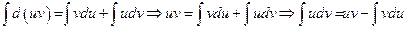, ч.т.д.
Эта формула дает возможность свести вычисление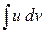 
к вычислению интеграла 
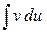, если он легче интегрируется. При этом за 
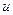берется такая функция, которая при дифференцировании упрощается, а за dv — та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Так, например, для интегралов вида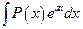 
, 
, 
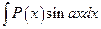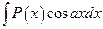, где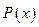 
— многочлен, за u следует принять 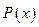, а за dv — соответственно выражения 
, 
, 
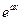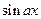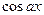; для интегралов вида 
, 
, 
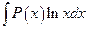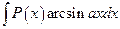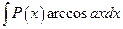за u принимаются соответственно функции 
, 
, 
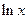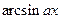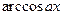, а за dv — выражение 
.
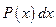Пример 6.11. Найти интеграл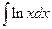 
.
Решение.
.
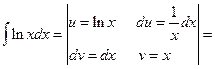
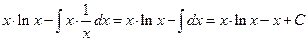Пример 6.12. Найти интеграл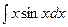 
.
Решение.
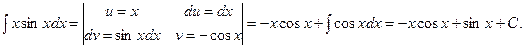
Если бы выражения u и dv мы выбрали иначе, например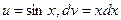 
, то получили бы 
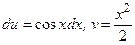, откуда
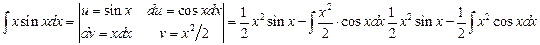
и пришли бы к интегралу более сложному, чем исходный, так как степень сомножителя при тригонометрической функции повысилась на единицу.
Пример 6.13.
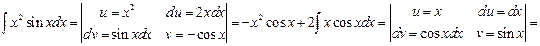
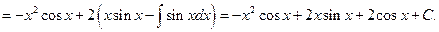
То есть в одном интеграле иногда приходится применять несколько раз этот метод интегрирования.
Пример 6.14.
.
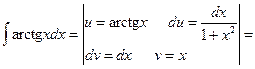
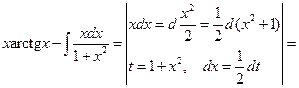
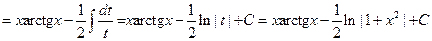Пример 6.15.
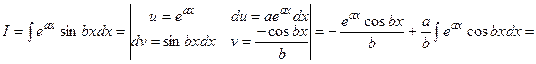
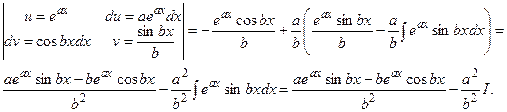
Отсюда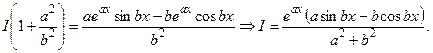 
Дата: 2018-11-18, просмотров: 394.
