Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1. Проранжировать индивидуальные значения первого испытуемого, полученные им в 1-м, 2-м, 3-ми т. д. замерах.

2. Проделать то же самое по отношению ко всем другим испытуемым.

3. Просуммировать ранги по столбцам. Проверить совпадение общей суммы рангов с расчетной сум­мой.

4. Расположить все условия в порядке возрастания их ранговых сумм в таблице.

5. Определить эмпирическое значение L по формуле:

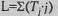
где T_i - сумма рангов по данному условию;

j - порядковый номер, приписанный данному условию в упоря­доченной последовательности условий.

6. Определить критические значения L для данного количества испытуемых n и данного количества условий с. Если L_эмп равен критическому значению или превышает его, тен­денция достоверна.

 

χ ² критерий Пирсона

Назначения критерия

Критерий χ² применяется в двух целях;

1) для сопоставления эмпирического распределения признака с теоре­тическим - равномерным, нормальным или каким-то иным;

2) для сопоставления двух, трех или более эмпирических распределе­ний одного и того же признака[1].

Ограничения критерия

1.    Объем выборки должен быть достаточно большим: п≥30.

2. Теоретическая частота для каждой ячейки таблицы не должна быть меньше 5: f>5. Ес­ли, например, мы хотим проверить наши предположения о том, что частота обращений в телефонную службу Доверия неравномерно распределяются по 7 дням недели, то нам потребуется 5*7=35 обращений. Таким образом, если количество разрядов (k ) задано заранее, как в данном случае, минимальное число наблюдений (n_min) определяется по формуле: n_min=k*5.

3. Выбранные разряды должны "вычерпывать" все распределение, то есть охватывать весь диапазон вариативности признаков. При этом группировка на разряды должна быть одинаковой во всех сопостав­ляемых распределениях.

4. Необходимо вносить "поправку на непрерывность" при сопоставле­нии распределений признаков, которые принимают всего 2 значения. При внесении поправки значение χ² уменьшается.

5. Разряды должны быть неперекрещивающимися: если наблюдение отнесено к одному разряду, то оно уже не может быть отнесено ни к какому другому разряду.

6. Сумма наблюдений по разрядам всегда должна быть равна общему количеству наблюдений.

Расчет критерия χ2 (Пирсон)

1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (первый столбец).

2. Рядом с каждой эмпирической частотой записать теоретическую частоту (второй столбец).

3. Подсчитать разности между эмпирической и теоретической частотой по каждому разряду (строке) и записать их в третий столбец.

4. Определить число степеней свободы по формуле:

ν =κ-1

где κ - количество разрядов признака.

Если ν=1, внести поправку на "непрерывность".

5. Возвести в квадрат полученные разности и занести их в четвертый столбец.

6. Разделить полученные квадраты разностей на теоретическую частоту и записать результаты в пятый столбец.

7. Просуммировать значения пятого столбца. Полученную сумму обозначить как χ²_ЭМП.

8. Определить критические значения для данного числа степеней свободы V.

Если χ²_эмп меньше критического значения, расхождения между распределениями статистически недостоверны.

Если χ²_эмп равно критическому значению или превышает его, расхождения между распределениями статистически достоверны.

λ - критерий Колмогорова-Смирнова

Назначение критерия

Критерий λ предназначен для сопоставления двух распределений:

а) эмпирического с теоретическим, например, равномерным или
нормальным;

б) одного эмпирического распределения с другими эмпирическим
распределением.

Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.

Ограничения критерия λ

1. Критерий требует, чтобы выборка была достаточно большой. При сопоставлении двух эмпирических распределений необходимо, что­бы п1,2 >50. Сопоставление эмпирического распределения с теоре­тическим иногда допускается при п>5.

2. Разряды должны быть упорядочены по нарастанию или убыванию какого-либо признака. Они обязательно должны отражать какое-то однонаправленное его изменение. Например, мы можем за разряды принять дни недели, 1-й, 2-й, 3-й месяцы после прохождения курса терапии, повышение температуры тела, усиление чувства недостаточ­ности и т. д. В то же время, если мы возьмем разряды, которые случайно оказались выстроенными в данную последовательность, то и накопление частот будет отражать лишь этот элемент случайного соседства разрядов. Например, если шесть стимульных картин в ме­тодике Хекхаузена разным испытуемым предъявляются в разном порядке, мы не вправе говорить о накоплении реакций при переходе от картины №1 стандартного набора к картине №2 и т. д. Мы не можем говорить об однонаправленном изменении признака при со­поставлении категорий "очередность рождения", "национальность", "специфика полученного образования" и т.п. Эти данные представ­ляют собой номинативные шкалы: в них нет никакого однозначного однонаправленного изменения признака.

Итак, мы не можем накапливать частоты по разрядам, которые отличаются лишь качественно и не представляют собой шкалы порядка. Во всех тех случаях, когда разряды представляют собой не упо­рядоченные по возрастанию или убыванию какого-либо признака кате­гории, нам следует применять метод χ2.

Расчет абсолютной величины разности d между эмпирическим и равномерным распределениями

1. Занести в таблицу наименования разрядов и соответствующие им
эмпирические частоты (первый столбец).

2. Подсчитать относительные эмпирические частоты (частости) для
каждого разряда по формуле:

f*_эмп=f_эмп/n

где f_эмп - эмпирическая частота по данному разряду;

п - общее количество наблюдений. Занести результаты во второй столбец.

3. Подсчитать накопленные эмпирические частости Σf*j по формуле:

где Σf*j=Σf*_j-1+f*_j - частость, накопленная на предыдущих разрядах; j - порядковый номер разряда; f * _j - эмпирическая частость данного /-го разряда. Занести результаты в третий столбец таблицы.

4. Подсчитать накопленные теоретические частости для каждого раз­
ряда по формуле:

Σf*_{т j}=Σf*_{Т j-1}+f*_{т j} где Σf*_{т j-1} - теоретическая частость, накопленная на предыдущих

разрядах;

j - порядковый номер разряда;

f*_{т j} - теоретическая частость данного разряда. Занести результаты в третий столбец таблицы.

5. Вычислить разности между эмпирическими и теоретическими нако­
пленными частостями по каждому разряду (между значениями 3-го
и 4-го столбцов).

6. Записать в пятый столбец абсолютные величины полученных раз­
ностей, без их знака. Обозначить их как d .

7. Определить по пятому столбцу наибольшую абсолютную величину
разности - d_max.

8. Определить или рассчитать критические
значения d_max для данного количества наблюдений n.

Если d_max равно критическому значению d или превышает его, различия между распределениями достоверны.

Критерий φ* — угловое преобразование Фишера

Назначение критерия φ*

Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта.

Ограничения критерия φ*

1. Ни одна из сопоставляемых долей не должна быть равной нулю. Формально нет препятствий для применения метода φ в случаях, когда доля наблюдений в одной из выборок равна 0. Однако в этих случаях результат может оказаться неоправданно завышенным.

2. Верхний предел в критерии φ отсутствует - выборки могут быть сколь угодно большими.

Нижний предел - 2 наблюдения в одной из выборок. Однако должны соблюдаться следующие соотношения в численности двух выборок:

а) если в одной выборке всего 2 наблюдения, то во второй должно быть не менее 30:

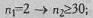
б) если в одной из выборок всего 3 наблюдения, то во второй должно быть не менее 7:

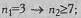
в) если в одной из выборок всего 4 наблюдения, то во второй должно быть не менее 5:

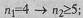
г) при n ₁ , n ₂ ≥5 возможны любые сопоставления.

В принципе возможно и сопоставление выборок, не отвечающих этому условию, например, с соотношением n ₁=2, n ₂⁼15, но в этих слу­чаях не удастся выявить достоверных различий.

Расчет критерия φ*

1. Определить те значения признака, которые будут критерием для разделения испытуемых на тех, у кого "есть эффект" и тех, у кого "нет эффекта". Если признак измерен количественно, использовать критерий λ для поиска опти­мальной точки разделения.

2. Начертить четырехклеточную таблицу из двух столбцов и двух строк. Пер­вый столбец - "есть эффект"; второй столбец - "нет эффекта"; первая стро­ка сверху - 1 группа (выборка); вторая строка - 2 группа (выборка).

3. Подсчитать количество испытуемых в первой группе, у которых "есть эф­фект", и занести это число в левую верхнюю ячейку таблицы.

4. Подсчитать количество испытуемых в первой выборке, у которых "нет эф­фекта", и занести это число в правую верхнюю ячейку таблицы. Подсчитать сумму по двум верхним ячейкам. Она должна совпадать с количеством ис­пытуемых в первой группе.

5. Подсчитать количество испытуемых во второй группе, у которых "есть эф­фект", и занести это число в левую нижнюю ячейку таблицы.

6. Подсчитать количество испытуемых во второй выборке, у которых "нет эф­фекта", и занести это число в правую нижнюю ячейку таблицы. Подсчитать сумму по двум нижним ячейкам. Она должна совпадать с количеством ис­пытуемых во второй группе (выборке).

7. Определить процентные доли испытуемых, у которых "есть эффект", путем отнесения их количества к общему количеству испытуемых в данной группе (выборке). Записать полученные процентные доли соответственно в левой верхней и левой нижней ячейках таблицы в скобках, чтобы не перепутать их с абсолютными значениями.

8. Проверить, не равняется ли одна из сопоставляемых процентных долей ну­лю. Если это так, попробовать изменить это, сдвинув точку разделения групп в ту или иную сторону. Если это невозможно или нежелательно, от­казаться от критерия φ* и использовать критерий χ ².

9. Определить по Табл. XII Приложения 1 величины углов φ для каждой из сопоставляемых процентных долей.

10. Подсчитать эмпирическое значение φ* по формуле:

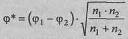
где: φ₁ - угол, соответствующий большей процентной доле;

φ₂ - угол, соответствующий меньшей процентной доле;

n ₁ - количество наблюдений в выборке 1;

n ₂ - количество наблюдений в выборке 2.

11. Сопоставить полученное значение φ* с критическими значениями: φ* ≤1,64 (р<0,05) и φ* ≤2,31 (р<0,01).

Если φ*_эмп ≤φ*_кр. H₀ отвергается.

При необходимости определить точный уровень значимости полученного φ*_эмп по таблице критических значений.

 

Биномиальный критерий m

Назначение критерия m

Критерий предназначен для сопоставления частоты встречаемости какого-либо эффекта с теоретической или заданной частотой его встре­чаемости.

Он применяется в тех случаях, когда обследована лишь одна вы­борка объемом не более 300 наблюдений, в некоторых задачах - не больше 50 наблюдений.