1. Наиболее наглядным видом выбора уравнения парной регрессии является:
а) аналитический;
б) графический;
в) экспериментальный (табличный).
2. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:
а) не менее 5 наблюдений;
б) не менее 7 наблюдений;
в) не менее 10 наблюдений.
3. Суть метода наименьших квадратов состоит в:
а) минимизации суммы остаточных величин;
б) минимизации дисперсии результативного признака;
в) минимизации суммы квадратов остаточных величин.
4. Коэффициент линейного парного уравнения регрессии:
а) показывает среднее изменение результата с изменением фактора на одну единицу;
б) оценивает статистическую значимость уравнения регрессии;
в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.
5. На основании наблюдений за 50 семьями построено уравнение регрессии 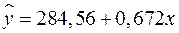 , где
, где 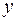 – потребление,
– потребление, 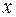 – доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?
– доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?
а) да;
б) нет;
в) ничего определенного сказать нельзя.
6. Суть коэффициента детерминации 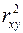 состоит в следующем:
состоит в следующем:
а) оценивает качество модели из относительных отклонений по каждому наблюдению;
б) характеризует долю дисперсии результативного признака 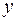 , объясняемую регрессией, в общей дисперсии результативного признака;
, объясняемую регрессией, в общей дисперсии результативного признака;
в) характеризует долю дисперсии 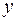 , вызванную влиянием не учтенных в модели факторов.
, вызванную влиянием не учтенных в модели факторов.
7. Качество модели из относительных отклонений по каждому наблюдению оценивает:
а) коэффициент детерминации 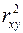 ;
;
б) 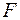 -критерий Фишера;
-критерий Фишера;
в) средняя ошибка аппроксимации 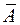 .
.
8. З начимость уравнения регрессии в целом оценивает:
а) 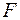 -критерий Фишера;
-критерий Фишера;
б) 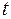 -критерий Стьюдента;
-критерий Стьюдента;
в) коэффициент детерминации 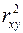 .
.
9. Классический метод к оцениванию параметров регрессии основан на:
а) методе наименьших квадратов:
б) методе максимального правдоподобия:
в) шаговом регрессионном анализе.
10. Остаточная сумма квадратов равна нулю:
а) когда правильно подобрана регрессионная модель;
б) когда между признаками существует точная функциональная связь;
в) никогда.
11. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
а) 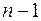 ;
;
б) 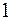 ;
;
в) 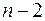 .
.
12. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
а) 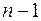 ;
;
б) 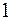 ;
;
в) 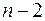 .
.
13. Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
а) 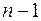 ;
;
б) 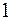 ;
;
в) 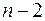 .
.
14. Для оценки значимости коэффициентов регрессии рассчитывают:
а) 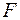 -критерий Фишера;
-критерий Фишера;
б) 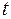 -критерий Стьюдента;
-критерий Стьюдента;
в) коэффициент детерминации 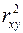 .
.
15. Какое уравнение регрессии нельзя свести к линейному виду:
а) 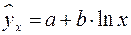 ;
;
б) 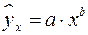 :
:
в)  .
.
16. Какое из уравнений является степенным:
а)  ;
;
б) 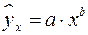 :
:
в)  .
.
17. Параметр 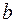 в степенной модели является:
в степенной модели является:
а) коэффициентом детерминации;
б) коэффициентом эластичности;
в) коэффициентом корреляции.
18. Коэффициент корреляции 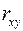 может принимать значения:
может принимать значения:
а) от –1 до 1;
б) от 0 до 1;
в) любые.
19. Для функции 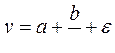 средний коэффициент эластичности имеет вид:
средний коэффициент эластичности имеет вид:
а) 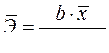 ;
;
б) 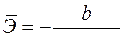 ;
;
в) 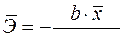 .
.
20. Какое из следующих уравнений нелинейно по оцениваемым параметрам:
а) 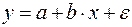 ;
;
б) 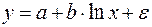 ;
;
в) 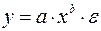 .
.
Дата: 2018-11-18, просмотров: 756.