Часто вместо рассмотрения случайной величины как единого целого можно и удобно разбить ее на постоянную и чисто случайную составляющие, где постоянная составляющая всегда есть ее математическое ожидание. Если 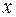 – случайная переменная и  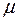– ее математическое ожидание, то декомпозиция случайной величины записывается следующим образом:

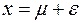,                                                                        (A.14)

где 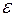 – чисто случайная составляющая.

Конечно, можно было бы посмотреть на это по-другому и сказать, что случайная составляющая 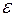 определяется как разность между  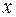и

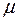
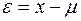.                                                                        (A.15)

Из определения следует, что математическое ожидание величины 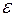 равно нулю:

.

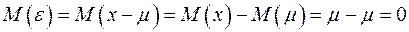Поскольку весь разброс значений 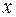 обусловлен 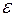, неудивительно, что теоретическая дисперсия  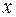равна теоретической дисперсии 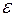. Последнее нетрудно доказать. По определению,

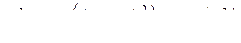
и

    .

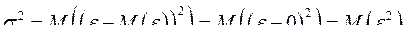Таким образом, 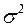 может быть эквивалентно определена как дисперсия  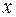или .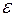

Обобщая, можно утверждать, что если 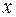 – случайная переменная, определенная по формуле (A.14), где  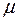– заданное число и  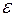– случайный член с  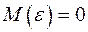и 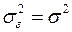, то математическое ожидание величины  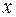равно 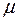, а дисперсия – .

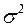Способы оценивания и оценки

До сих пор мы предполагали, что имеется точная информация о рассматриваемой случайной переменной, в частности – об ее распределении вероятностей (в случае дискретной переменной) или о функции плотности распределения (в случае непрерывной переменной). С помощью этой информации можно рассчитать теоретическое математическое ожидание, дисперсию и любые другие характеристики, в которых мы можем быть заинтересованы.

Однако на практике, за исключением искусственно простых случайных величин (таких, как число выпавших очков при бросании игральной кости), мы не знаем точного вероятностного распределения или плотности распределения вероятностей. Это означает, что неизвестны также и теоретическое математическое ожидание, и дисперсия. Мы, тем не менее, можем нуждаться в оценках этих или других теоретических характеристик генеральной совокупности.

Процедура оценивания всегда одинакова. Берется выборка из 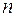 наблюдений, и с помощью подходящей формулы рассчитывается оценка нужной характеристики. Нужно следить за терминами, делая важное различие между способом или формулой оценивания и рассчитанным по ней для данной выборки числом, являющимся значением оценки. Способ оценивания – это общее правило, или формула, в то время как значение оценки – это конкретное число, которое меняется от выборки к выборке.

В табл. A.6 приведены формулы оценивания для двух важнейших характеристик генеральной совокупности. Выборочное среднее 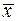 обычно дает оценку для математического ожидания, а формула  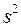– оценку дисперсии генеральной совокупности.

Таблица A.6

Характеристики генеральной совокупности	Формулы оценивания
Среднее,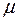
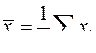
Дисперсия,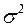

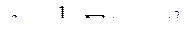
Отметим, что это обычные формулы оценки математического ожидания и дисперсии генеральной совокупности, однако не единственные. Возможно, вы настолько привыкли использовать 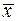 в качестве оценки для 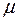, что даже не задумывались об альтернативах. Конечно, не все формулы оценки, которые можно представить, одинаково хороши. Причина, по которой в действительности используется 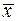, в том, что эта оценка в наилучшей степени соответствует двум очень важным критериям – несмещенности и эффективности. Эти критерии будут рассмотрены ниже.