По первому предельному состоянию найдем распор Н:
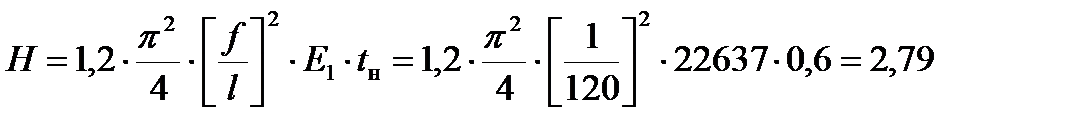 кН/см.
кН/см.
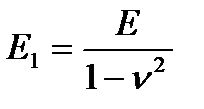 - приведенный модуль жесткости.
- приведенный модуль жесткости.
Таким образом, для нашего случая получим
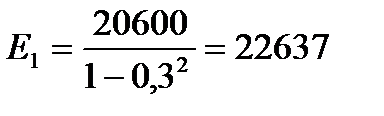 кН/см2,
кН/см2,
Определим катет шва сварного соединения настила и балки настила:
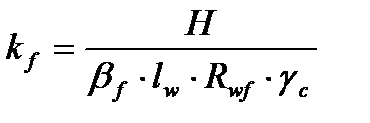 , (4.1)
, (4.1)
где b f – коэффициент проплавления принимаем при полуавтоматической сварке элементов из стали согласно СНиП II -23-81*, равным 0,9;
lw – расчетная длина шва, принимаем равной 1 см;
Rwf – расчетное сопротивление угловых швов срезу по металлу шва согласно СНиП II -23-81* определяется как:
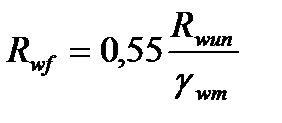 ,
,
где Rwun – нормативное сопротивления металла шва по временному сопротивлению, определяем по СНиП II -23-81* для электрода типа Э42 и марки проволоки Св-08 равно 41 кН/см2;
g wm – коэффициент надежности по материалу по металлу шва, по СНиП II -23-81 равен 1,25.
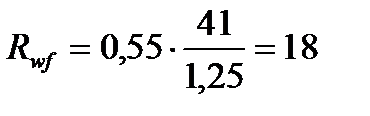 кН/см2.
кН/см2.
Таким образом, с учетом этого расчетная толщина шва сварного соединения настила и балок настила по формуле (4.1) будет
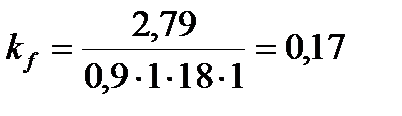 см.
см.
Принимаем kw = 4 мм, так как это минимально допустимый катет.
Расчёт балки настила
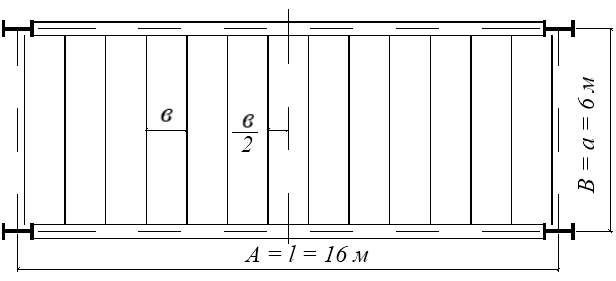
Рис. 4.1. Схема нормального типа балочной клетки
при t =12 мм и b =1200 мм
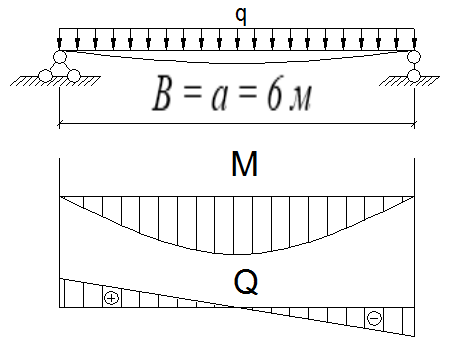
Рис.4.2. Расчётная схема балки настила
Толщина настила tн = 12 мм; шаг балок настила b=1,2м.
Вес 1м2 настила при tн = 12 мм gn= 0,942 кН/м2
Нормативная нагрузка на балку настила
qn = (pn +gn)·b = (22+0,942)·1,2 = 27,53 кН/м
Расчетная нагрузка на балку настила
q= (gp·pn + gg·gn)·b = (1,2·22 + 1,05·0,942)·1,2 =32,87 кН/м
gp= 1,2, gg= 1,05 – коэффициенты надежности
Расчетный изгибающий момент (длина балки настила 6 м)
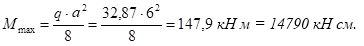
Требуемый момент сопротивления балки настила:
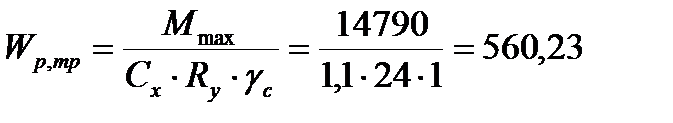 см3.
см3.
При условии Wx>Wтр по ГОСТ 8239-72 принимаем стальной горячекатанный двутавр № 33 с уклоном внутренних граней полок. Для него из сортамента выписываем: Wx = 597 см3; Ix = 9840 см4; g = 42,2 кг/м, ширина полки b=140 мм.
Так как W = 597 см3>Wр,тр= 560,23 см3, то проверяем только прогиб балки настила по формуле:
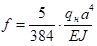 ,
,
здесь l – длина изгибаемой балки, в нашем случае это а=600 см.
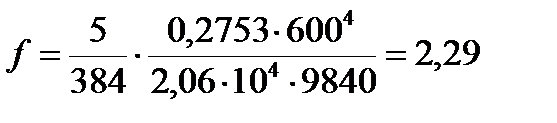 см.
см.
По формуле находим, что наибольший допустимый прогиб для балки такой длины составляет:
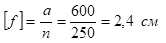
f = 2,29см < 2,4см = [f], следовательно принятая балка удовлетворяет условиям прочности и прогиба. Проверку касательных напряжений в прокатных балках при отсутствии ослабления опорных сечений обычно не производят, так как она легко удовлетворяется из-за относительно большой толщины стенок балок.
Общую устойчивость балок настила проверять не надо, так как их сжатые пояса надежно закреплены в горизонтальном направлении приваренным к ним настилом.
Вычислим общую массу настила и балок настила на одном пролете:
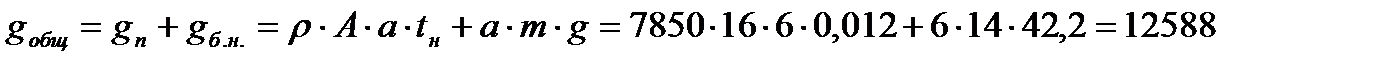 кг,
кг,
тогда расход металла на 1 м2 будет:
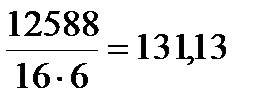 кг/м2.
кг/м2.
4.2. Проектирование и расчет главных балок*
Главные балки – несущие нагрузки от балок настила и настила, являются балками составного сечения. Составные балки используются в тех случаях, когда прокатные балки не удовлетворяют хотя бы одному из условий – прочности, жесткости, общей устойчивости. Проверим необходимость использования составного сечения.
Расчетная схема для главной балки будет выглядеть, как показано на рис. 4.3. Здесь же построены эпюры изгибающих моментов М и поперечных сил Q.
*) Приведённый ниже пример расчёта главной балки выполнен
для балочной клетки с шагом балок настила b= 0,9м, толщине настила tн =0,6см и сечении балки настила – двутавр №22.
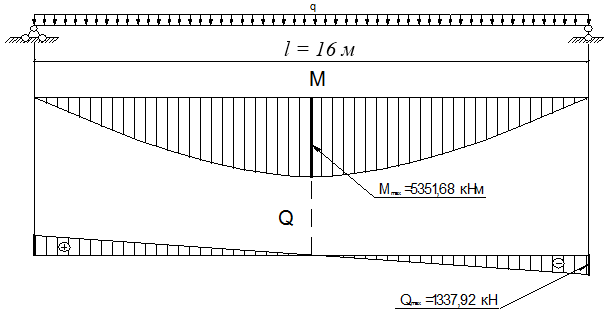
Рис. 4.3 Расчетная схема главной балки
Вес балок настила
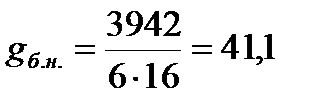 кг/м2 = 0,411 кН/м2.
кг/м2 = 0,411 кН/м2.
Нормативная нагрузка на главную балку
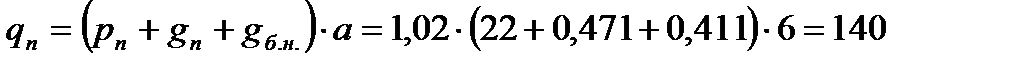 кН/м = 1,4 кН/см.
кН/м = 1,4 кН/см.
Расчетная нагрузка на главную балку с учетом собственного веса главной балки
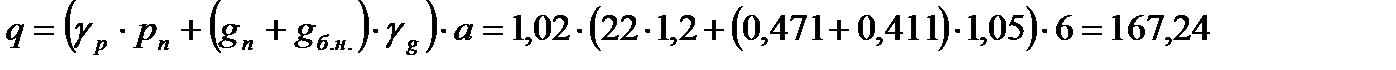 кН/м=
кН/м=
= 1,6724 кН/см
С учетом принятой расчетной схемы и того, что на главную балку действует равномерно распределенная нагрузка, расчетный максимальный изгибающий момент в середине пролета найдем по формуле:
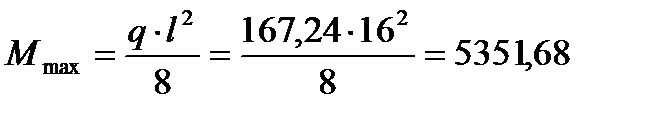 кН×м = 535168 кН×см.
кН×м = 535168 кН×см.
Максимальное значение поперечная сила принимает на опорах и равняется:
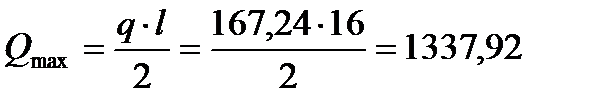 кН.
кН.
Главную балку рассчитываем с учетом развития пластических деформаций. Требуемый момент сопротивления главной балки, первоначально принимая с=1,1:
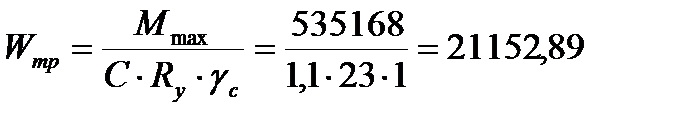 см3.
см3.
Условие Wx>Wтр не выполняется ни для одной прокатной балки даже если не учитывать собственный вес при подсчете нагрузки на балку. Таким образом будем подбирать составное сечение главной балки.
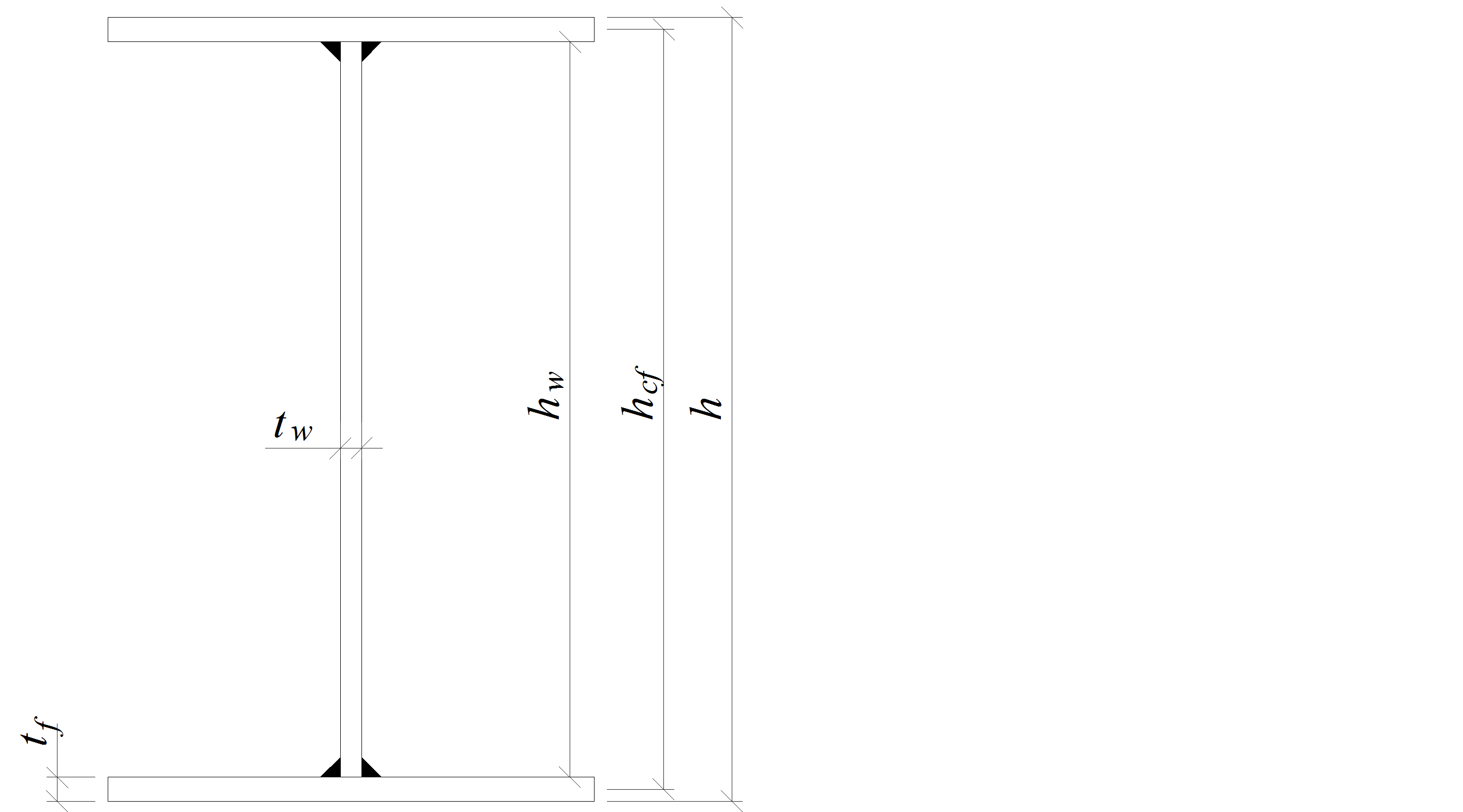 Сечение главной балки будем подбирать двутаврового типа, состоящего из трех листов: вертикального – стенки и двух горизонтальных – полок, которые сваривают в заводских условиях автоматической сваркой.
Сечение главной балки будем подбирать двутаврового типа, состоящего из трех листов: вертикального – стенки и двух горизонтальных – полок, которые сваривают в заводских условиях автоматической сваркой.
Запишем необходимые для расчета величины:
- материал главной балки – сталь С255;
- расчетное сопротивление стали растяжению, сжатию и изгибу Ry = 23 кН/см2 при t³20 мм принимаем по ГОСТ 27772-88;
- расчетное сопротивление стали сдвигу RS принимаем по СНиП II-23-81*:
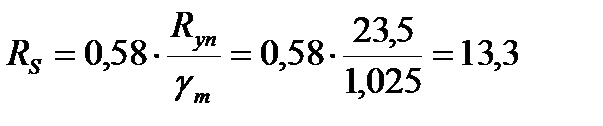 кН/см2.
кН/см2.
- строительная высота перекрытия hстр – не ограничена
- прогиб f < (1/400) l
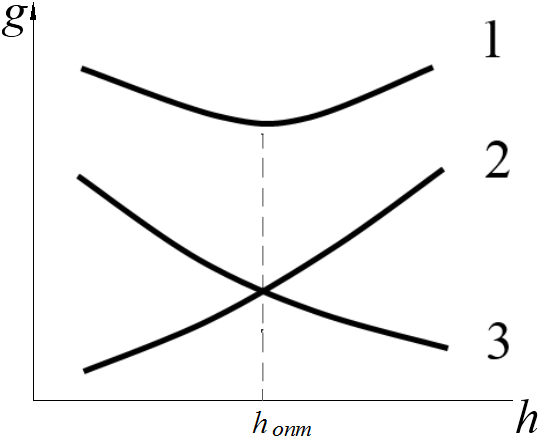 Масса балки состоит из массы ее поясов, стенки и некоторых конструктивных элементов (стыковых накладок, ребер жесткости), учитываемых строительным коэффициентом, причем с увеличением высоты балки масса поясов уменьшается (3), а масса стенки возрастает (2). Так как (как видно из рисунка), функции массы поясов и стенки с изменением высоты балки изменяются неодинаково – одна убывает, а другая возрастает, то существует наименьшее значение суммы обеих функций, т.е. должна быть высота, при которой суммарная масса поясов и стенки будет наименьшей.
Масса балки состоит из массы ее поясов, стенки и некоторых конструктивных элементов (стыковых накладок, ребер жесткости), учитываемых строительным коэффициентом, причем с увеличением высоты балки масса поясов уменьшается (3), а масса стенки возрастает (2). Так как (как видно из рисунка), функции массы поясов и стенки с изменением высоты балки изменяются неодинаково – одна убывает, а другая возрастает, то существует наименьшее значение суммы обеих функций, т.е. должна быть высота, при которой суммарная масса поясов и стенки будет наименьшей.
Определим оптимальную высоту 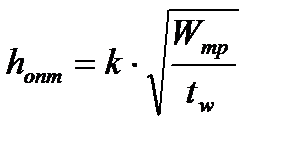 балки, предварительно задав ее высоту:
балки, предварительно задав ее высоту:
h » (1/10) l »1,6 м
и рассчитав толщину стенки
tw = 7+3·1600/1000 = 11,8 мм = 12 мм
По справочным данным определим, что k = 1,15.
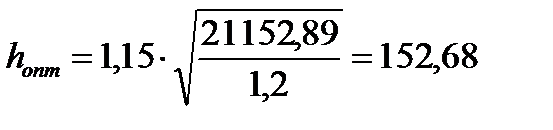 см = 150 см.
см = 150 см.
Из условия жесткости главной балки найдем величину минимальной высоты главной балкиhmin:
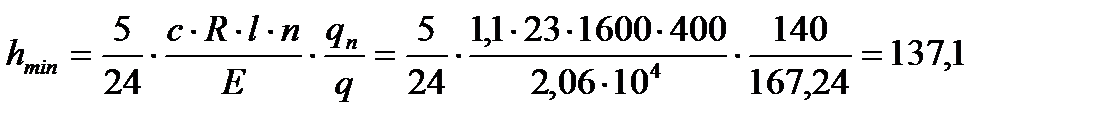 см.
см.
В целях унификации конструкции примем окончательное значение высоты балки кратное 100 мм, т.е. h =140 см.
Проверяем принятую толщину стенки:
по эмпирической формуле
tw = 7+3·1400/1000 = 11,2 мм
из условия работы стенки на касательные напряжения на опоре
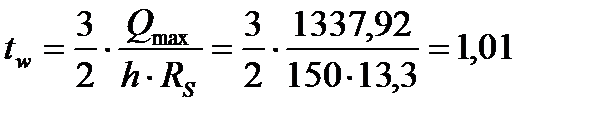 см<1,2 см
см<1,2 см
Чтобы не применять продольных ребер жесткости
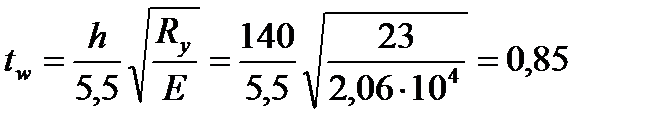 см<1,2 см.
см<1,2 см.
Сравнивая полученную расчетным путем толщину стенки с принятой (12 мм), приходим к выводу, что она удовлетворяет условию прочности на действие касательных напряжений и не требует укрепления ее продольным ребром жесткости для обеспечения местной устойчивости.
Найдем размеры горизонтальных листов пояса исходя из необходимой несущей способности балки. Для этого вычислим требуемый момент инерции сечения балки:
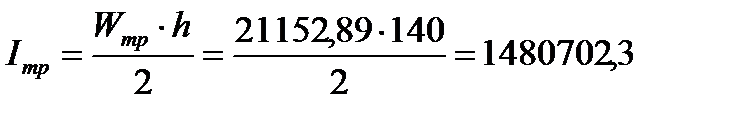 см4,
см4,
который распределяется на момент инерции стенки и двух поясов балки:
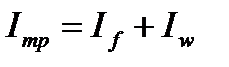 .
.
Принимаем толщину поясов балки tf = 20 мм, тогда высота стенки балки будет равной
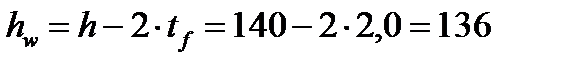 см,
см,
Момент инерции стенки балки
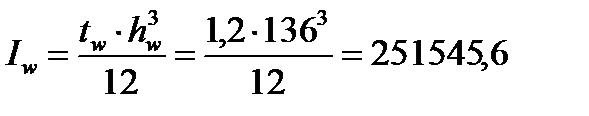 см4.
см4.
Момент инерции, приходящийся на поясные листы
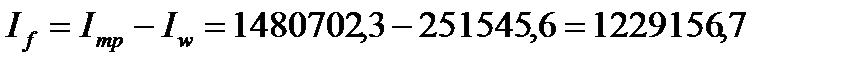 см4.
см4.
Момент инерции поясных листов балки относительно ее нейтральной оси, пренебрегая моментом инерции поясов относительно их собственной оси ввиду его малости, будет равен
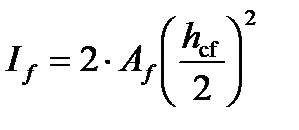 ,
,
где h- расстояние между параллельными осями поясов балки
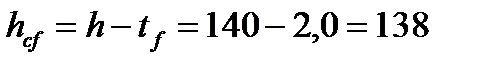 см.
см.
Отсюда получаем требуемую площадь сечения одного пояса балки
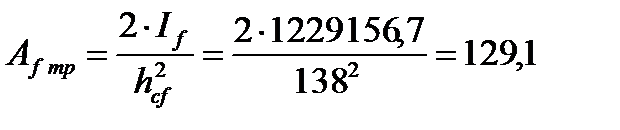 см2.
см2.
Находим требуемое значение ширины пояса балки:
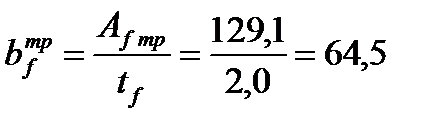 см.
см.
Окончательно примем bf = 650 мм.
Принимаем пояса из универсальной стали 650х20 мм, для которой 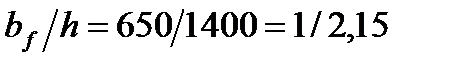 , что находится в пределах рекомендуемого отношения.
, что находится в пределах рекомендуемого отношения.
Уточняем принятый ранее коэффициент учета пластической работы с исходя из:
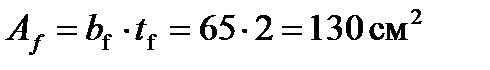 ;
;
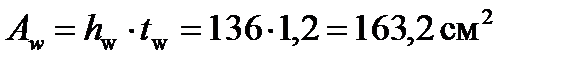 ;
;
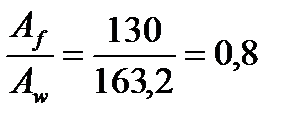
Принимаем с=1,08, которое практически соответствует заданному с=1,1
Проверим отношение ширины свеса сжатого пояса к его толщине из соображений местной устойчивости (СНиП II-23-81* ):
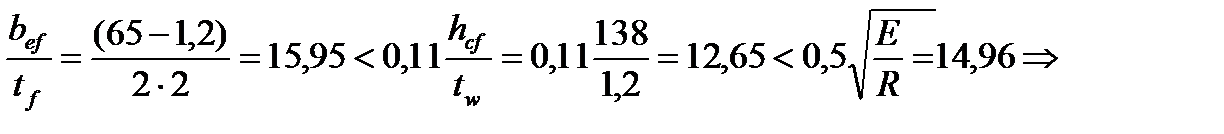 принятое соотношение размеров пояса не удовлетворяет условию его местной устойчивости. Увеличим толщину поясов балки до tf = 24 мм и произведем новый расчет.
принятое соотношение размеров пояса не удовлетворяет условию его местной устойчивости. Увеличим толщину поясов балки до tf = 24 мм и произведем новый расчет.
Принимаем толщину поясов балки tf = 24 мм, тогда высота стенки балки будет равной
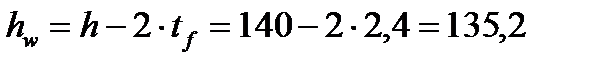 см,
см,
Момент инерции стенки балки
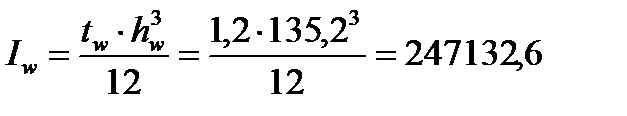 см4.
см4.
Момент инерции, приходящийся на поясные листы
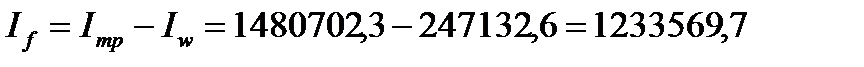 см4.
см4.
Момент инерции поясных листов балки относительно ее нейтральной оси, пренебрегая моментом инерции поясов относительно их собственной оси ввиду его малости, будет равен
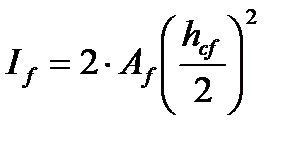 ,
,
где h- расстояние между параллельными осями поясов балки
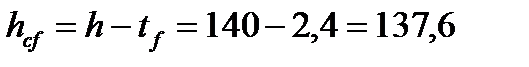 см.
см.
Отсюда получаем требуемую площадь сечения поясов балки
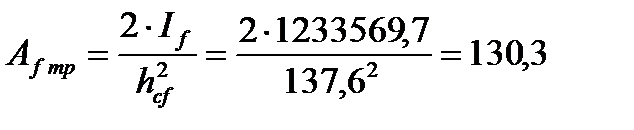 см2.
см2.
Находим требуемое значение ширины пояса балки:
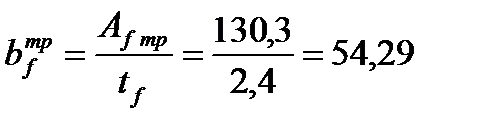 см.
см.
Окончательно примем bf= 550 мм.
Принимаем пояса из универсальной стали 550х24 мм, для которой 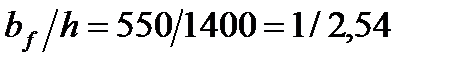 , что находится в пределах рекомендуемого отношения.
, что находится в пределах рекомендуемого отношения.
Уточняем принятый ранее коэффициент учета пластической работы с исходя из:
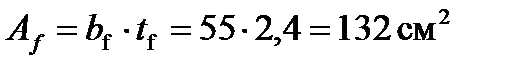 ;
;
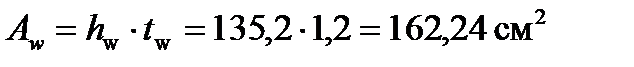 ;
;
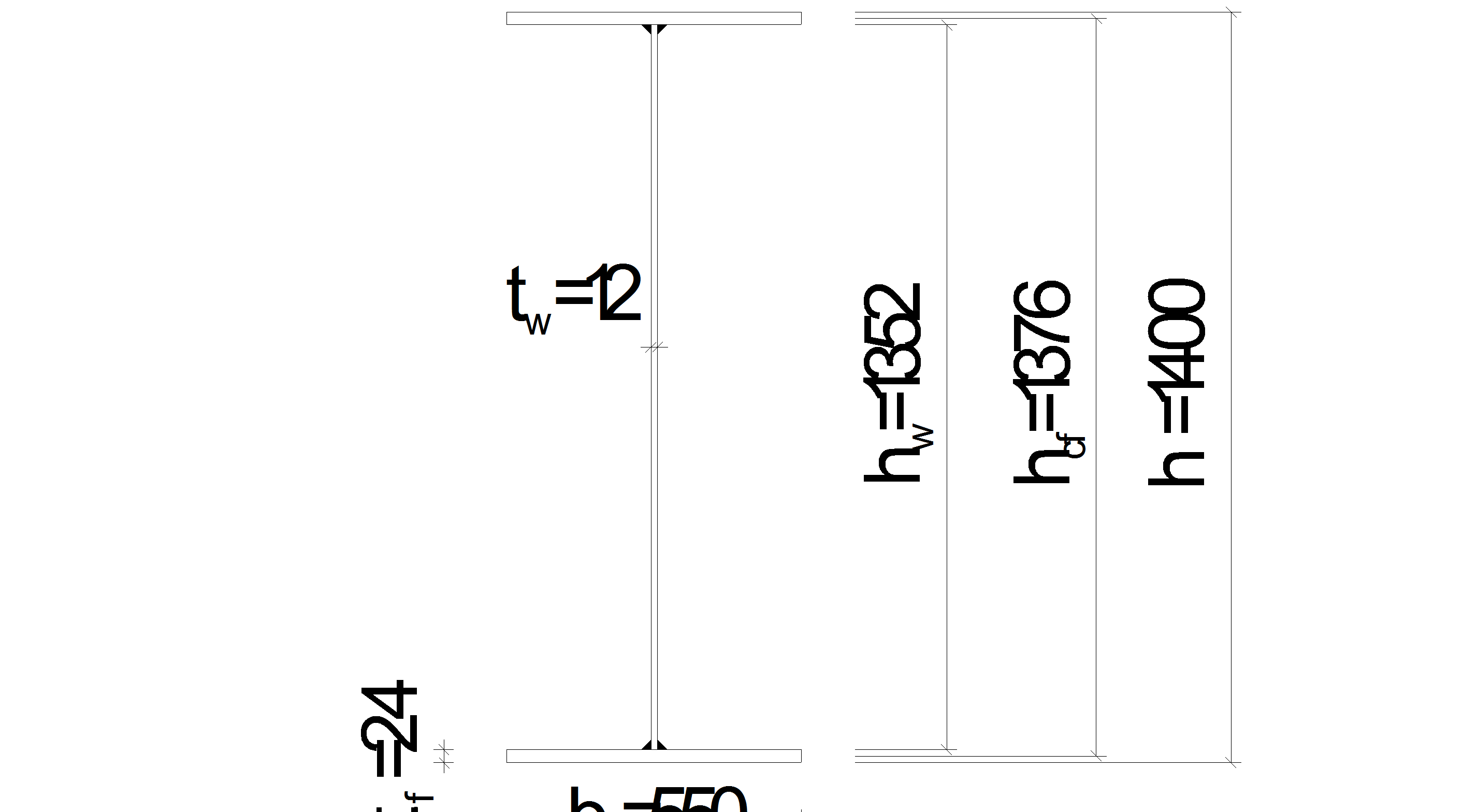
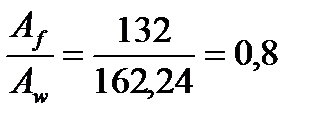
Принимаем с=1,09, которое практически соответствует заданному с=1,1
Проверим отношение ширины свеса сжатого пояса к его толщине из соображений местной устойчивости (по п.7.24 СНиП II-23-81*):
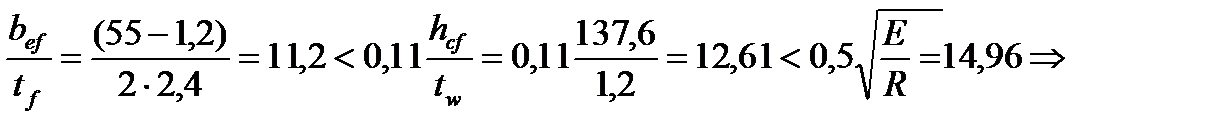 принятое соотношение размеров пояса удовлетворяет условию его местной устойчивости.
принятое соотношение размеров пояса удовлетворяет условию его местной устойчивости.
Проверяем несущую способность балки исходя из устойчивости стенки в области пластических деформаций балки в месте действия максимального момента, где Q=0 и τ=0.
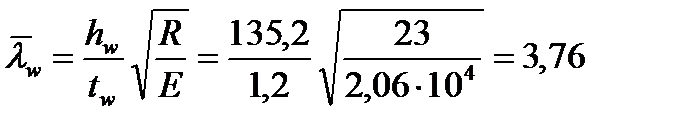 ;
;
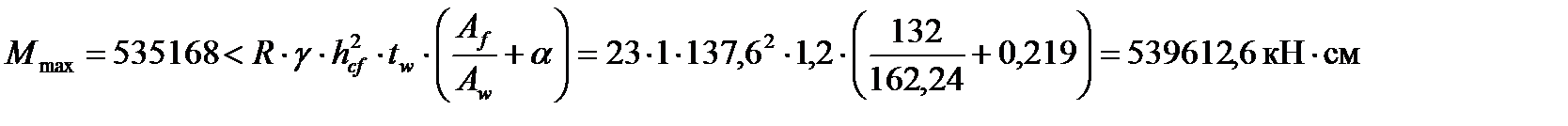
где 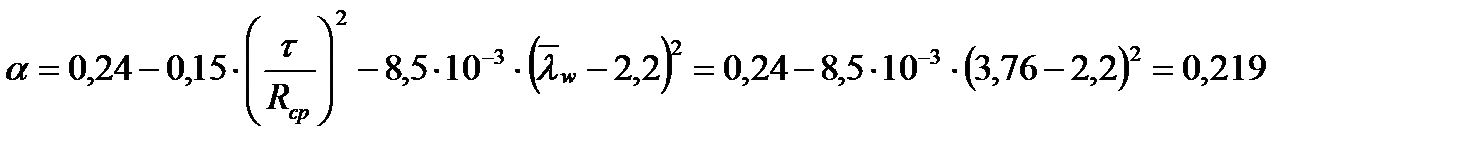
Подобранное сечение балки проверяем на прочность. Определим момент инерции балки:
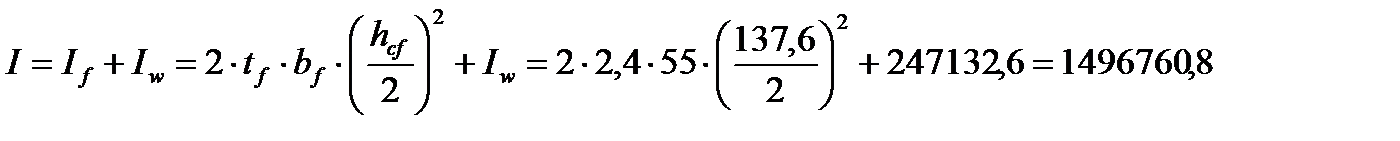 см4.
см4.
Определим момент сопротивления балки:
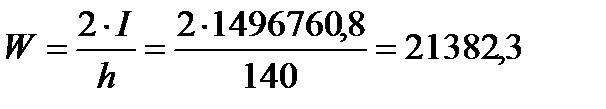 см3.
см3.
Проверим нормальные напряжения в балке по следующей формуле:
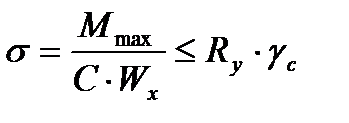 ,
,
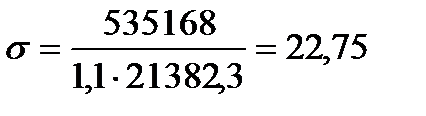 кН/см2< 23×1 = 23 кН/см2,
кН/см2< 23×1 = 23 кН/см2,
следовательно, подобранное сечение удовлетворяет условию прочности.
Проверку прогиба делать нет необходимости, так как принятая высота сечения главной балки больше минимальной и регламентированный прогиб будет обеспечен.
4.2.1.Изменение сечения главной балки по длине
Сечение составной балки, подобранное по максимальному изгибающему моменту, можно уменьшить в местах снижения моментов (у опор). Однако каждое изменение сечения, дающее экономию металла, несколько увеличивает трудоемкость изготовления балки, и поэтому оно экономически целесообразно для балок пролетом более 12 м, что справедливо для нашего случая (16 м).
При равномерной нагрузке наивыгоднейшее по расходу стали место изменения сечения поясов однопролетной сварной балки находится на расстоянии примерно l/6 пролета балки от опоры: 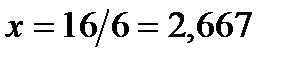 м /1/.
м /1/.
Определим момент и поперечную силу в месте изменения сечения 1-1:
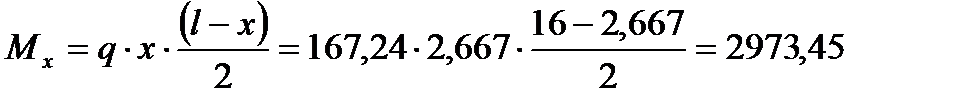 кН×м = 297345 кН×см;
кН×м = 297345 кН×см;
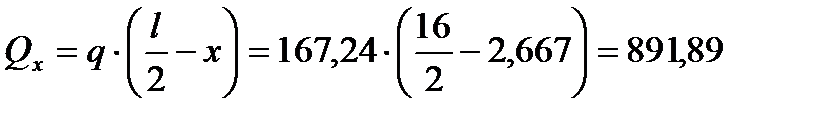 кН.
кН.
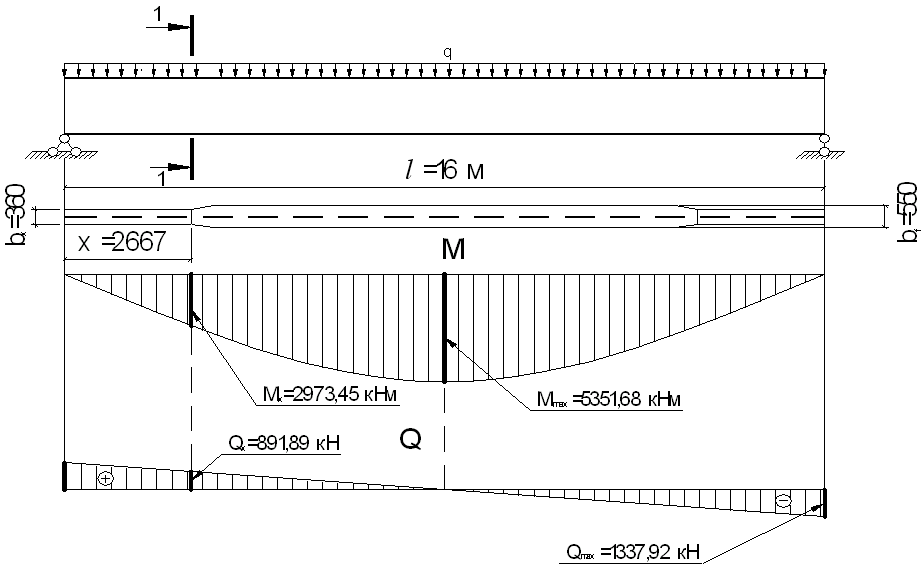
Рис. 4.4 Расчетная схема к уменьшению сечения балки.
Производимый подбор измененного сечения ведем в упругой стадии работы материала. Определим требуемый момент сопротивления и момент инерции измененного сечения, исходя из прочности сварного стыкового шва, работающего на растяжение:
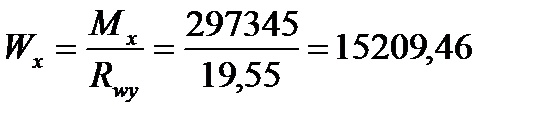 см3,
см3,
где Rwy= 0,85·Ry = 0,85·23 = 19,55 кН/см2.
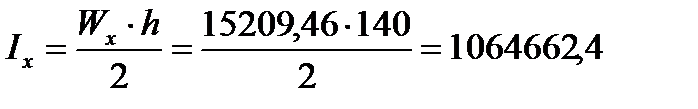 см4.
см4.
Определим требуемый момент поясов, учитывая то, что момент инерции стенки остался тем же:
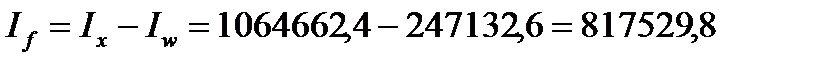 см4.
см4.
Требуемая площадь сечения одного уменьшенного пояса балки:
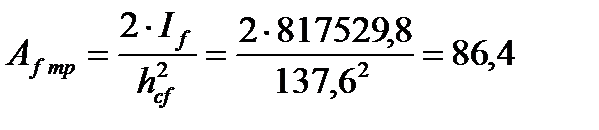 см2.
см2.
Находим требуемое значение ширины пояса:
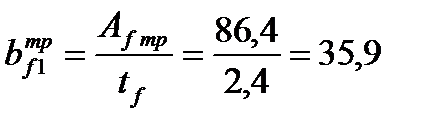 см.
см.
Окончательно примем bf 1 = 360 мм.
Принимаем пояса из универсальной стали 360х24 мм
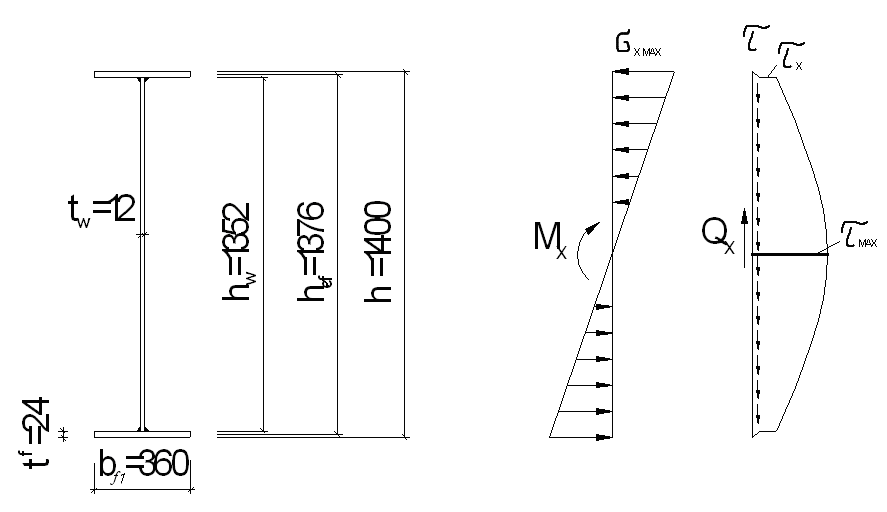
Рис. 4.5. Схема уменьшенного сечения главной балки
Принятый пояс удовлетворяет условиям:
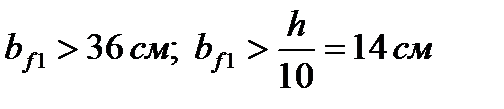 .
.
Проверим на прочность подобранное сечение балки. Определим момент инерции балки:
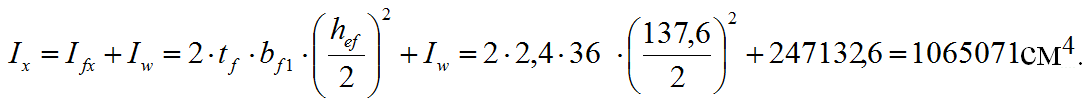 Определим момент сопротивления балки:
Определим момент сопротивления балки:
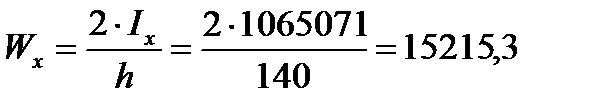 см3.
см3.
Тогда
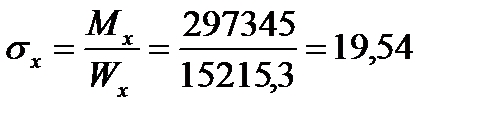 кН/см2 < 23×1 = 23 кН/см2,
кН/см2 < 23×1 = 23 кН/см2,
Следовательно, выбранная балка проходит по нормальному напряжению в месте изменения сечения.
4.2.2. Проверка прочности и общей устойчивости главной балки
Проведем проверку прочности балки.
Проверка максимального нормального напряжения в середине балки и в месте изменения сечения была выполнена выше.
Проверим максимальное касательное напряжение в стенке на нейтральной оси сечения около опоры балки:
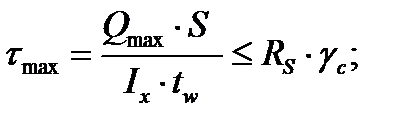
где S-статический момент полусечения балки
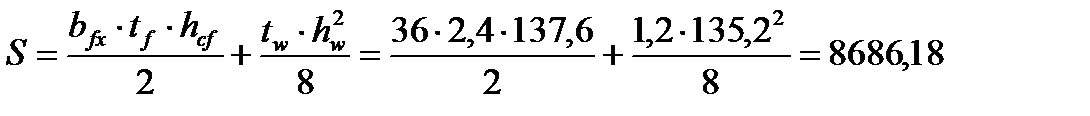 см3.
см3.
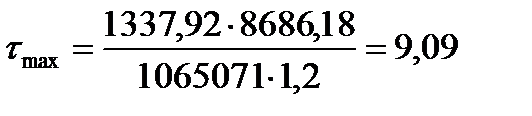 кН/см2 < 13,3×1 = RS×gc.
кН/см2 < 13,3×1 = RS×gc.
Проверим местные напряжения в стенке под балками настила:
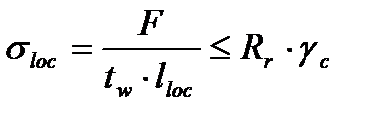 ,
,
где F – расчетные значения опорных реакций балок настила:
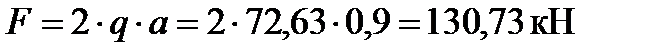 ,
,
где q=72,63 кН/м – расчетная нагрузка на балку настила c учетом собственного веса балки;
а = 0,9 – шаг балок настила,
lloc– длина передачи нагрузки на стенку главной балки:
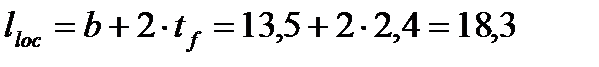 см.
см.
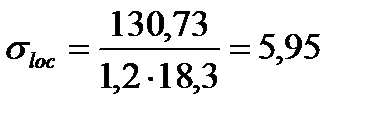 кН/см2 < Ry×gc = 23 кН/см2.
кН/см2 < Ry×gc = 23 кН/см2.
Наличие местных напряжений, действующих на стенку балки, требует проверки совместного действия нормальных, касательных и местных напряжений на уровне поясного шва и под балкой настила по уменьшенному сечению вблизи места изменения сечения пояса. В рассматриваемом примере такого места нет, так как под ближайшей балкой настила будет стоять ребро жесткости, которое воспринимает давление балок настила, и передачи локального давления на стенку в этом месте не будет. Поэтому проверяем приведенные напряжения в месте изменения сечения 1-1 балки (где они будут максимальны) по формуле:
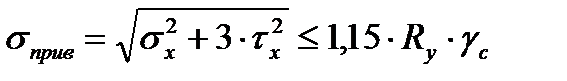 ,
,
где
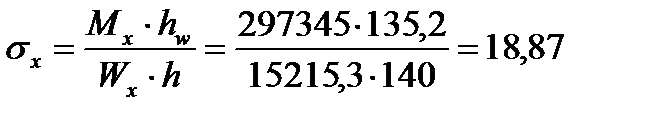 кН/см2,
кН/см2,
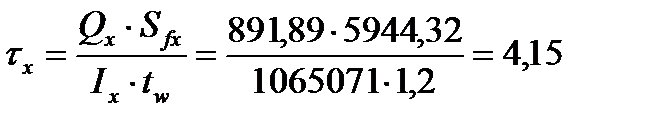 кН/см2
кН/см2
где
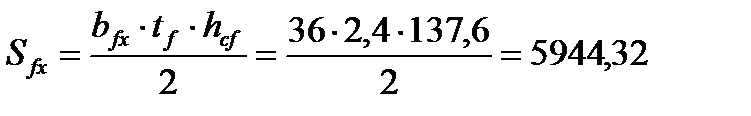 см3,
см3,
тогда, получим
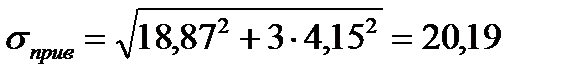 кН/см2
кН/см2 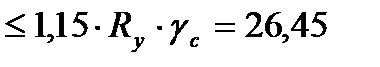 кН/см2.
кН/см2.
Из этих проверок следует, что прочность балки обеспечена.
Проверяем общую устойчивость балки.
Проверим общую устойчивость в месте действия максимальных нормальных напряжений, принимая за расчетный пролет lef = 90 см - расстояние между балками настила. Условие устойчивости записывается в виде:
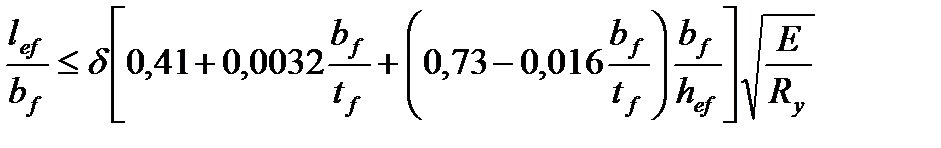
где lef – расчетная длина балки между связями, препятствующими поперечным смещениям сжатого пояса балки;
bf – ширина сжатого пояса (ширина полки);
tf – толщина сжатого пояса (толщина полки);
hef – расстояние (высота) между осями поясных листов.
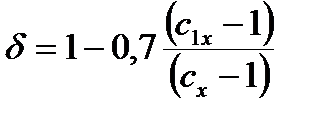
Условия применения уравнения устойчивости плоской формы изгиба:
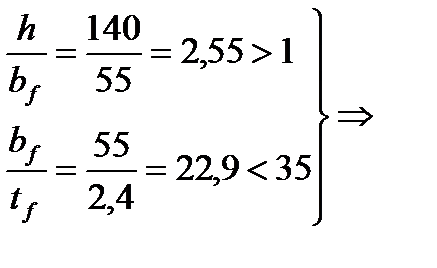 применение формулы возможно.
применение формулы возможно.
При t=0 и с1х=сх получаем 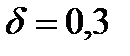
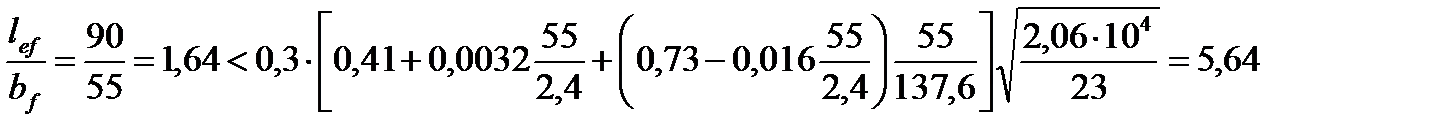 .
.
Проверим общую устойчивость в месте уменьшенного сечения главной балки (балка работает упруго и 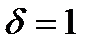 ):
):
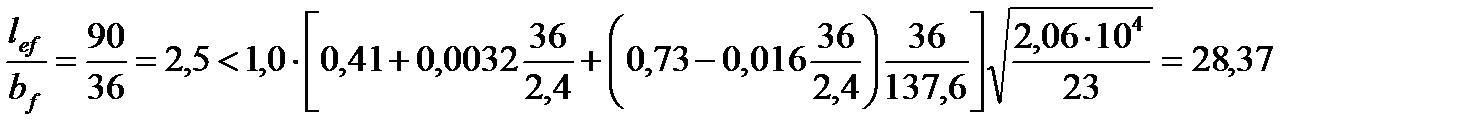 .
.
Обе проверки показали, что общая устойчивость балки обеспечена.
Проверка прогиба.
Проверку главной балки по второму предельному состоянию (проверку прогиба) производить нет надобности, так как принятая высота балки h =140 см > 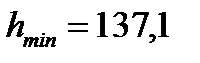 см.
см.
Проверка местной устойчивости сжатого пояса и стенки сварной балки
Проверка устойчивости сжатого пояса.
Эту проверка производится в месте возникновения максимальных нормальных напряжений – в середине пролета главной балки.
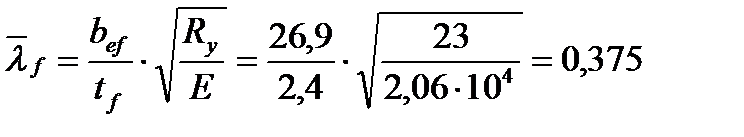
где bef – расстояние от грани стенки до края поясного листа – полки:
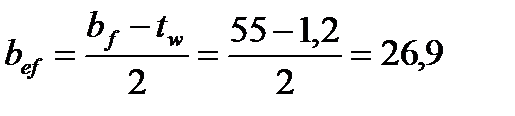 - свес пояса
- свес пояса
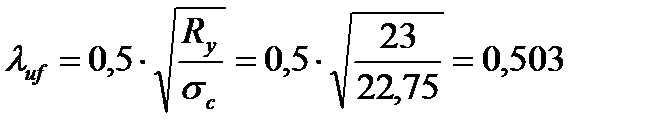
Поскольку 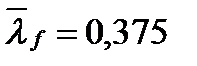 <
< 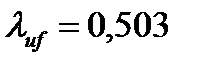 , то можно считать, что местная устойчивость сжатой полки балки обеспечена.
, то можно считать, что местная устойчивость сжатой полки балки обеспечена.
4.2.3. Проверка устойчивости стенки
Определим необходимость укрепления стенки поперечными ребрами жесткости по п. 7.10 СНиПа II-23-81*. Стенки балок следует укреплять поперечными ребрами жесткости, если значение условной гибкости стенки балки`lw превышает 2,2.
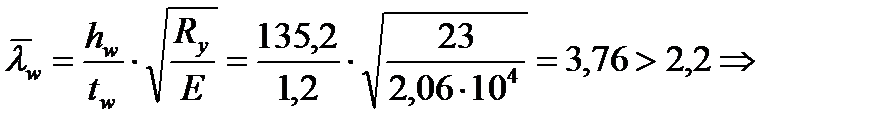 поперечные ребра жесткости необходимы. Кроме того, в зоне учета пластических деформаций необходима постановка ребер жесткости под каждой балкой настила, так как местные напряжения в стенке в этой зоне недопустимы.
поперечные ребра жесткости необходимы. Кроме того, в зоне учета пластических деформаций необходима постановка ребер жесткости под каждой балкой настила, так как местные напряжения в стенке в этой зоне недопустимы.
Расстановку вертикальных ребер жесткости принимаем согласно рис. 4.6 через промежуток а = 270 см. Это расстояние удовлетворяет условию СНиПа II-23-81*, которое между основными поперечными ребрами не должно превышать 2·hw, т.к. 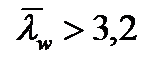
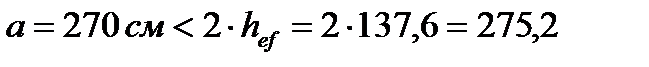 см
см
Должно быть также соблюдено конструктивное требование: каждая вторая, или третья балка настила должна опираться на ребро.
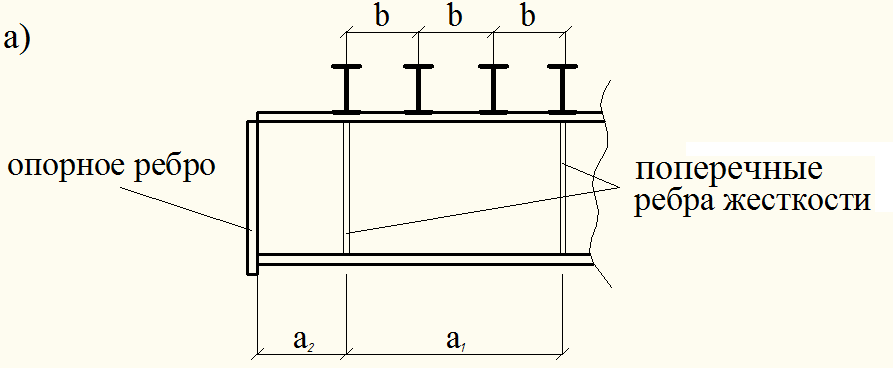

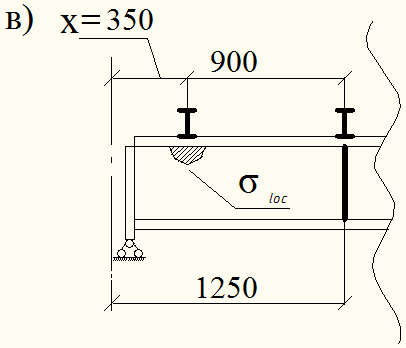
Рис. 4.6. Пояснение к способу расстановки поперечных рёбер жёсткости: а) фрагмент опорной части главной балки; б) схема расстановки поперечных рёбер жёсткости; в) к расчёту локальных (местных) напряжений от балки настила.
Согласно СНиП II-23-81*, так как`lw = 3,76 > 2,5, то проверка устойчивости стенок обязательна.
Проверим местную устойчивость стенки в сечении 2-2, для этого определяем средние значения M2 и Q2 на расстоянии х2 = 395 см от опоры (под балкой настила), что почти совпадает с рекомендацией расстояния в 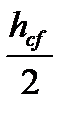 от края отсека.
от края отсека.
В этом сечении возникают следующие усилия:
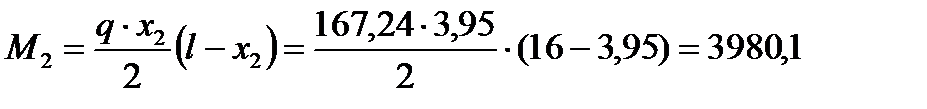 кНм,
кНм,
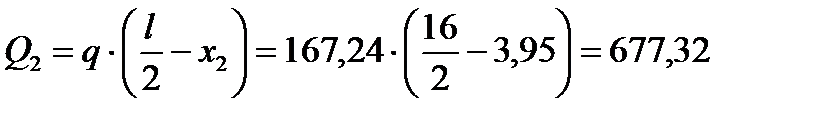 кН.
кН.
И соответствующие этим усилиям напряжения будут равны:
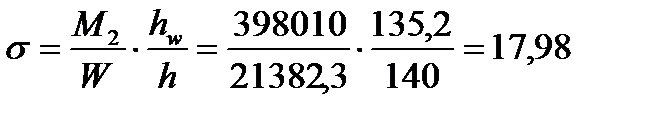 кН/см2,
кН/см2,
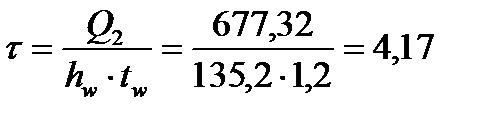 кН/см2.
кН/см2.
Проверим местные напряжения в стенке под балками настила:
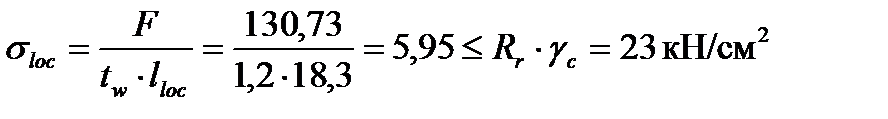 ,
,
Определяем критические напряжения:
,
Где 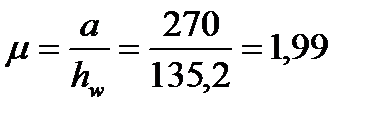 ,
, 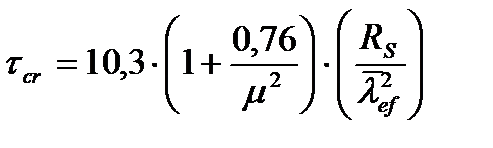
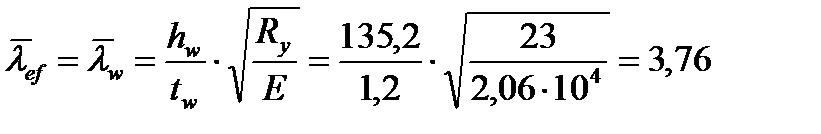
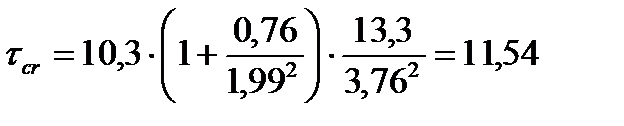 кН/см2.
кН/см2.
Размеры отсека  и
и 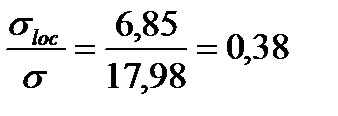
Предельное значение этого отношения находим по табл. 24 СНиПа II-23-81*, в зависимости от значения коэффициента d, учитывающего степень упругого защемления стенки в поясах:
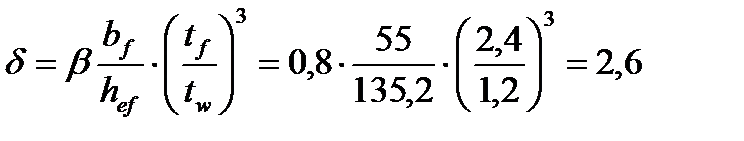 ,
,
где b = 0,8, коэффициент принимаемый по табл. 22 СНиПа II-23-81*;
Тогда 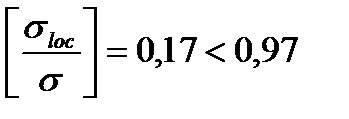 .
.
Расчет на местную устойчивость стенки будем проводить по п. 7.6. в (СНиПа II-23-81*).
Критические нормальные напряжения:
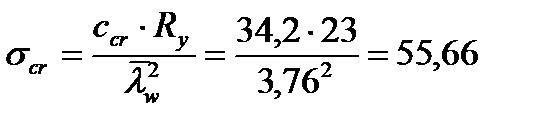 кН/см2;
кН/см2;
Определяем 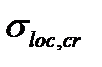 , подставляя вместо а значение а/2:
, подставляя вместо а значение а/2:
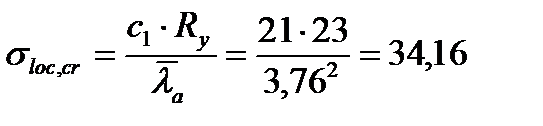 кН/см2,
кН/см2,
где 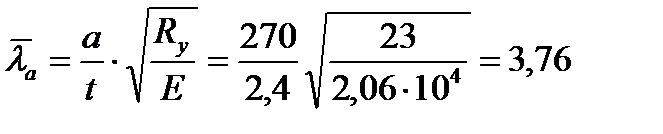 .
.
С учетом этого, по формуле (79) СНиПа II-23-81* получим:
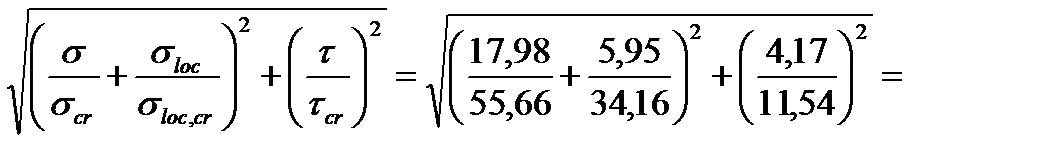
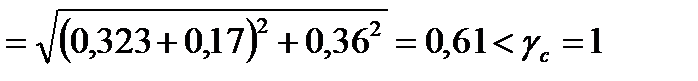 .
.
Проверка показала, что устойчивость стенки обеспечена и постановка ребер жесткости на расстоянии 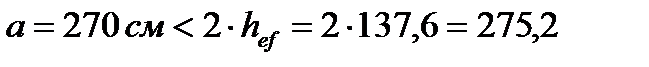 см возможна.
см возможна.
Помимо проверки устойчивости стенки в области больших нормальных напряжений необходимо также проверить ее устойчивость и в области больших касательных напряжений - вблизи от опоры балки. Проверим на устойчивость стенки в сечении 3-3, для этого определяем средние значения M3 и Q3 на расстоянии х3 = 125 см от опоры (под балкой настила), что почти совпадает с рекомендацией расстояния 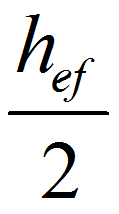 от края отсека.
от края отсека.
В этом сечении возникают следующие усилия:
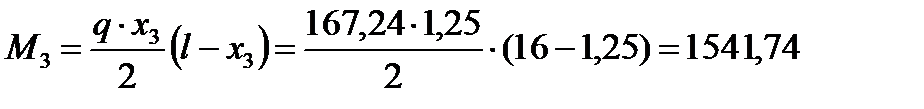 кНм,
кНм,
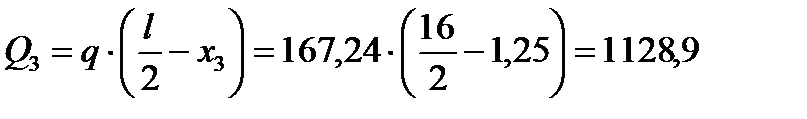 кН.
кН.
И соответствующие этим усилиям напряжения будут равны:
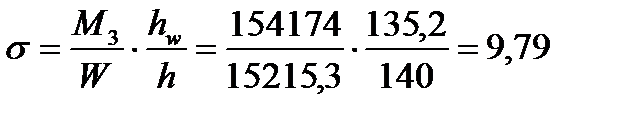 кН/см2,
кН/см2,
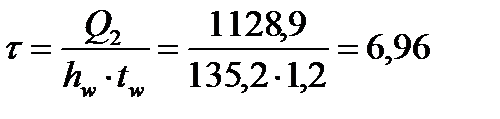 кН/см2.
кН/см2.
Проверим местные напряжения в стенке под балками настила:
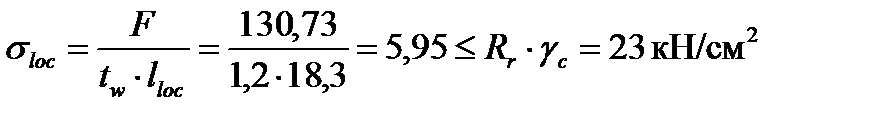 ,
,
Определяем критические напряжения:
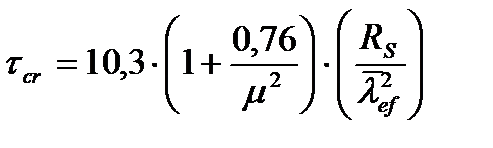 ,
,
Где 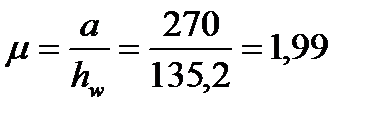 ,
, 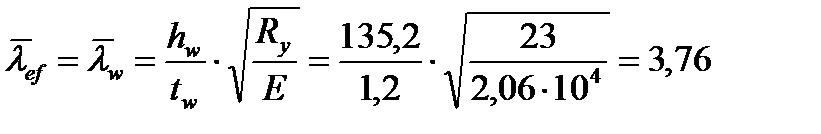
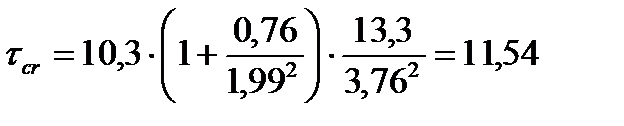 кН/см2.
кН/см2.
Размеры отсека 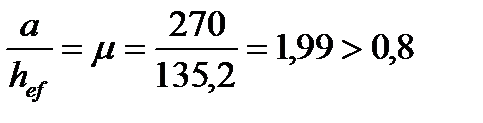 и
и 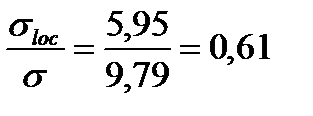
Предельное значение этого отношения находим по табл. 24 СНиПа II-23-81.
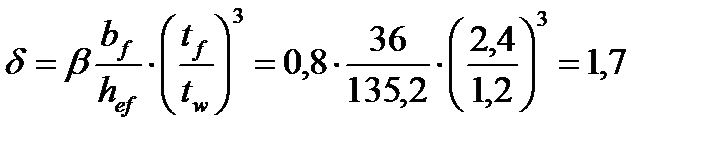 ,
,
Тогда 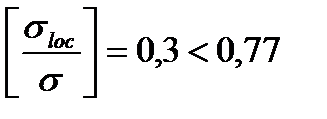 .
.
Расчет на местную устойчивость стенки будем проводить по п. 7.6, в СНиПа II-23-81*.
Критические нормальные напряжения:
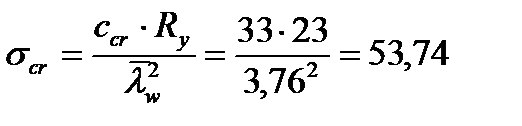 кН/см2;
кН/см2;
Определяем 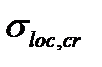 , подставляя вместо а значение а/2:
, подставляя вместо а значение а/2:
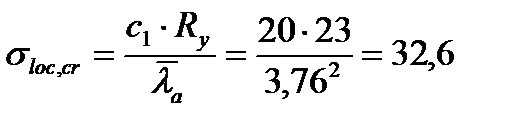 кН/см2,
кН/см2,
где 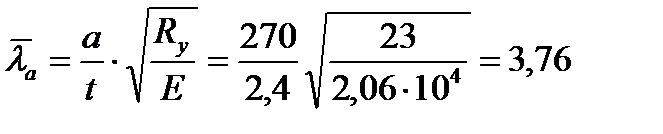 .
.
С учетом этого, по формуле (79) СНиПа II-23-81* получим:
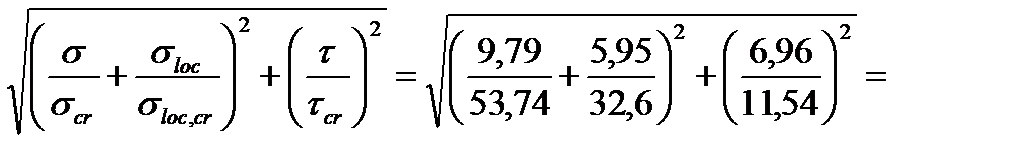
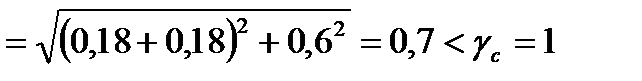 .
.
Обе проверки показали, что запроектированная балка удовлетворяет требованиям прочности, прогиба, общей и местной устойчивости.
4.2.4. Расчет поясных швов главной балки
Так как балка работает с учетом пластических деформаций, то швы выполняем двусторонние, автоматической сваркой в лодочку, сварной проволокой Св-08А.
Катет шва определим под первой от опоры балкой настила, где сдвигающая сила максимальна, то есть в сечении х = 25 см.
Катет сварного шва определяется по формуле:
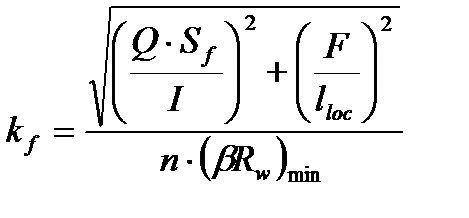 ,
,
где n = 1 при односторонних швах, n = 2 при двусторонних швах;
(bRw)min – произведение глубины проплавления на расчетное сопротивление для расчетного сечения.
Из пункта 3.2.1 возьмем уже рассчитанные величины:
Iх = 1065071 см4; Sf х = 5944,32 cм3; F = 150,52 кН; lloc = 18,3 см.
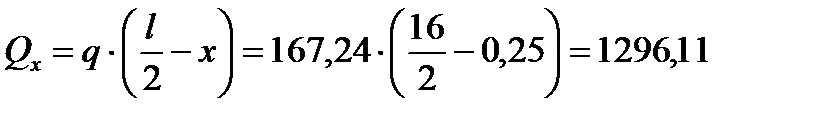 кН;
кН;
По табл. 4 СНиП II-23-81* определим значение нормативного сопротивления металла шва по временному сопротивлению Rwun = 41 кН/см2. Тогда расчетное сопротивление углового шва условному срезу по металлу шва:
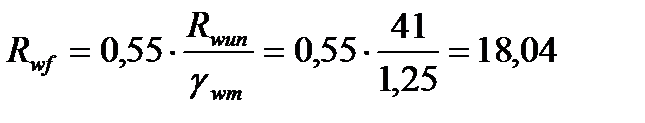 кН/см2,
кН/см2,
где gwm = 1,25, - коэффициент надежности по материалу шва.
По табл. 51 СНиП II-23-81* для стали С255 определим временное сопротивление стали разрыву Run = 37 кН/см2. Тогда расчетное сопротивление углового шва условному срезу по металлу границы сплавления:
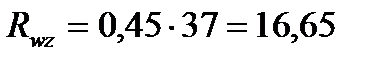 кН/см2.
кН/см2.
По табл. 34 СНиП II-23-81* для выбранного типа сварки примем соответствующие коэффициенты для расчета углового шва:
bf = 1,1 – по металлу шва;
bz = 1,15 – по металлу границы сплавления.
Определим, какое сечение в соединении является расчетным (более опасное):
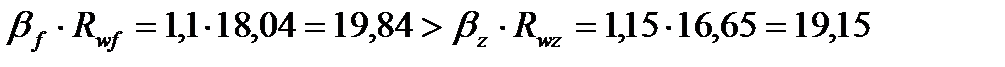 кН/см2, Þ расчетным является сечение по металлу границы сплавления.
кН/см2, Þ расчетным является сечение по металлу границы сплавления.
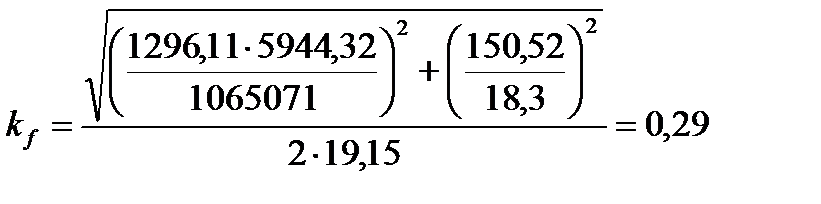 см.
см.
По табл. 38 СНиП II-23-81* для пояса толщиной 24 мм принимаем катет шва, равный минимальному kf = 7 мм, что больше, получившегося по расчету – 2,9 мм.
4.2.5. Расчет опорного ребра главной балки
Размеры опорных ребер определим из расчета на смятие торца ребра: 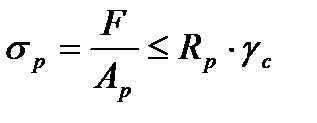 ,
,
где F - опорная реакция балки N (будет равна значению поперечной силы на торце балки, найденной выше):
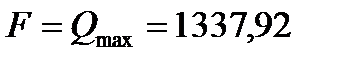 кН;
кН;
Rp – расчетное сопротивление смятию торцевой поверхности, по табл. 1 СНиПа II-23-81* находим:
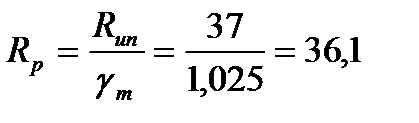 кН/см2,
кН/см2,
где по табл. 51 СНиП II-23-81* для стали С255 определим временное сопротивление стали разрыву Run = 37 кН/см2; по табл. 2* СНиП II-23-81* для стали по ГОСТу 27772-88, находим, что коэффициент надежности по материалу gm = 1,025.
Найдем требуемую площадь опорного ребра:
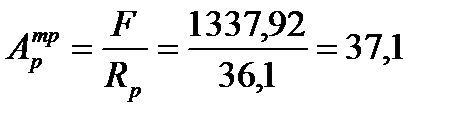 см2.
см2.
Уже принятая ширина пояса bf1 = 36 cм, следовательно толщину ребра определим, как
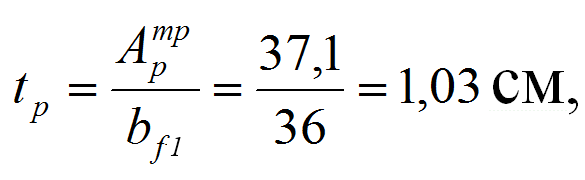
принимая окончательно tp = 12 мм.
Тогда
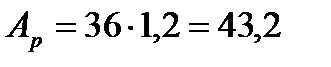 см2
см2 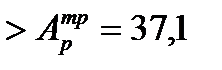 см2,
см2,
сечение подобранного торца балки проходит проверку на смятие.
Проверим опорный участок балки на устойчивость из плоскости балки, как условного опорного стержня, включающего в площадь своего сечения опорное ребро и часть стенки балки длиной bw (рис. 4.7).
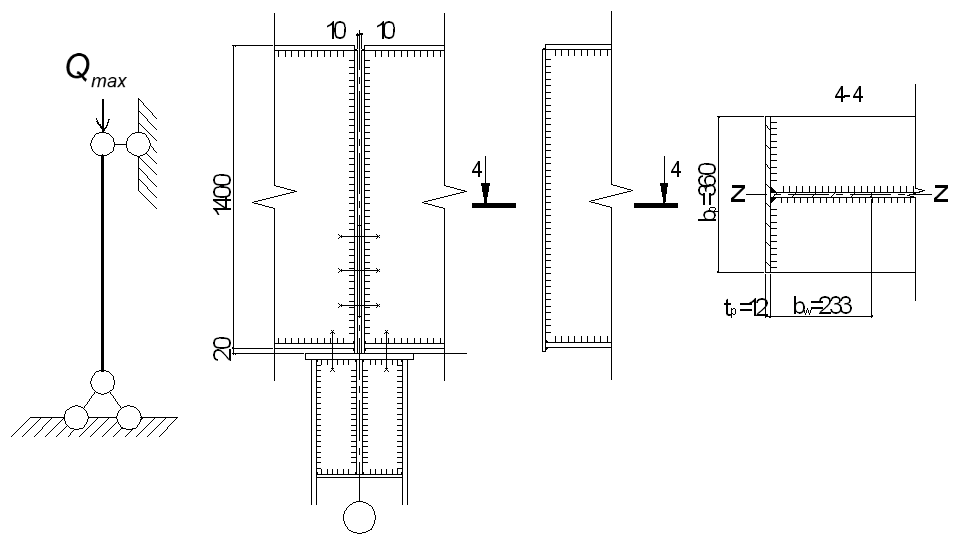
Дата: 2018-12-21, просмотров: 1176.