РАЗДЕЛ I . ВВЕДЕНИЕ В ЭКОНОМИЧЕСКУЮ ТЕОРИЮ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

РАЗДЕЛ I . ВВЕДЕНИЕ В ЭКОНОМИЧЕСКУЮ ТЕОРИЮ

Тема Экономика как наука. Экономические системы

Тестовые задания

Наиболее полным и корректным определением предмета науки экономики является следующее

а) экономика изучает переменные величины, поведение которых воздействует на состояние народного хозяйства (цены, производство, занятость и т.д.);

б) экономика изучает деятельность, включающую производство и обмен товарами;

в) экономика изучает, деньги, банковскую систему, капитал;

г) экономика изучает, как общество использует ограниченные ресурсы, необходимые для производства различных товаров в целях удовлетворения своих безграничных потребностей.

Позитивная экономическая теория изучает

а) то, что есть в экономической жизни общества, т.е. функциональные зависимости в экономике;

б) оценочные сведения;

в) модели экономического развития страны;

г) то, что должно быть в экономике, т.е. сущностные взаимосвязи.

Раздел экономики, изучающий поведение хозяйствующих субъектов называется

а) экономическая политика;

б) макроэкономика;

в) микроэкономика;

г) мезоэкономика.

4. Процесс определения доли, соответственно которой каждый хозяйствующий субъект принимает участие в произведенном продукте, называется

а) распределением;

б) производством;

в) обменом;

г) потреблением.

Установите соответствие между отдельными приемами и методами исследования экономики

а) формулировка экономического вывода на основе отдельных фактов;

б) формулировка экономического вывода на основе общих положений;

в) экономические явления исследуются так, как они существуют на самом деле;

г) перенос одного или ряда свойств с известного явления на неизвестное явление.

1. метод индукции;

2. метод аналогии;

3. метод дедукции;

4. позитивный анализ

Установите соответствие между отдельными методами и приемами исследования экономики

1. Метод анализа

2. Метод дедукции

3. Метод экономико-математического моделирования

4. Метод аналогии

а) познание, предполагающее перенос свойств с известного экономического явления на неизвестное;

б) познание, предполагающее разделение целого на отдельные составные части и изучение каждой из этих частей;

в) формализованное описание экономического явления с помощью математического аппарата;

г) познание, предполагающее умозаключение от общего к частному.

7. К характеристике экономических законов не относится то, что они…

а) познаваемы;

б) носят объективный характер;

в) создаются людьми;

г) действуют только в экономических системах.

В чем заключается единство законов природы и общества:

а) носят объективный характер;

б) не зависят от деятельности людей;

в) проявляются через экономическую деятельность людей;

г) носят исторически приходящий характер;

д) являются вечными.

Экономическая теория изучает

а) производство благ и услуг;

б) ограниченные ресурсы;

в) экономическое поведение людей;

г) способы удовлетворения потребностей.

Установите соответствие между отдельными приемами и методами исследования экономики.

1. Отвлечение от несущественного, неглавного;

2. Разделение явления на отдельные составные части;

3. Формулировка вывода на основе отдельных факторов;

4. Формализованное описание экономического процесса;

а) метод экономико-математического моделирования;

б) метод анализа;

в) метод научной абстракции;

г) метод индукции.

Познавательная функция экономической теории проявляется в

а) познании сущности экономических явлений, объективных законов экономического развития;

б) разработке методов и средств научного инструментария, необходимых для исследований всем экономическим наукам;

в) обеспечении экономической политики;

г) разработке научных прогнозов и перспектив экономического развития.

Вопросы для обсуждения

1. Что является предметом изучения экономической теории

2. Охарактеризуйте историю развития предмета экономической теории

3.Назовите основные функции экономической теории и дайте их характеристику

4. Охарактеризуйте основные разделы экономической теории

5. Что такое экономические законы.

6. Что общего между экономическими законами и законами природы? Чем они отличаются?

7. В чем особенность традиционной экономической системы? В каких странах используется традиционная экономическая система?

8. Охарактеризуйте Китайскую модель смешанной экономики?

9. В чем состоит Японское экономическое чудо?

10. Какие виды теневой экономики выделяет экономическая теория? Дайте их характеристику.

11. В чем состояла особенность первого этапа приватизации в России?

Глоссарий

Потребность - это нужда в чем-либо необходимом для поддержания жизнедеятельности, развития личности и общества в целом

Благо – это материальные (товары) и нематериальные (услуги) продукты природы и человеческой деятельности, которые прямо или косвенно служат удовлетворению человеческих потребностей

Экономическое благо – это благо, потребность в котором превышает его наличие в данный период времени

Ресурсы – это все то, что используется на производство товаров и услуг

Труд – это физические и умственные усилия людей, направленные на создание или преобразование материальны и нематериальных благ

Земля – производственная площадь, необходимая для производственного процесса.

Инвестиционные ресурсы включают в себя производственные площади, энергетические мощности, систему складских и транспортных средств, сеть сбытовых организаций

Кривая производственных возможностей – это кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены при полном или наиболее эффективном использовании ресурсов и неизменной технологии

Альтернативные издержки – это оценка наиболее ценной из отвергнутых в результате выбора возможностей использования данного ресурса, эта цена, измеряемая через другую вещь, которую нужно отдать взамен

Задача 1.

Построить кривую производственных возможностей, если на производство 1 тыс. станков необходимо столько же ресурсов, сколько на производство 2,5 млн. кг масла. Общее количество ресурсов позволяет производить либо 25 млн. кг масла либо 10 тыс. станков.

Шкала производственных возможностей

Вариант	Масло, млн. кг	Станки, тыс. шт.
A	25
B	20
C	15
D	10
E	5
F	0

Задача 2.

Построить кривую производственных возможностей, если для увеличения производства масла на 1 млн. кг необходимо снизить производство компьютеров на 0,8 тыс. шт. отметить на ней область недоиспользования ресурсов. Максимальный объем производства компьютеров при наличии ресурсов 16 тыс. шт.

Шкала производственных возможностей

Вариант	Масло, млн. кг	Компьютеры, тыс. шт.
A	0
B	3
C	7
D	9
E	12
F	14

Задача 3.

Построить кривую производственных возможностей, если на производство 1 тыс. компьютеров необходимо столько же ресурсов, сколько для производства 2 млн. кг сыра. Отразить на графике область недоиспользования ресурсов. Полное использование ресурсов позволяет максимально производить либо 10 тыс. компьютеров либо 20 млн. кг сыра.

Задача 4.

Построить кривую производственных возможностей, если на производство 1 тыс. шт. пушек необходимо столько же ресурсов, сколько для производства 1,5 млн. кг сыра. Полное использование ресурсов позволяет максимально производить либо 10 тыс. пушек либо 15 млн. кг сыра.

Задача 5.

Рассчитать альтернативный объем производства, если на производство 1 тыс. компьютеров и 1,7 млн. кг масла затрачивается одинаковое количество ресурсов. При имеющихся ресурсах максимальный объем производства составляет 34 млн. кг масла или 20 тыс. шт. компьютеров. Построить кривую производственных возможностей.

Задача 6.

Определите альтернативную стоимость компьютера, если известно, что на производство одного компьютера уходит столько же средств, сколько на производство двух магнитофонов.

Задача 7.

Определите альтернативную стоимость 7 млн. кг масла, если для его производства необходимо снизить производство компьютеров на 4 тыс. шт. Стоимость 1 тыс. компьютеров 18 млн. руб.

Задача 8.

Рассчитать альтернативную стоимость масла при каждом варианте использования ресурсов, если на производство 1 тыс. компьютеров и 1,4 млн. кг масла затрачивается одинаковое количество ресурсов. При имеющихся ресурсах максимальный объем производства составляет либо 28 кг масла, либо 20 тыс. компьютеров. Стоимость 1 тыс. компьютеров 18,7 млн. руб.

Задача 9.

Рассчитать альтернативную стоимость масло при каждом варианте использования ресурсов, если стоимость 1 тыс. станков 14,3 млн. руб.

Шкала производственных возможностей

Вариант	Масло, млн. кг	Станки, тыс. шт.
A	0	9
B	3	7
C	7	5
D	9	3
E	12	1
F	14	0

Задача 10.

Построить кривую производственных возможностей, если на производство 1 тыс. шт. станков необходимо столько же ресурсов, сколько для производства 1,5 млн. кг сыра.

Шкала производственных возможностей

Вариант	Масло, млн. кг	компьютеры, тыс. шт.
A	25
B	23
C	18
D	11
E	5
F	0

Задача 11.

Фермер производит два вида продукции: молоко и мясо. Производственные возможности описаны в таблице

Вид продукции	Производственные альтернативы
Вид продукции	A	B	C	D	E
Молоко, млн. л	0	1	2	3	4
Мясо, тыс. т	10	9	7	4	0

Постройте кривую производственных возможностей. Как изменится ее положение, если в результате внедрения новых рационов питания животных производительность в производстве молока увеличится в 1,5 раза?

Задача 12.

Кривая производственных возможностей фирмы задана уравнением 2Q_A + 5Q_B = 1000. Определить, как изменится альтернативная стоимость производства товаров А и В при увеличении производственных возможностей фирмы на 40% если цены товаров соответственно равны Р_А = 50 – 0,02 Q_A, Р_В = 50 – 0,02 Q_В.

Задача 13.

Кривые производственных возможностей двух фирм заданы уравнениями Q_A + 5Q_B = 300, 2Q_A + 8Q_B = 400. Построить кривую совокупных производственных возможностей и найти альтернативную стоимость производства товаров А и В на всех возможных интервалах изменения объемов выпуска, если цены товаров, соответственно равны Р_А = 500 – 0,5 Q_A, Р_В = 400 – Q_В.

Задача 14.

Кривые производственных возможностей трех фирм, работающих в данной производственной, сфере заданы уравнениями Q_A + 5Q_B = 300, 2Q_A + 8Q_B = 400, 3Q_A + 6Q_B = 600. Построить кривую совокупных производственных возможностей и найти альтернативную стоимость производства товаров А и В на всех возможных интервалах изменения объемов выпуска, если цены товаров, соответственно равны Р_А = 400 – 0,5 Q_A, Р_В = 300 – Q_В.

Задача 15.

Кривые производственных возможностей двух цехов фирмы, производящей товары А и В, заданы уравнениями 3Q_A + 5Q_B = 300, 2Q_A + 4Q_B = 300. Фирма получила заказ на производство 200 единиц товара А. Найти максимальное количество товара В, которое сможет произвести фирма после выполнения заказа. Построить кривую совокупных производственных возможностей фирмы.

Тестовые задания

Вопросы для обсуждения

1. Что такое экономические блага?

2. Чем благо отличается от ресурса?

3. Каким признаком обладают ресурсы? Почему?

4. Что показывает каждая точка на кривой производственных возможностей, выше и ниже данной кривой?

5. Что такое альтернативные издержки?

6. Назовите характерные особенности альтернативных издержек.

7. Что такое потребность, и какими они бывают?

РАЗДЕЛ II . МИКРОЭКОНОМИКА

Глоссарий

Спрос – D (от англ. demand) - это желание и способность покупателей совершать сделки по приобретению имеющихся на рынке товаров.

Действительный спрос – реально предъявляемый спрос на товары и услуги.

Реализованный спрос – часть действительного спроса, которая реализована на рынке в купленных товарах и услугах.

Неудовлетворенный спрос – нереализованная часть действительного спроса в виду отсутствия нужных товаров или несоответствия их ассортимента и качества требованиям покупателей.

Уравнение кривой спроса

Q_d = a - b * P

где: Q_d – величина спроса при заданном уровне дохода;

a – параметр, показывающий минимальный объем спроса, независящий от уровня цены;

b – параметр, показывающий реакцию величины спроса на изменение цены;

P – цена.

b = ΔQ/ΔP

Закон спроса: если цена какого-либо товара повышается (при этом все другие условия остаются неизменными), то спрос будет предъявляться на меньшее количество этого товара

Предложение – S (от англ. supply) - это желание и способность производителей предлагать для реализации на рынке определенные блага.

Дуговая эластичность

Ep = [( Q ₂ – Q ₁ ) / ( P ₂ – P ₁ )] * [( P ₂ + P ₁ ) / ( Q ₂ + Q ₁ )]

Задача 1.

При понижении цены на огурцы с 6 до 5 руб. за 1 кг объем продаж увеличился с 300 до 350 кг в день. Найти аналитический вид функции спроса, если она линейная.

Задача 2.

Дана функция спроса на масло: Q_d = 800 - 10P. Как изменится ее вид, если:

а) в результате повышения уровня доходов потребителей величина спроса возросла на 20% при каждом уровне цены.

б) в результате повышения уровня дохода потребителей цена спроса возросла на 10% при каждом объеме покупок.

Задача 3.

Дана функция предложения Q_s = 50P – 100. Найдите, как изменится ее вид, если:

а) величина предложения увеличится на 10% при каждом уровне цен;

б) цена предложения увеличится на 20% при каждом объеме продаж;

в) величина предложения уменьшится на 40% при каждом уровне цен;

г) цена предложения уменьшится в 2 раза при каждом объеме продаж.

Задача 4.

Уравнение кривой спроса имеет вид Pd = -2Q + 100. Найти новое уравнение, если увеличение цены товара субститута привело к изменению спроса на 20%.

Задача 5.

Уравнение кривой спроса имеет вид Pd = -5Q + 80. Найти новое уравнение, если увеличение цены товара комплимента привело к изменению спроса на 10%.

Задача 6.

При увеличении стоимости яблок с 4 до 6 руб. за кг величина спроса изменилась со 100 до 70 кг в день. Определите, какое количество яблок сможет продать продавец по цене 5 руб. за кг в течение двух дней и какую цену должен назначить продавец, желающий продать 90 кг яблок в течение одного дня. Функция спроса линейная.

Задача 7.

При увеличении цены товара с 5 до 10 руб. величина спроса уменьшилась со 100 до 50 штук в день. Функция спроса линейная. Найти:

а) какое максимальное количество товара может быть реализовано на этом рынке;

б) максимальную цену, при которой продавец не сможет продать ни одной единицы товара;

в) какое количество товара может реализовать продавец по цене 7 руб.

г) какую цену должен установит продавец, желающий реализовать 70 штук в течение дня.

Задача 8.

При увеличении цены товара с 8 до 16 руб. величина предложения увеличилась с 2 тыс. штук до 16 тыс. штук в день. Определить какое количество товара сможет приобрести покупатель по цене 10 руб. в течение двух дней и какую цену должен предложить покупатель, желающий приобрести 20 тыс. штук товара.

Задача 9.

На рисунке показаны кривые спроса (D) и предложения (S) на сигареты в городе Вилинсси.

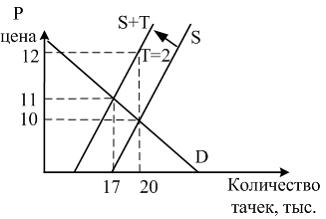
Мэрия города в целях борьбы за здоровый образ жизни установила налог (Т) на продажу сигарет в 2 лиры за пачку. К чему это приведет.

Задача 10.

Коэффициент эластичности спроса по цене равен E_p^d = - 0,3, предложения E_p^s = +0,4. При рыночном равновесии потребляется 20 единиц блага по цене 4 ден.ед. Вывести функции спроса и предложения в аналитическом виде, при условии, что они линейные.

Задача 11.

Функция спроса населения на данный товар Qd =7- Р, функция предложения данного товара: Qs= -5+2Р. Определите равновесную цену и равновесный объем продаж. Что случится, если цена будет установлена на уровне 3 руб.?

Задача 12.

Функция спроса населения на данный товар Qd =10 – Р, функция предложения данного товара: Qs= -5+2Р. Предположим, что на данный товар установлена фиксированная цена на уровне 3 ден. ед. Определить объем неудовлетворенного спроса.

Задача 13.

Функция спроса задана уравнением Qd = 50 - 2P, а функция предложения Qs = 3P - 5. Чему равен излишек потребителя.

Задача 14.

Функция спроса на данный товар Qd =8 – Р, функция предложения данного товара: Qs= -7+2Р. Определить излишек производителя.

Задача 15.

На рисунке показаны кривые спроса (D) и предложения (S) на мясо в провинции Вилабаджи.

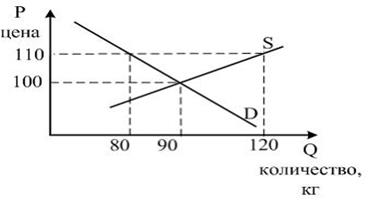
Охарактеризуйте ситуацию на рынке, если власти провинции для поддержки местных фермеров решат установить фиксированную цену 110 су за кг.

Задача 16.

Функция спроса на данный товар Qd = 4 – Р, функция предложения данного товара: Qs=-6+4Р. Предположим, что государство установило фиксированную цену на данный товар:

а) в 3 ден. ед. за единицу товара;

б)1,5 ден. ед. за единицу товара.

Определить избыток спроса и избыток предложения, а также реальный объем продаж в состоянии равновесия и при фиксированных ценах. В каком из указанных случаев объем потребления будет наибольшим?

Задача 17.

Ситуация на рынке такова, что при цене в 10 ден. ед. покупатели готовы купить 40 штук гвоздик, а продавцы согласны были продать 10 штук гвоздик; по цене 20 ден. ед.- соответственно 30 и 20 штук; по цене 30 ден. ед. – 20 и 30 штук и. наконец, по цене в 40 ден. ед.- 10 и 40 штук.

1. Определить функцию спроса и предложения от цены.

2. Определить равновесную цену и объем продаж.

Задача 18.

Кривая спроса на стулья описывается уравнением Qd =60 – 2Р, а кривая предложения стульев Qs= 30+ 4Р. Определить равновесную цену и равновесный объем продаж.

Задача 19.

Спрос и предложение в студенческой столовой описываются уравнениями: Qd =1200 – 20Р; Qs=-200+50Р. Вычислите параметры равновесия. Определить дефицит обедов и снижение излишков продавца, если администрация установила цену на уровне 15 руб. за обед.

Задача 20.

Кривая предложения описывается уравнением: Qs =-400 + 200Р. Равновесна цена 4 долл. При цене 6 долл. возникает излишек товара в размере 600 ед. Определить:

а) вид функции спроса при условии, что зависимость величины спроса от цены линейная;

б) излишек продавцов и покупателей, если рынок находится в состоянии равновесия.

Задача 21.

Уравнение кривых спроса и предложения имеют вид P_d = -0,5Q + 50, P_s = 2Q + 8. Определить на сколько процентов изменится равновесная цена и равновесный объем продаж товара, если увеличение цены товара комплимента привело к изменению спроса на 30%.

Задача 22.

При повышении цены блага с 10 руб. до 20 руб. величина предложения изменилась с 7 шт. до 20 шт., а величина спроса с 15 шт. до 5 шт. Определить ситуацию на рынке, если продавец установит цену на 10% выше равновесной. Функция спроса и предложения линейные.

Задача 23.

Кривая предложения описывается уравнением: Qs =-600 + 300Р. Равновесна цена 5 долл. При цене 7 долл. возникает излишек товара в размере 700 ед. Определить:

а) вид функции спроса при условии, что зависимость величины спроса от цены линейная;

б) излишек продавцов и покупателей, если рынок находится в состоянии равновесия.

Задача 24.

Уравнения кривых предложения двух фирм, работающих на одном рынке, имеют вид: вид P_s₁ = 2Q + 200, P_s₂ = 2Q + 100. На этот же рынок выходят два покупателя, кривые индивидуального спроса каждого из которых задаются уравнениями: P_d₁ = -5Q + 800, P_d₂ = -5Q + 600. Найти, как изменится равновесная цена и равновесный объем продаж, если спрос со стоны второго покупателя снизится на 20%.

Задача 25.

Функция спроса на товар задана уравнением Qd = 50 – 2P, а функция предложения – Qs = 3P + 5. Определить излишек потребителя.

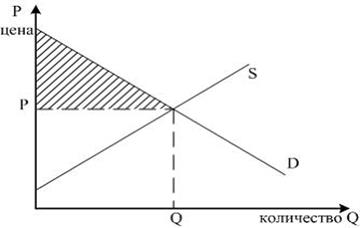
Задача 26.

Дана функция рыночного спроса и предложения: Qd = 80 – 10Р Рs = 0,1Qs + 2. Определите равновесную цену и равновесный объем продаж после того, как:

а) величина спроса увеличится на 10% при каждом уровне цен;

б) величина спроса уменьшится на 10 единиц при каждом уровне цен

в) цена спроса увеличится на 2 руб. при каждом объеме спроса;

г) цена спроса уменьшится на 20% при каждом объеме спроса.

д) величина предложения увеличится на 5 единиц при каждом уровне цен;

е) цена предложения сократилась на 10% при каждом уровне цен;

ж) величина предложения возросла на 20% при каждом объеме предложения;

з)цена предложения сократилась на 1 руб. при каждом объеме предложения.

Задача 27.

Кривые спроса и предложения товара задаются уравнениями: Рd = -2Q +200, Ps = 2Q+10. Определить, на сколько процентов изменяться равновесные цена и объем, если правительство вводит налог с производителя по ставке 10% от стоимости товара.

Задача 28.

Уравнение кривых спроса и предложения имеют вид: Рd = -0, 05Q + 450, Ps = 0,03Q+50. Определить, на сколько процентов изменяться равновесные цена и объем, если правительство вводит налог с покупателя в размере 20 руб. с каждой единицы товара.

Задача 29.

Зависимость величины спроса на товар А от цены товара В задается уравнением Q_dA = 80P_B – 0,5P²_B. Найти значение перекрестной эластичности спроса на товар В по цене товара А.

Задача 30.

В таблице представлена зависимость объема спроса от цены товара. Используя формулу дуговой эластичности вычислить показатели эластичности спроса по цене для каждого отрезка.

Цена 1 кг яблок, руб.	Покупатели готовы купить, кг
100	1
90	2
80	3
70	4
60	5

Задача 31.

Определить коэффициент прямой и перекрестной эластичности, если цена товара А увеличилась с 37 до 42 ден. ед., а цена товара В снизилась с 47 до 39 ден. ед., в результате спрос на товар А изменился со 157 до 143 ед.

Задача 32.

Функция спроса на товар Q_d = 8 – P_,а функция предложения Qs=-7+3Р. Определить равновесную цену и равновесный объем. При увеличении цены на 3 ден. ед. определить эластичность спроса и эластичность предложения.

Задача 33.

Функция спроса задана таблично. Найти эластичность в каждой точке и на отрезке между ними.

Р, ден.ед.	12	6	4
Q_D, шт	6	8	10

Задача 34.

Дана некая функция спроса. В точке (Р₀,Q₀) эластичность E_p^d = - 1. Как измениться эластичность:

1. при Р = Р₀, если спрос увеличится в два раза;

2. при Q = Q₀, если функция спроса сдвинется на +Р.

Задача 35.

Если эластичность спроса по цене на видеокамеры равна (-3), то какое будет процентное изменение величины спроса на них, если известно, что цена выросла на 10% ?

Задача 36.

По цене 10 руб. первый покупатель приобретает 100 штук товара, эластичность спроса по цене в точке равна -2. Второй покупатель приобретает 200 штук, эластичность спроса по цене в точке равна -4. Функции спроса линейные. Найти эластичность рыночного спроса в точке:

а) соответствующей данному значению цены;

б) соответствующей объему спроса 100 штук;

в) соответствующей объему спроса 40 штук.

Задача 37.

На рынке по цене 50 руб. в течение дня продается 100 единиц товара. Найти какую цену должен назначить продавец, рассчитывающий продать товар на сумму 2500 руб., если значение эластичности спроса по цене в начальной ситуации равно – 2. функция спроса является линейной.

Задача 38.

Цена товара выросла с 3000 руб. до 3600 руб. При этом величина спроса на него снизилась в 1,2 раза. Найти значение ценовой эластичности.

Задача 39.

Функция спроса задается уравнением Qd = 20 – 10P + P². Найти значение ценовой эластичности спроса при цене Р = 1.

Задача 40.

Функция спроса задается уравнением Qd = 35 – 15P + 2P². Найти значение ценовой эластичности спроса при цене Р = 2.

Тестовые задания

1. Спрос и предложение на молоко записаны при помощи уравнений: Qd = 20 – 2 P , Qs = -10 + 4 P . В результате введения фиксированного уровня цен на молоко имело место его перепроизводство в объеме 12 пакетиков. Цена на молоко была зафиксирована государством на уровне:

а) 3 руб.;

б) 8 руб.;

в) 7 руб.;

г) 5 руб.

2. При повышении цены товара на 18%, спрос на него снизился на 20%. Это означает, что коэффициент ценовой эластичности спроса равен:

а) коэффициент 9/10 спрос эластичный;

б) коэффициент 10/9 спрос эластичный;

в) коэффициент 10/9 спрос неэластичный;

г) коэффициент 9/10 спрос неэластичный.

Закон спроса утверждает что

а) люди готовы покупать больше товаров, когда их доходы растут;

б) превышение величины предложения над величиной спроса приводит к нехватке товаров;

в) по более высокой цене люди готовы купить меньшее количество товара;

г) спрос всегда определяет предложение товара.

Вопросы для обсуждения

1. В чем смысл эффекта сноба и эффекта Веблена?

2. С помощью каких факторов может быть объяснена конфигурация кривой спроса? Какие характерные особенности имеет кривая спроса?

3. Что такое перекрестная эластичность? Назовите основные её формы и дайте их характеристику.

4. Какие модели эластичности спроса и эластичности предложения выделяет неоклассическая теория?

5. Какие виды спроса различают в современной экономической теории?

6. Какие характерные особенности имеет кривая предложения?

7. Что такое рыночное равновесие. Что является координатами точки равновесия?

8. Под влиянием каких факторов происходит сдвиг кривой предложения и перемещение по кривой предложения?

Глоссарий

Полезность – это степень удовольствия, получаемая потребителем от потребления набора товаров и услуг. Различают общую и предельную полезность.

Предельная полезность (MU)– это дополнительная полезность, полученная от потребления последующей единицы данного блага по сравнению с предыдущей.

MU =∆ TU /∆ Q_X

где: MU – предельная полезность

TU – общая полезность данного товара

Q_X – потребление товара

Функция предельной полезности: MU = ( TU )’

Общая (совокупная) полезность ( TU ) – это совокупная полезность от потребления всех наличных единиц блага

( TU = ∑ MU )

Условие равновесия потребителя имеет вид:

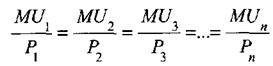
Оптимальный потребительский выбор определяется путем решения системы уравнений

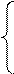MUx/Px = MUy/Py

I=P_x*Q_x +P_y*Q_y

Кривая безразличия – это кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.

Закон убывающей предельной полезности: по мере увеличения количества потребляемого товара его предельная полезность имеет тенденцию к сокращению.

Бюджетная линия – это геометрическое место точек, представляющие собой доступные потребителю наборы товаров х и у при неизменных ценах и фиксированном доходе.

Задача 1.

Заполнить пропуски в таблице.

Количество товаров	А		В		С
Количество товаров	TU	MU	TU	MU	TU	MU
1		20	19		22
2		15	30			10
3		12	38		39
4		8	43		44
5		6	45			3

Задача 2.

Предельная полезность первой единицы блага равна 420. При потреблении первых трех единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единиц блага при дальнейшем потреблении падает в 4 раза. Найти общую и среднюю полезность блага при условии, то его потребление составляет 8 единиц.

Задача 3.

Функция общей полезности, получаемой при потреблении товара, задается уравнением TU = 100Q + 150Q² – 2Q³. Найти значение предельной полезности пятой единицы товара.

Задача 4.

Потребитель тратит 13 ден.ед. в неделю на помидоры и огурцы. Предельная полезность помидор для него определяется уравнением: 30 – 2х, где х – количество помидор в кг. Предельная полезность огурцов представлена уравнением: 19 – 3у, где у –количество огурцов в кг. Цены товаров соответственно 2 и 1 ден.ед. Какое количество помидор и огурцов приобретёт рациональный потребитель?

Задача 5.

Потребитель расходует 20 руб. в день на лимонад и мороженное. Цена лимонада равна 10 руб. за литр, а цена мороженного 2,5 руб. за 100-граммовую порцию. Известны функции совокупной полезности лимонада и мороженного с его точки зрения. Для лимонада: TU(Q) = 30Q – 5Q² и TU(Q) = 25Q – 2,5Q²– для мороженного. Какое количество лимонада и мороженного принесет потребителю максимум удовлетворения в рамках данного денежного ограничения?

Задача 6.

Потребитель расходует в неделю 49 руб. на бананы и яблоки. Предельная полезность банана для него равна 65 -5х, где х – количество бананов. Предельная полезность яблока равна 100 – 12y, где y – количество яблок. Цена 1 банана составляет 5 руб., цена одного яблока - 8 руб. Определите:

а) какое количество бананов и яблок купит рациональный потребитель;

б) как изменится поведение потребителя, если его доход возрастет, и он решит тратить на фрукты 80 руб. в неделю.

Задача 7.

Функция полной полезности от потребления товаров А,В и С представлена уравнением: TU= 6Q_A + 8Q_B + 4Q_C. Цена товара В равна 4 рублям. Найти значения цен товаров А и С, если известно, что потребитель находится в состоянии потребительского равновесия.

Задача 8.

В таблице представлена полная и предельная полезность потребления блага А. Цена блага А составляет 4 руб.

Количество блага А	Предельная полезность	Полная полезность	Относительная полезность
1		25
2		48
3	20
4		85
5	13
6	8
7		108
8	0

а) заполнить таблицу, рассчитав недостающие данные;

б) какое количество блага А приобретет рациональны потребитель, если предельная полезность блага В при условии равновесия потребления составляет 35 ютилей, а цена блага В равна 7 руб.

Задача 9.

Рациональный потребитель стремится максимизировать полезность потребления двух товаров А и В с учетом средств, которые он может направить на потребление этих товаров. Взаимосвязь между товарами А и В задается функцией: Q_B = 63/(Q_A+3) + 2. Количество обоих товаров измеряется целыми числами. Цена единицы товара А относится к цене товара В как 5 к 4. Потребитель определил для себя ту сумму, которую он готов потратить на покупку товаров А и В. Если эта сумма была бы полностью потрачена на покупку только товара В, потребитель смог бы купить 16 единиц этого товара.

Определите выбор потребителя, отобразите ситуацию графически.

Задача 10.

Предельная полезность товара А равна 100, цена товара А равна 10. Цена товара В равна 5. Определить предельную полезную товара В в состоянии потребительского равновесия.

Задача 11.

Для потребителя товар А по цене 0,7 ден.ед. приносит удовлетворение в размере 10 ютилей. Какую полезность в ютилах принесёт ему потребление товара В по цене 0,5 ден.ед. в положении равновесия?

Задача 12.

Семья покупает каждый день два товара А и В. Цена товара А равна 0,6 ден.ед., товара В – 1ден.ед. На данный момент семья покупает такое количество этих товаров, что предельная полезность их последних единиц равна соответственно 40 и 50 ютилей. Можно ли сказать, что покупается набор, который приносит наибольшее удовлетворение? Если нет, то каким образом необходимо перераспределить расходы между двумя этими товарами?

Задача 13.

Индивид, получающий доход 900 ед., потребляет два блага в количествах X и Y, его предпочтения описываются функцией полезности ТU = XY³. Найти набор благ, потребляемый индивидом при ценах PX = 5, PY = 12.

Задача 14.

Функция полезности потребителя имеет вид U = XY, его доход I = 36, а цены товаров Px = 4, Py = 6. Определить полезность оптимального потребительского набора.

Задача 15.

Индивид потребляет 5 шт. товара А, приносящего ему 8 ед. полезности и 12 шт. товара Б, дающего 18 ед. полезности. Он решил, что ничего не произойдёт, если он будет потреблять 7 шт. товара А и 10 шт. товара Б, которые принесут ему, соответственно 10 и 16 ед. полезности. Определить величину предельной полезности для каждого товара и предельную норму замещения товаров.

Задача 16.

Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имеет доход 100 ден. ед. Найти цены товаров Х и Y, если известно, что предельная норма замены товара Х товаром Y равна 4.

Задача 17.

Определить предельную норму замещения одного товара другим для каждого набора товаров.

Набор товаров	Цена товара А	Цена товара В
A	37	4
B	33	11
C	28	15
D	21	23
E	19	34

Задача 18.

Потребитель покупает в магазине мясо и сыр. Он может комбинировать их количество в таких соотношениях

Комбинации	Мясо (кг)	Сыр (кг)
А	4	0,5
Б	2,5	1
В	1,5	1,5
Г	1	2,5

Определить предельные нормы замены мяса сыром.

Задача 19.

Функция общей полезности индивида от потребления блага Х имеет вид: TU_x = 40Q_x– Q_x², а от потребления блага Y -TU_y = 18Q_y – 4Q_y². Он потребляет 10 единиц блага Х и 2 единицы блага Y. Предельная полезность денег составляет 0,5. Определите цены товаров X и Y.

Задача 20.

Индивид покупает 8 единиц товара Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.

Задача 21.

Вы можете купить «Пепси» и «Фанту», при этом больше 5 бутылок Вам не выпить. Вы оцениваете для себя полезность напитков так, как представлено в таблице. Что Вы будете пить и в каком количестве, максимизируя полезность?

Количество напитков	Полезность
Количество напитков	«Пепси»	«Фанта»
1	15	10
2	28	19
3	38	25
4	46	28
5	51	30
6	55	31

Задача 22.

Потребитель делает выбор между двумя товарами А и В. Предельная полезность каждого приведена в таблице. Какое количество каждого товара купит рациональный потребитель, если его бюджет равен 50 ден.ед., а цена товара А равна 10 ден.ед., В – равна 5 ден.ед.

Количество товара	Товар А	Товар В
1	35	20
2	30	15
3	20	14
4	10	10
5	1	1

Задача 23.

На рисунке показана кривая безразличия и бюджетная линия некоего потребителя.

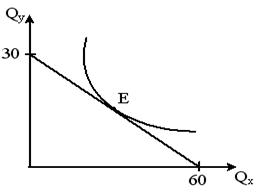
Напишите уравнение бюджетной линии, если цена товара Y равна 4 рублям.

Задача 24.

На рисунке показана кривая безразличия и бюджетная линия некоего потребителя. Напишите уравнение бюджетной линии, если цена товара Y равна 10 рублям.

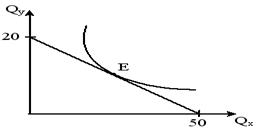
Задача 25.

Допустим, потребитель имеет доход 300 ден. ед. в месяц и он весь должен быть израсходован на покупку двух товаров: товара Х ценой 3 ден. ед. за штуку и товара Y ценой 5 ден. ед. за штуку. Напишите уравнение бюджетной линии.

Задача 26.

На графике показана бюджетная линия. Цена товара А 18 руб. Определить, какова цена товара В. Как изменится положение бюджетной линии при увеличении цены товара А до 30 руб. и при ее снижении до 15 руб.?

Задача 27.

Построить бюджетную линию при уровне дохода 150 руб., если стоимость 1 кг. апельсинов 15 руб., а 1 кг. яблок – 10 руб. Отразить перемещение бюджетной линии при снижении дохода до 120 руб. и при увеличении дохода до 180 руб.

Задача 28.

Доход потребителя составляет 200 ден. ед. в неделю. Он приобретает только два вида благ: пельмени и молоко. Одна пачка пельменей стоит 5 ден. ед., а 1 литр молока – 3 ден. ед. Напишите уравнение бюджетного ограничения.

Задача 29.

Предположим, что недельный доход потребителя равен 40 ден.ед. и он расходует его на хлеб и молоко.

а) при условии, что цена 1 буханки хлеба 4 ден. ед. (Х), а цена 1 литра молока 10 ден. ед. (Y), напишите уравнение бюджетной линии.

б) как изменилось бы уравнение бюджетной линии, если бы доход потребителя уменьшился до 20 дед. ед.

Задача 30.

На графике дана бюджетная линия потребителя, которому необходимо приобрести два товара. Цена товара А равна 0,8 ден.ед., цена товара В равна 0,4 ден.ед.

Определить:

1. бюджет потребителя;

2. точку на графике, в которой потребитель может купить только товар А;

3. точку на графике, в которой не будет использован весь бюджет;

4. точку на графике (3 единицы товара А и 7 единиц товара В). Что можно сказать про такой набор товаров?

Задача 31.

Цена продукта А равна 1ден.ед., цена продукта В равна 2 ден.ед., доход потребителя – 18 ден.ед. Набор безразличия двух товаров задан таблично:

Товар А	16	12	8	4
Товар В	6	8	12	24

Построить бюджетную линию и кривую безразличия. Определить точку равновесия потребителя, наклон бюджетной линии, предельную норму замещения.

Тестовые задания

1. Общая полезность растет, когда предельная полезность:
а) увеличивается или уменьшается, но является величиной положительной;
б) уменьшается;
в) увеличивается;
г) увеличивается в медленном темпе.

Предельная полезность – это

а) максимальный уровень полезности, который хочет получить потребитель;

б) полезность, которую потребитель получает от потребления дополнительной единицы блага;

в) максимальная полезность, которую можно получить при потреблении данного количества блага;

г) максимальный уровень полезности, который можно достигнуть при расходовании данной суммы денег;

д) минимальный уровень полезности, которую получает потребитель.

Предельная норма замещения:

а) всегда положительна;

б) представляет собой отношение предельных полезностей товаров-заменителей;

в) показывает, от какого количества одного блага потребитель должен отказаться для приобретения единицы другого блага так, чтобы уровень общей полезности не изменился;

г) характеризует наклон бюджетной линии.

Глоссарий

Производственный процесс – это способ соединения факторов производства с целью их превращения в конечные товары и услуги

Производственная функция – функциональная взаимосвязь, отображающая зависимость между вводимой комбинацией факторов производства и объемом выпуска продукции

Изокванта – кривая, показывающая все возможные комбинации производственных факторов, которые обеспечивают постоянный (одинаковый) объем выпуска продукции

Изокоста – линия, объединяющая все возможные сочетания ресурсов, которые имеют одинаковую суммарную стоимость

Предельная норма технологического замещения – показатель пропорции, в которой должна происходит замена одного фактора производства другим при сохранении неизменного объема выпуска

MRTS_KL = - ∆K/∆L = MP_L/MP_K,

где: MP_L – физический объем предельного продукта труда;

MP_K - физический объем предельного продукта капитала.

MRTS_KL = P_L / P_K

где: P_L - цена единицы труда;

P_K - цена единицы капитала.

Общий продукт (ТР) – это суммарный объем выпуска продукции, полученный в рамках заданной производственной функции, и измеренный в физических единицах

Предельный продукт фактора производства (МР_L₎, исчисленный в физических единицах, показывает изменение в объеме выпуска продукции, вызванное использованием дополнительной единицы данного фактора (L) при неизменном количестве всех остальных

МР _L =∆ Q /∆ L

где МР_L - предельный продукт фактора L;

∆Q – изменение общего объема выпуска продукции;

∆L – изменение количества фактора L.

Средний продукт фактора (AP_L) определяется путем деления объема выпускаемой продукции на количество используемого переменного фактора.

AP_L = Q / L

Правило использования ресурсов: МRР = МRС

Правило наименьших издержек: последний рубль, затраченный на каждый ресурс, должен давать одинаковый предельный продукт.

Равновесие производителя – состояние производства (сочетание факторов), когда рубль, потраченный на любой из факторов производства, дает одну и ту же отдачу, или предельная норма технологического замещения факторов равна соотношению цен этих факторов.

Условие равновесия производителя:

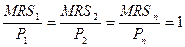, или ,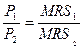

Закон убывающей предельной производительности факторов производства: по мере увеличения количества переменного фактора при неизменном количестве всех остальных факторов будет достигнут такой рубеж, после которого предельный продукт переменного фактора начнет уменьшаться

Отдача от масштаба - взаимосвязь между изменением масштаба производства и соответствующим изменением в объеме выпуска продукции называется

Постоянная отдача от масштаба - при пропорциональном увеличении количество факторов в n раз, объем производства тоже возрастет в n раз, то имеет место постоянная отдача от масштаба, т.е. Q₂ = n Q₁(где Q₁– первоначальный объем производства)

Возрастающая отдача от масштаба - в случае, когда пропорциональное увеличение всех применяемых факторов в n раз вызовет рот объема производства больше, чем в n раз, наблюдается возрастающая отдача от масштаба, т.е. Q₂ > n Q₁

Уменьшающаяся отдача от масштаба - когда пропорциональное увеличение всех переменных факторов в n раз вызывает рост объема производства меньше, чем в n раз, имеет место убывающая отдача от масштаба, т.е. Q₂ < n Q₁.

Задача 1.

Определить предельный и средний продукты.

Количество используемого труда	1	2	3	4	5	6
Совокупный продукт	35	80	122	156	177	180

Задача 2 .

Найдите величину совокупного продукта, если известны:

Затраты рабочего времени	1	2	3	4	5	6	7
Предельный продукт	2	3,5	5	7	4,5	3	1

Задача 3.

Заполните пропуски в таблице.

Количество используемого труда	Общий продукт	Средний продукт	Предельный продукт
3		20	-
4	80
5			10
6	95

Задача 4.

Заполните таблицу, внося недостающие цифры.

Количество используемого труда	Общий продукт	Средний продукт	Предельный продукт
1	7
2	14
3			8
4			1
5		3,2

Задача 5.

Дана производственная функция имеет вид Q = 21*L+9L²-L³+2. Рассчитайте предельный продукт труда при использовании 3, 5 и 7 единиц труда.

Задача 6.

Определить средний и предельный продукт

Затраты труда	Затраты капитала	Объем выпуска	Средний продукт труда	Предельный продукт труда
0	10	0
1	10	10
2	10	30
3	10	60
4	10	80
7	10	112
8	10	112
9	10	108

Задача 7.

Для производственной функции Кобба-Дугласа Q =К^1/2L^1/2 предельная норма технологического замещения капитала трудом увеличилась на 15%. Определите, как изменится соотношение L/К, если первоначально оно составляло 3, а эластичность замены капитала трудом равна 0,3.

Задача 8.

Производственная функция фирмы имеет вид: Q (х, у) = 5ху. Цена единицы ресурса Х – 10 руб., единицы ресурса Y – 20 руб. Фирма располагает денежными средствами в размере 40 тыс. руб. Определите максимально возможный объем производства.

Задача 9.

Производственная функция фирмы имеет вид: Q (х, у) = (ХY)^1/2. Цена единицы ресурса Х – 4 руб., единицы ресурса Y – 5 руб. Определите, сколько единиц Х и Y должна ежедневно использовать фирма при общих затратах 150 тыс. руб. в день для максимизации выпуска.

Задача 10.

Технология производства фирмы описывается производственной функцией Q = К^0,5 L², где Q – объем выпускаемой за год продукции, К – объем основных фондов, L – объем использования рабочей силы. Определите предельный продукт труда, предельный продукт капитала и предельную норму технического замещения капитала трудом, если К = 9, L = 4.

Задача 11.

Когда фирма увеличивает применяемый капитал со 120 до 150 единиц, используемый труд с 500 до 625 единиц, выпуск продукции увеличивается с 200 до 220 единиц. Какой эффект роста масштаба производства имеет место в данном случае?

Задача 12.

Предположим, что когда фирма увеличивает применяемый капитал со 100 до 150 единиц, и используемый труд с 500 до 750 единиц, выпуск продукции увеличится с 200 до 280. Какой эффект масштаба производства имеет место в данном случае при увлечении использования каждого фактора?

Задача 13.

Определит тип эффекта масштаба, если на предприятии применяются два независимых производственных процесса. Один из них характеризуется производственной функцией Q^А =3К + Ц(0,5КL +L²), а другой – Q^В= 0,1К² + 0,2КL. Каким типом эффекта масштаба характеризуется каждый процесс?

Задача 14.

Фирма для производства 34 телевизоров использует следующее сочетание факторов: 1 ед. капитала и 3 ед. труда. В случае пропорционального удвоения всех факторов их комбинация будет выглядеть следующим образом 2 ед. капитала и 6 ед. труда. Такое сочетание факторов обеспечит объем производства, равный 71 телевизору. Определить эффект масштаба.

Задача 15.

Определить эффект масштаба при изменении количества затраченного труда для каждого объема производства.

Альтернативные способы производства продукции

Капитал, кол-во единиц (фактор К)	Труд, количество единиц (фактор L)
Капитал, кол-во единиц (фактор К)	1	2	3	4	5	6	7	8	9	10
1	4	11	34	47	55	54	52	49	45	39

Задача 16.

Определить эффект масштаба при изменении количества затраченного труда для каждого объема производства.

Альтернативные способы производства продукции (телевизоры, шт.)

Капитал, кол-во единиц (фактор К)	Труд, количество единиц (фактор L)
Капитал, кол-во единиц (фактор К)	1	2	3	4	5	6	7	8	9	10
1	61	71	81	90	98	106	110	113	115	116

Задача 17.

Технология производства описывается функцией Q = 5L ^0,5 * K. Чему будет равна предельная норма замещения капитала трудом при использовании 16 единиц капитала и 8 единиц труда?

Задача 18.

Производственная функция имеет вид: Q = 5L ^0,5 * K ^0,5. предположим, что в день затрачивается 4 часа труда и 4 часа работы машин. Определите:

1) максимальное количество выпускаемой продукции;

2) средний продукт труда;

3) допустим, что фирма увеличила затраты обоих факторов в два раза. Каков будет объем выпускаемой продукции?

Задача 19.

Производственная функция имеет вид: Q = 4L ^0,5 * 2K ^0,5. предположим, что в день затрачивается 9 часа труда и 9 часа работы машин. Определите средний продукт труда.

Задача 20.

Предположим, что производственная функция фирмы описывается уравнением Q = L ^0,25 * K ^0,75. На сколько процентов увеличится объем выпуска, если количество применяемого труда возрастет на 4%, а капитала - на 2%.

Задача 21.

Процесс производства на некотором предприятии описывается производственной функцией Q = 2L ^2/3 * K ^1/3. Найти алгебраическое выражение для изокванты при Q = 4.

Задача 22.

Предположим, что производственная функция фирмы описывается уравнением Q = L ^0,5 * K ^0,5. Во сколько раз увеличится выпуск продукции фирмой, если она в 4 раза увеличит использование обоих ресурсов?

Задача 23.

Предположим, что производственная функция фирмы описывается уравнением Q = L ^3/4 * K ^1/4. На сколько процентов увеличится объем выпуска, если количество применяемого труда возрастет на 8%, а капитала - на 4%.

Задача 24.

Известны производственная функция фирмы Q =2K^1/4L^3/4, стоимость единицы труда w = 15, стоимость единицы капитала r = 20 ден. ед, выпуск окончательного продукта в объеме 640 ед.

а) Требуется убедиться в том, что комбинация ресурсов L₁ = 16 ед., К₁= 256 *10⁴ ед., L₂=256 ед., K₂=625 ед., и L₃=4096 ед., K₃=625/4096 ед. обеспечивают заданный выпуск.

б) Найти стоимость заданного выпуска 640 ед. для каждой комбинации ресурсов и определить самый дешевый из них.

Задача 25.

Пусть производственная функция имеет вид Q = KL. Определить предельную норму замещения при Q = 10 для L = 1.

Задача 26.

Процесс производства на предприятии описывается производственной функцией Q = 2,5L^2/3K^1/3. Найдите алгебраическое выражение для изокванты, если Q = 5.

Задача 27.

Производственная функция фирмы имеет вид: Q = 7K^2/9 L^7/9. Цена капитала равна 4, цена труда равна 3. Фирма определила размер затрат в 24.

Найдите характер отдачи от масштаба производства и комбинацию факторов, при которой будет обеспечен максимальный выпуск.

Задача 28.

Производственная функция фирмы имеет вид: Q = AK L^β. Найдите предельную норму замещения К на L, если капиталовооруженность труда равна 10.

Задача 29.

Производственная функция имеет вид: Q = 2K^1/2 L^1/2, Р_L = 4, Р_к=3, Т_с = 24. Определите, какая комбинация факторов К и L обеспечивает максимальный выпуск.

Задача 30.

Технология производства описывается функцией Q = K^0,5 L. Чему будет равна предельная норма замещения капитала трудом при использовании 16 единиц капитала и 8 единиц труда?

Задача 31.

Производственная функция фирмы равна Q = K^{1/4 *}L^3/4. Цена капитала равна 4 тыс. руб. Цена труда равна 12 тыс руб. Какое количество капитала и труда должна иметь фирма для выпуска 300 тыс. единиц?

Задача 32.

Фирма платит 200 тыс. руб. в день за аренду оборудования и 100 тыс. руб. заработной платы. При этом она использует такое количество труда и капитала, что их предельные продукты соответственно равны 0,5 и 1

Использует ли фирма оптимальное сочетание факторов производства с точки зрения максимизации прибыли?

Задача 33.

Для производства 48 единиц продукта фирма использует 48 единиц труда и 12 единиц капитала. Какова будет предельная производительность капитала, если предельная производительность труда равна 0,5 и мы имеем постоянную экономию от масштаба?

Задача 34.

Производственная функция задана формулой Q = (KL)/2. Цена
единицы труда составляет 10 долл., цена единицы капитала — 5 долл.
Какова оптимальная комбинация ресурсов для производства товаров, в
количестве 10 единиц? Как изменятся минимальные издержки производства того же количества товаров, если цена единицы труда повысится до 20 долл.?

Тестовые задания

1. Определите, какая из перечисленных комбинаций значений общего продукта иллюстрирует закон убывающей предельной производительности фактора производства:

а) 2500, 1500, 12500, 1200;

б) 2500, 5000, 8000, 1200;

в) 2500, 3000, 3200, 3300;

г) 2500, 3500, 3600, 3800.

Вопросы для обсуждения

1. Какие факторы производства выделяют разные теории?

2. Обоснуйте основные свойства производственной функции.

3. Какая взаимосвязь существует между средним и предельным продуктами?

4. Какие виды отдач от масштаба выделяет экономическая теория?

5. Что представляет собой предельная норма технологического замещения?

7. Почему изокванты никогда не пересекаются?

Тема Издержки производства

Глоссарий

Издержки производства – это затраты на приобретение факторов производства

Бухгалтерские издержки (явные) - это произведенные в денежной форме фактические расходы, связанные с осуществлением производства

Экономические издержки (вмененные)– это альтернативная стоимость отвлекаемых для данного производства ресурсов

Бухгалтерская прибыль представляет собой общую выручку фирмы за вычетом внешних издержек

Экономическая прибыль – это общая выручка за вычетом всех издержек (внешних, внутренних)

Постоянные издержки (FC – fixed cost) – это издержки, величина которых не меняется в зависимости от изменения объема производства

Переменные издержки (VC – variable cost) – это издержки, величина которых меняется в зависимости от изменения объема выпуска продукции

Совокупные издержки – это сумма постоянных и переменных издержек

Средние постоянные издержки (AFC – average fixed cost) – это постоянные издержки, приходящиеся на единицу выпускаемой продукции

AFC = FC / Q

Средние переменные издержки (AVC – average variable cost) – это переменные издержки в расчете на единицу продукции

AVC = VC / Q

Предельные издержки (МС – marginal cost) – это дополнительные издержки, связанные с производством ещё одной дополнительной единицы продукции

МС= ∆ TC / ∆ Q

Долгосрочные средние издержки (LAC)– это долгосрочные издержки, приходящиеся на единицу выпускаемой продукции

LAC = LTC / Q

Долгосрочные предельные издержки - это дополнительные издержки, связанные с выпуском одной дополнительной единицы продукции в долгосрочном периоде

LMC =∆ LTC /∆ Q

Условие равновесия фирмы в краткосрочном периоде может быть сформулировано следующим образом:

МС=М R

Условие равновесия фирмы в долгосрочном периоде может быть сформулировано следующим образом:

МС=Р=АС= LAC

Задача 1.

Рассчитайте постоянные, переменные и предельные издержки.

Объем производства	Совокупные затраты
0	60
1	140
2	180
3	240
4	420

Задача 2.

Определить средние постоянные, средние переменные и предельные издержки.

Объем производства	Переменные затраты	Постоянные затраты
0	-	50
1	40	50
2	70	50
3	100	50
4	150	50
5	220	50

Задача 3.

Рассчитайте постоянные, переменные и предельные издержки.

Объем производства	Совокупные затраты
0	60
1	140
2	180
3	240
4	420

Задача 4.

Экономисты потеряли отчетность и вспомнили лишь несколько цифр, которые приведены в таблице. Досчитайте недостающие данные.

Q	TC	VC	AVC	AC	AFC	MC
0	100
10				20
20
30	390					11
40		420
50				14

Задача 5.

Функция средних переменных затрат имеет вид: АСV = 10 + 2Q . Постоянные затраты равны 12 ден. ед. Найти алгебраическое выражение для функции общих затрат.

Задача 6.

Функция общих затрат имеет вид: ТС = 30 + 5Q + Q². Определите выражения для постоянных, переменных, средних общих, средних постоянных, средних переменных и предельных затрат как функцию от Q.

Задача 7.

Функция общих затрат монополиста имеет вид ТС = 100 +3Q². Определите выражения для постоянных, переменных, средних общих, средних постоянных, средних переменных и предельных затрат как функцию от Q.

Задача 8.

Функция общих затрат имеет вид ТС = 100Q - 2Q² + 0,04Q³. Определить величину предельных затрат фирмы при Q= 12 единиц.

Задача 9.

Известно, что постоянные затраты фирмы равны 55 ден. ед. Функция предельных затрат фирмы имеет вид МС = 22 – 8Q + 3Q²+ 2Q³. Определить функцию общих затрат фирмы и рассчитать эти затраты при выпуске 3 единиц продукции.

Задача 10.

Известно, что постоянные затраты фирмы равны 80 ден. ед. Функция предельных затрат фирмы имеет вид МС = 30 – 10Q + 6Q²+ 1,6Q³. Определить функцию общих затрат фирмы и рассчитать эти затраты при выпуске 5 единиц продукции.

Задача 11.

Через год после начала деятельности бухгалтерская прибыль предприятия составила 400 тыс. ден. ед., чистая экономическая прибыль - 150 тыс. ден. ед. Определите явные и неявные издержки предприятия, если известно, что совокупный доход предприятия 900тыс. ден. ед.

Задача 12.

Хозяйка цветочного магазина наняла продавца с окладом 20 тыс. ден. ед. в год. Сумма ежегодной аренды - 8 тыс. ден. ед.она вложила в свое дело 40 тыс. ден. ед., лишившись 5 тыс. ден. ед. в год, которые она имела бы при другом помещении капитала. Свой предпринимательский талант она оценивает в 12 тыс. ден. ед. в год. Другая фирма предлагает ей работу с окладом 30 тыс. ден. ед. в год. Определите величину бухгалтерских и экономических издержек.

Задача 13.

Издержки одной типичной фирмы, работающей на конкурентном рынке, зависят от объема выпуска q как ТС = 5Q² + 2Q. Рыночная цена на продукцию фирмы 12 руб. Определите, будет ли фирма получать экономическую прибыль или нести убытки; какой уровень рыночной цены позволит фирме получать нормальную прибыль в долгосрочном периоде.

Задача 14.

Фирма, действующая на конкурентном рынке, имеет функцию средних переменных затрат AVC = 0,1g + 2. Постоянные затраты на производство составили 3. Найдите функцию предложения данной фирмы и отрасли в целом, если известно, что на рынке работает 100 подобных фирм.

Задача 15.

В конкурентной отрасли действует 100 одинаковых фирм. Общие издержки каждой фирмы составляют ТС (q) = 0,1 q² + 2 q + 50.

Определите уравнение кривой предложения отрасли и параметры краткосрочного равновесия на рынке, если спрос на товар в отрасли описывается уравнением Q_D = 5000 – 100Р. Проанализируйте перспективы развития отрасли в долгосрочном периоде.

Задача 16.

В краткосрочный период фирма производит 100 единиц товара при средних постоянных издержках 5 руб. Определить изменение общих издержек, если средние переменные издержки сократятся с 20 до 10 руб.

Тестовые задания

1. Из предложенного списка выберите функцию издержек, которая относится к долгосрочному периоду:

а) TC = 5Q² + 3Q + 10;

б) АC = 7Q + 10;

в) МC = 100Q + 5;

г) AVC = 5Q² + 75Q.

2. Функция совокупных издержек фирмы ТС = Q ³ – 10 Q ² + 28 Q . Следовательно:

а) фирма функционирует в краткосрочном периоде;

б) фирма функционирует в долгосрочном периоде;

в) невозможно определить, в каком периоде функционирует фирма;

г) издержки фирмы не могут принимать вид этой функции.

Неявные издержки - это

а) издержки бухгалтерские;

б) экономические издержки;

в) издержки упущенных возможностей;

г) альтернативные издержки использования ресурсов, являющихся собственностью фирмы.

На рисунке изображены кривые средних затрат фирмы в краткосрочном периоде. Если объем выпуска фирмы достиг такого значения, при котором средние постоянные затраты раны 4, то при этом величина предельных затрат попадает в интервал

а) МС<5;

б) 5<MC<9;

в) MC>9;

г) может быть все выше перечисленное.

На рисунке изображены кривые средних затрат фирмы в краткосрочном периоде. Если средние постоянные затраты равны 4 при таком объеме выпуска, при котором общие затраты равны 720, то общие переменные затраты при таком объеме выпуска равны

а) 80;

б) 320;

в) 360;

г) 400.

24. Если в краткосрочном периоде постоянные затраты равны 100 денежных единиц, а переменные затраты зависят от объема выпуска так VC ( q ) = 2 q , то при любом объеме выпуска краткосрочного периода:

а) предельные затраты будут меньше средних переменных;

б) предельные затраты будут меньше средних общих затрат;

в) предельные затраты будут больше средних общих затрат;

г) предельные затраты меньше средних постоянных затрат.

25. В краткосрочном периоде средние общие затраты фирмы при выпуске 20 – ти единиц меньше, чем средние общие затраты фирмы при выпуске 10 – ти единиц продукции. Следовательно, предельные затрат на выпуск 20-ой единицы продукции:

а) меньше предельных затрат на выпуск 20 - ой единицы продукции;

б) больше предельных затрат на выпуск 10 - ой единицы продукции;

в) равны предельным затратам на выпуск 10 - ой единицы продукции;

г) возможно все выше перечисленное.

Вопросы для обсуждения

1. Что такое издержки производства и какими двумя факторами они могут быть представлены?

2. Чем отличаются экономические издержки от бухгалтерских?

3. Что представляют собой постоянные издержки и чем они отличаются от переменных издержек?

4. Назовите факторы, определяющие конфигурацию кривых совокупных, средних и предельных издержек в краткосрочном и долгосрочном периодах.

5. Определите роль в исследовании издержек производства А. Смита, Д. Риккардо, К. Маркса, Менгера, Д. Кларка?

6. При каком объеме производства средние издержки достигают минимума?

7. Как рассчитывается бухгалтерская и экономическая прибыль?

8. Сформулируйте правило минимизации издержек.

9. Каковы пути снижения издержек фирмы?

Тема Рыночные структуры

Глоссарий

Рыночная структура – это совокупность признаков рыночной организации, определяющих характер взаимодействия фирм на отраслевом рынке и обуславливающих способ установления рыночного равновесия

Концентрация продавцов – это показатель удельного веса крупных производителей в отраслевом предложении

Коэффициент концентрации – процентное соотношение всех продаж, которое высчитывается для определенного числа фирм

Индекс Герфиндаля рассчитывается путем возведения в квадрат процентной доли рынка каждой из фирм и суммирования полученных результатов

К_г= d ₁ ² + d ₂ ² + d_n ²

n– число конкурирующих фирм;

d_n – доля рынка n-й фирмы в процентах

Совершенная конкуренция – тип рыночной структуры, где действует большое число небольших по размеру фирм, которые на способны оказывать влияние на цену и конкурируют между собой по цене

Чистая монополия – тип рыночной структуры, где единственный продавец противостоит множеству разнообразных покупателей

Двусторонняя монополия – тип рыночной структуры, где монополисту со стороны предложения противостоит монополист со стороны спроса

Монопсония – тип рыночной структуры, где множеству продавцов противостоит единственный покупатель, контролирующий у себя весь рыночный спрос

Монополистическая конкуренция – тип рыночной структуры, где обладающие рыночной властью продавцы дифференцированного продукта конкурируют за объем продаж

Олигополия – тип рыночной структуры, отличающийся стратегическим взаимодействием немногочисленных фирм, обладающих рыночной властью и конкурирующих за объем продаж

Дуополия – разновидность олигополии, где численность продавцов ограничена двумя фирмами

Олигопсония – тип рыночной структуры, где множеству продавцов противостоит ограниченное число покупателей, каждый из которых концентрирует у себя значительную часть рыночного спроса

Валовой доход определяется путем умножения цены на количество проданных единиц товара

TR = P * Q

Предельный доход – это увеличение валового дохода в результате увеличения выпуска продукции на одну единицу

MR = ∆ TR /∆ Q

Средний доход – это доход, получаемый от продажи одной единицы продукции

AR = TR / Q

Правило максимизации прибыли: прибыль максимальна, когда предельный доход фирмы равен предельным издержкам, т.е.

М R =МС

В условиях совершенной конкуренции прибыль максимальна, когда

М R =МС или МС = Р

Мертвый груз монополии – разница между потенциально возможным объемом производства в отрасли без монополии и реальным объемом выпуска монополиста

Для определения монопольной власти используется коэффициент Лернера:

L = (Р-МС)/Р

где: Р – цена;

МС – предельные издержки

L = -1/Е d

Равновесие Бертрана – описывает ситуацию на рынке, при которой в условиях дуополии фирмы конкурируют, понижая цену товара и увеличивая объем выпуска. Стабильность равновесия достигается тогда, когда цена оказывается равной предельным издержкам, т.е. достигается конкурентное равновесие

Равновесие Курно – достигается на рынке тогда, когда в условиях дуополии каждая фирма, действуя самостоятельно, выбирает такой оптимальный объем производства, какой ожидает от нее другая фирма. Равновесие Курно возникает как точка пересечения кривых реагирования двух фирм

Равновесие Штакельберга – описывает дуополию с неравным распределением рыночной власти между фирмами, так что одна из них ведет себя как лидер (либо по цене, либо в отношении объема, либо по тому и другому одновременно), в то время как другая осуществляет стратегию приспособления, корректируя свое поведение в зависимости от выбора, сделанного первой фирмой

Задача 1.

Фирма, находясь в условиях совершенной конкуренции, имеет следующую функцию общих затрат: ТС = 140 + 10Q + 40Q². При каком выпуске прибыль фирмы достигнет максимума, если цена установилась на уровне 250 ден. ед.? Определить размер прибыли фирмы.

Задача 2.

Фирма находится в условиях совершенной конкуренции. Функция ее общих затрат имеет вид ТС = 0,2Q² + 20Q + 10. Какой объем выберет фирма, если цена товара 60 ден. ед.? Какой должна быть цена, чтобы фирма прекратила производство в краткосрочном периоде?

Задача 3.

Ответьте на следующие вопросы, касающиеся совершенной конкурентной фирмы, используя диаграмму краткосрочных издержек:

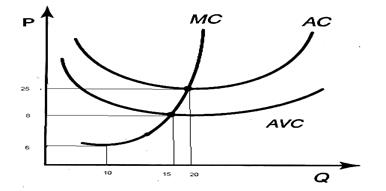
а) будет ли фирма в краткосрочном периоде производить продукцию при цене 6 руб. за единицу?

б) будет ли фирма производить продукцию при цене 10 руб. за единицу?

в) если цена 25 руб. за единицу, будет ли фирма получать экономическую прибыль?

Задача 4.

Определить точку “закрытия” фирмы в условиях совершенной конкуренции, если известно, что функция ее общих затрат имеет вид: TC = 40 + 2Q - 0,5Q² + 0,25Q³.

Задача 5.

Фирма находится в условиях совершенной конкуренции. Функция общих затрат имеет вид: TC = 0,1Q2 + 15Q +10. Какой объем производства выберет фирма, если цена товара 25 ден. ед.

Задача 6.

Продукт А на рынке совершенной конкуренции могут производить фирмы 2-х видов. Фирмы первого типа имеют общие затраты на уровне ТС₁ = 25Q-0,6Q² + 0,03Q³ TC₂ = 30Q – 0,04Q² +0,04Q³. И тех и других фирм может быть сколько угодно много. Сколько фирм каждого типа будет на рынке в долгосрочной перспективе, если спрос задан соотношением: Qd = 10260 – 20P?

Задача 7.

Функция общих издержек фирмы имеет вид: TC = 6Q + 2Q². Какую прибыль получит фирма, производящая и реализующая 25 единиц товара на рынке совершенной конкуренции по цене 36 ден. ед. за единицу товара?

Задача 8.

Фирма находится в условиях совершенной конкуренции. Зависимость общих затрат фирмы от выпуска продукции представлена в таблице.

Выпуск продукции, шт.	0	1	2	3	4	5	6
Общие затраты, ден. ед.	6	10	14	16	20	26	36

Ниже какого уровня должна опуститься цена, чтобы фирма прекратила производство продукции?

Задача 9.

Выпуск продукции, шт.	0	1	2	3	4	5
Общие затраты, ден. ед.	10	14	16	20	26	34

Если цена товара 7 ден. ед., какой объем производства следует выбрать?

Задача 10.

В совершенно конкурентной отрасли действуют 250 фирм, разбитых на три группы. Предельные издержки 100 фирм первой группы описываются уравнением МС_i = 100 Q_i + 1, 100 фирм второй - МС_i = 200 Q_i + 2, 50 фирм третьей - МС_i = 100 Q_i + 1. Функция спроса на рынке описывается уравнением Q = 25 – Р.

Задача 11.

В отрасли с совершенной конкуренцией функционирует 100 одинаковых фирм. Функция общих затрат каждой из них имеет вид TC = 2Q². Определите функцию предложения одной фирмы и всей отрасли. Определите равновесные значения цены и объема производства продукции, если функция спроса на продукцию отрасли имеет вид Q = 500 – 100P.

Задача 12.

Функция общих затрат монополиста имеет вид: ТС = 200 + 30Q, функция спроса на ее продукцию Р = 60 – 0,2Q. Определить цену, при которой фирма максимизирует прибыль.

Задача 13.

На монополизированном рынке функция спроса монополиста задается уравнением Q= 190 – Р, а функция предельных издержек монополиста: МС = 10 + 10Q. Средние издержки достигают минимального значения при объеме выпуска, равном 5 ед. Определить максимальную прибыль монополиста величину постоянных издержек.

Задача 14.

Функция затрат монополиста имеет вид TC = 5Q + 0,25Q². Монополия торгует на двух рынках, функция спроса на которых: Q₁ = 160- P₁; Q₂ = 160 – 2P₂. Определить цены на каждом рынке, при которых прибыль монополиста будет максимальной.

Задача 15.

Определить выпуск, максимизирующий прибыль монополиста, цену и размер прибыли, если функция спроса на продукцию монополиста Q = 12 – Р, а функция общих затрат ТС = 2 + 6Q + Q².

Задача 16.

Информация о функции спроса на продукцию монополиста и его общих затратах приведена в таблице.

Выпуск в единицу времени	Цена, ден. ед.	Общие затраты, ден. ед.
1	12	29
2	11	31
3	10	32
4	9	34
5	8	37
6	7	42
7	6	49
8	3	59

При каком выпуске монополист максимизирует прибыль и какую цену при этом назначит?

Задача 17.

В таблице показана цена спроса, с которой сталкивается монополист:

Цена	9	8	7	6	5	4	3	2	1	0
Спрос	0	1	2	3	4	5	6	7	8	9

а) рассчитать предельный доход монополиста;

б) какова величина выпуска, максимизирующего прибыль монополиста, если предельные издержки постоянны и равны 5 ден. ед.?

Задача 18.

Фирма выпускает товар в условиях монополии. Функция спроса на данный товар Р = 144 – 3Q, а функция средних издержек АС = 25/Q + Q.

Задача 19.

В таблице показана цена спроса, с которой сталкивается фирма в условиях монополистической конкуренции:

Цена	9	8	7	6	5	4	3	2	1
Объем спроса	1	2	3	4	5	6	7	8	9

а) рассчитать предельный доход фирмы в условиях монополистической конкуренции;

б) какова величина выпуска, максимизирующего прибыль монополиста, если предельные издержки постоянны и равны 6 ден. ед.?

Задача 20.

Определить монополистическую власть для каждой фирмы.

Фирма	Цена	Предельные издержки
А	250	271
В	375	314
D	198	200
C	212	215

Задача 21.

Определить монополистическую власть для каждой фирмы

Фирма	Р₁	Р₂	Q₁	Q₂
А	20	24	18	16
В	37	41	21	18
D	45	50	27	25
C	54	62	32	29
Е	17	25	37	34

Задача 22.

Цена товара составляет 50 долларов, предельные издержки его производства 45 долларов. Фирма контролирует 27% отраслевого объёма продаж. Другие крупные фирмы в этой отрасли реализуют в этой отрасли соответственно 10% ,7% и 6 % рынка определите индекс Лернера, рассчитайте индекс Герфиндаля, определите относится ли отрасль к числу высоко концентрированных отраслей экономики США.

Задача 23.

На рынке действует 7 фирм, контролирующих соответственно 5, 20, 5, 20, 25, 10 и 15% отраслевого объема выпуска. Будут ли разрешены слияния 1-й и 6-й фирм? 2-й и 5-й? Сделайте анализ отраслевого рынка.

Задача 24.

В отрасли действует 4 фирмы, доля каждой соответсвенно составляет 20%, 15%, 30% и 35. Определить индекс Герфиндаля.

Задача 25.

Фирма монополизировала производство кресел для офисов. Определить цену и объем выпуска данных товаров, если имеются следующие данные о положении фирмы: MR=2000 - 40Q , TR=2000Q-20Q², MC=200+20Q, где Q- объем производства. Как изменится цена и объем выпуска, если эта фирма будет работать в условиях совершенной конкуренции?

Задача 26.

Пусть функция издержек фирмы-монополиста равна ТС(Q) = Q² + 60. Функция спроса на товар фирмы: Q_D = 30 – 2Р. Определите объем производства, цену, общую выручку, экономическую прибыль монополиста и его монопольную власть.

Задача 27.

Компания «Джеральдс» - монополист на рынке. Функция полных затрат на производство: ТС = 2Q + 10. Определите, при каком уровне цены прибыль компании будет максимальной, если известно, что эластичность рыночного спроса в этой точке по цене равна – 6.

Задача 28.

Функция полных затрат фирмы-монополиста: ТС = Q² + 2Q. Функция рыночного спроса на ее продукцию: Р = 20 – Q. Государство вводит потоварный налог (на каждую единицу продукции) в количестве 2 ден. ед. Определите налоговые поступления в бюджет, выпуск и цену, максимизирующие прибыль монополиста, после введения налога.

Задача 29.

Издержки фирмы-монополиста описываются формулой: ТС = 5Q + 12. Функция рыночного спроса на ее продукцию: Р = 120 – 0,5 Q. Государство вводит потоварный налог (на каждую единицу продукции) в количестве 2 ден. ед. Определите поступления в бюджет; максимизирующие прибыль монополии выпуск и цену на продукцию после введения налога.

Задача 30.

Функция общих издержек монополиста имеет вид ТС = 100 + 3Q, функция спроса на его продукцию имеет вид Р = 200 – Q. Определите доход монополиста, если монополист выпускает 20 ед. продукта в месяц.

Задача 31.

На рынке чистой монополии объем производства составляет 5 ед., монопольная цена равна 5 тыс. ден. ед., а средние валовые издержки – 2 тыс. ден. ед. Определите экономическую прибыль (убыток) монополии.

Задача 32.

Функция спроса на продукцию монополиста описывается уравнением P = 30 – 0,5Q, а функция общих затрат TC = 2Q = 0,5Q². Определите при какой цене и каком объеме он получит максимальную прибыль.

Тестовые задания

1. Монополист выпускает и продает такой объем продукции, при котором, чтобы получить максимум прибыли при переходе к условиям совершенной конкуренции, фирма должна:

а) повысить цену и увеличить объем выпуска;

б) снизить цену и уменьшить объем выпуска;

в) повысить цену и сохранить прежний объем выпуска;

г) снизить цену и увеличить объем выпуска.

2. Если кривая спроса линейна, а предельные издержки равны средним и постоянным, то объем выпуска монополии:

а) в два раза больше, чем в конкурентной отрасли;

б) равен выпуску конкурентной отрасли;

в) в два раза меньше, чем в конкурентной отрасли;

г) данных недостаточно.

3. В городе открылся первый ночной магазин. Это пример скорее всего:

а) естественной монополии;

б) вынужденной монополии;

в) временной монополии;

г) монопсонии.

4. Антимонополистическое законодательство, действующее во многих странах, нацелено в первую очередь на обеспечение:

а) запрета монополий;

б) экономической свободы;

в) условий конкуренции;

г) регулирования цен.

5. Выберите из нижеперечисленного условие долгосрочного равновесия фирмы – участника рынка, характеризующегося монополистической конкуренцией:

а) Р = АС;

б) Р = МС = АС;

в) Р = МР;

г) Р = АVС.

6. Характерными чертами монополистической конкуренции являются:

а) отсутствие зависимости прибыли участников от управленческих решений одной из фирм;

б) дифференциация выпускаемого продукта;

в) кривая спроса менее эластична, чем кривая спроса на продукт конкурирующего производителя;

г) верно все перечисленное.

7. На рынке монополистической конкуренции:

а) отдельный покупатель может влиять на цену продукции;

б) реклама не играет существенной роли;

в) товары отличаются по исполнению и условиям продажи;

г) производители имеют одинаковый доступ к информации.

Конкуренция способствует

а) улучшению экологической ситуации в результате конкурентной борьбы;

б) поддержанию благосостояния всех граждан на высоком уровне;

в) производству необходимых обществу товаров, эффективному использованию ресурсов;

г) равномерному распределению доходов в обществе.

Вопросы для обсуждения

1. Что такое рыночная структура? Назовите ее основные признаки.

2. Какие коэффициенты используются для измерения концентрации рынка?

3. Что такое монополистическая конкуренция и каковы ее основные черты?

4. Как определяется оптимальный объем производства в условиях совершенной конкуренции?

5. Что такое монополия? Какие виды монополии различаются в экономической теории?

6. Что такое олигополия и каковы ее основные характеристики?

7. Назовите основные источники монопольной власти.

Тема Рынки факторов

Глоссарий

Предельная доходность ресурса рассчитывается по формуле:

MRP = MP * MR

где: MRP – предельная доходность ресурса;

MP – предельный продукт данного ресурса

MR – предельный доход фирмы

Для фирмы совершенного конкурента предельная доходность ресурса равна стоимости предельного продукта:

MRP =МР*Р

Правило максимизации прибыли: фирма, максимизирующая прибыль должна использовать такое количество переменного фактора, при котором его предельный продукт в денежной форме будет равен его предельным издержкам

MRP_L = MRC_L

Задача 1.

На рынке труда спрос на труд описывается уравнением DL = 100 – 2W, а предложение труда описывается уравнением SL = 40 + 4 W, где W – дневная ставка заработной платы в долларах. Определить какая ставка заработной платы установится на этом рынке, и какое количество работников будет нанято на работу.

Задача 2.

В удаленном от районного центра поселке лесхоз является единственным предприятием. Функция спроса лесхоза на труд выражена как DL = 102 – 2W, а функция предложения труда SL = 6 + W, где W – дневная ставка заработной платы в долларах. Каким будет уровень оплаты труда и занятость в данном случае.

Задача 3.

Фирма продает продукцию на конкурентном рынке, условия спроса на котором задаются уравнением Q_D = 25 – Р, а предложения : Q_s = Р – 5, где Р – рыночная цена; Q – объем сделок в натуральном выражении. Производственная функция данной фирмы задается уравнением: Q(L,К) = 30L - 2L² + 4К, где Q – общий выпуск фирмы; L и К – количества используемых труда и капитала. Выведите уравнение спроса фирмы на труд, если рынок труда конкурентный.

Задача 4.

Функция полезности работника имеет вид: U = C^0,5 L^0,5, где С - количество потребительских благ; L – свободное время. Ставка заработной платы в номинальном выражении равна 20 руб./ч. Величина дохода помимо заработной платы составляет 80 руб./день. Уровень цен на потребительские блага равен 2. Определите объем предложения труда работником в день.

Задача 5.

Условия спроса на конкурентном рынке труда характеризуются уравнением: ωd = 10 – 1/5L, а предложения: ω_s= 2 + 1/450L², где ω_s – почасовая ставка заработной платы; L – количество человеко-часов за данный промежуток времени. Найдите экономическую ренту работников.

Задача 6.

В краткосрочном периоде производственная функция фирмы: Q (L_i) = 16L_i - L_i², где L_i – объем труда, используемого данной фирмой, 0 ≤ L_i ≥ 6. В отрасли действует 10 идентичных конкурентных фирм. Отраслевой спрос на выпускаемую продукцию задан функцией: Р = 10 – Q, где Q - отраслевой объем производства. Труд продается и покупается на конкурентном рынке. Выведите обратную функцию отраслевого спроса на труд.

Задача 7.

В краткосрочном периоде производственная функция фирмы: Q (L_i) = L_i^0,5 , где L_i – объем труда, используемого данной фирмой. В отрасли действует n идентичных конкурентных фирм. Отраслевой спрос на выпускаемую продукцию задан функцией Q = 1/Р, где Q – отраслевой объем производства. Труд продается и покупается на конкурентном рынке. Выведите обратную функцию отраслевого спроса на труд.

Задача 8.

Единственным работодателем на рынке труда является фирма - совершенный конкурент на рынке продукта (цена продукта равна 2 у.е.), производственная функция которой имеет вид: Q = 50L – 0,25L² (0 ≤ L≤ 100). Фирма практикует дискриминацию по половому признаку при найме на работу. Предложение труда мужчин описывается функцией: L_s = -20 + 2W, а женщин - L_s = 10 + 0,5W.

Определите:

1) сколько женщин и мужчин будет принято на работу; какова будет ставка зарплаты для мужчин и для женщин;

2) какова была бы ставка зарплаты и сколько женщин и мужчин было бы нанято, если бы фирма не могла применять дискриминацию рабочей силы по половому признаку.

Задача 9.

В таблице представлена ставка заработной платы за единицу труда.

Единица труда	Ставка заработной платы	Совокупные издержки на оплату труда	Предельные издержки на ресурс
0	10
1	15
2	20
3	25
4	30
5	35
6	40

Задача 10.

Для производства товара использовался ресурс А. Определить его предельный доход.

Единица ресурса	Продукт, всего	Предельный продукт	Цена продукта	Общий доход	Предельный доход
0	-		5
1	10		5
2	18		5
3	24		5
4	28		5
5	30		5
6	31		5

Задача 11.

Для производства товара использовался ресурс А. Определить его предельный доход.

Единица ресурса	Продукт, всего	Предельный продукт	Цена продукта	Общий доход	Предельный доход
0	-		6
1	15		5
2	18		4,5
3	25		4
4	27		3,5
5	30		3
6	33		2,5

Задача 12.

В таблице представлена ставка заработной платы за единицу труда. Определить предельные издержки на ресурс.

Единица труда	Ставка заработной платы	Совокупные издержки на оплату труда	Предельные издержки на ресурс
2	10
6	10
9	10
11	10
15	10
17	10
20	10

Задача 13.

Спрос на землю описывается уравнением Q = 100- 2R, где Q – площадь земельных угодий, R – земельная рента. Если площадь земельных угодий равна 90 га, а ставка ссудного процента 12% годовых, определить цену 1 га земли.

Задача 14.

Фермер – арендатор получает 20% прибыли на 50 тыс. долл. капитала вложенного в землю. Величина прибавочного продукта, получаемого после реализации продукции, составляет 30тыс. долл. определите величину ренты, получаемой собственником земли.

Задача 15.

В двух хозяйствах под рожь занято по 1 тыс. га, разных по плодородию. Урожайность соответственно составила 30 и 40 ц с 1 га. Если цена за 1 ц установлена на уровне индивидуальной стоимости первого хозяйства и равна 500 руб., какова будет дифференциальная рента в обоих хозяйствах. индивидуальная стоимость 1 ц во втором хозяйстве – 300 руб.

Задача 16.

В земельный участок вложен капитал 100 тыс. долл., срок окупаемости затрат – 20 лет. Рента с этого участка составляет 25 тыс. долл. Если норма ссудного процента установлена в размере 5%, определите сумму арендной платы.

Задача 17.

Даны два одинаковых по площади участка земли, в которые вложено по 1000 долл. урожайность составила 20 и 30 ц зерна. Если абсолютная земельная рента за каждый участок равна 500 долл., определите цену каждого участка при условии, что средняя норма прибыли – 20%, а норма ссудного процента – 10%.

Задача 18.

Какова будет цена земельного участка, если землевладелец ежегодно получает 60 тыс. ден. ед. земельной ренты, а банк выплачивает вкладчикам 10% годовых?

Задача 19.

Собственник земли получает ежегодно арендную плату за сданный в аренду участок 8 тыс. ден. ед. На участке имеются сельскохозяйственные постройки и сооружения стоимостью 50 тыс. ден. ед. со сроком службы 10 лет. Норма банковского процента 5% годовых. Определите величину земельной ренты.

Задача 20.

Ферма А произведет 3700 ц ржи средние издержки 10 долл. за 1 ц. Цена равны 5 долл. за 1 ц. Ферма В произведет 3700 ц средние издержки 6 долл. за 1 ц., а цена равна 7 долл. за 1 ц. Ферма С произведет 2500 ц средние издержки 10 долл. за 1 ц., а цена равна 15 долл. за 1 ц. Определить дифференциальную земельную ренту для каждой фермы.

Задача 21.

Функция спроса на землю задается как Q_D= 8800-20R, где Q_D – площадь земли, а R – земельная рента в тыс. руб. Площадь, предполагаемая для продажи земли составляет 1200 га, а ставка ссудного процента 8%. Определить цену земли.

Задача 22.

Если участок земли площадью 10 га продается по цене 8 тыс.руб. за один га, а годовая процентная ставка составляет 5%, то участок приносит в течение года ренту, равную _____ тыс. руб.

Задача 23.

Определите величину экономической ренты по каждому из 3-х графиков

Задача 24.

Предложение земли описывается уравнением Q = 10 га. Спрос фермеров на землю описывается уравнением Q = 50 – Р. В результате роста спроса на продукты питания увеличило спрос на землю до Q = 100 – Р. Определите, насколько возросла земельная рента, если ставка банковского процента уменьшилась с 10% годовых до 5% годовых, а плата за вложенный капитал и отчисления на амортизацию не изменились.

Задача 25.

В результате осушения болота площадь земель, пригодных для строительства жилых домов, увеличилась в два раза. Строительная компания покупает землю под застройку жилых домов и сдачи квартир внаем. Спрос строительной компании на землю описывается уравнением Q = 100 – Р. Предложение земли абсолютно неэластично. Строительная компания получает нулевую экономическую прибыль. Определите, при каких условиях арендная плата для квартиросъемщиков увеличится и будет ли доход, получаемый строительной компанией от сдачи построенного жилья внаем, земельной рентой.

Задача 26

Владелец первого участка земли согласен продать его за 20 000 руб. Владелец другого участка земли согласен продать его за 10 000 руб. Определите, чему равна ежегодная дифференциальная рента, если ставка банковского процента равна 10%, а плата за вложенный капитал и отчисления на амортизацию на обоих участках земли одинаковые.

Задача 27.

Предложение земли описывается уравнением Q = 100. Спрос железнодорожной компании на землю описывается уравнением Q = 200 – Р, а спрос фермера на землю - Q = 150 – Р.

Определите:

1) цену земли, если собственник решит продать участок ;

2) ежегодную плату при сдаче земли в аренду, если ставка банковского процента равна 5% годовых;

3) земельную ренту, если ежегодная амортизация равна 0,5 тыс. руб., а вложенный капитал – 10 тыс. руб.

Задача 28.

Земельный участок приносит ежегодный доход 100000 руб. Годовая ставка банковского процента 10%. Определить цену этого участка как бессрочного (вечного) капитального актива.

Задача 29.

Площадь доступных земельных угодий составляет 1200 га. Спрос на землю описывается уравнением Q = 180 – 3R. Ставка банковского процента равна 10%. Определить, чему равна равновесная ставка ренты.

Тестовые задания

Вопросы для обсуждения

1. Чем определяется цена земли?

2. Какие основные формы может принимать капитал?

3. Как образуется земельная рента?

4. В чем состоит сущность дифференциальной ренты?

5. Какую роль играют эффекты дохода и замещения отдыха трудом при решении человека о количестве предлагаемого труда?

6. В чем заключается эффект Фишера?

7. В чем отличие рынков факторов производства от рынков товаров и услуг?

РАЗДЕЛ I . ВВЕДЕНИЕ В ЭКОНОМИЧЕСКУЮ ТЕОРИЮ

Дата: 2018-12-21, просмотров: 654.

12 3 4 5 6 7 8 9 10 Следующая ⇒