Линейная алгебра и аналитическая геометрия.
Решение вырожденных систем линейных уравнений.
Если определитель матрицы 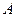 системы линейных уравнений равен нулю (или число уравнений системы меньше числа неизвестных), то либо имеется бесконечно много решений, либо система противоречива, и решений нет вовсе. Разберем на примере, как можно описать все решения вырожденной системы уравнений, используя метод Гаусса последовательного исключения неизвестных.
системы линейных уравнений равен нулю (или число уравнений системы меньше числа неизвестных), то либо имеется бесконечно много решений, либо система противоречива, и решений нет вовсе. Разберем на примере, как можно описать все решения вырожденной системы уравнений, используя метод Гаусса последовательного исключения неизвестных.
Задача 1.2. Решить систему уравнений
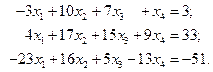
Решение. С помощью первого уравнения исключим переменную 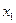 из второго и третьего уравнений системы.
из второго и третьего уравнений системы.
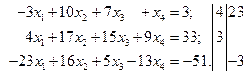
Получаем:
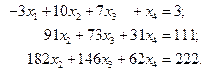
Исключим теперь с помощью второго уравнения системы переменную 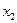 из третьего уравнения.
из третьего уравнения.
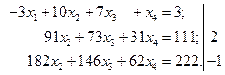
В результате третье уравнение системы превращается в тождество 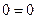 , и остается только два уравнения:
, и остается только два уравнения:
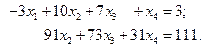
Мы привели систему к верхнетреугольному виду, однако для двух неизвестных (а именно, для 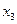 и для
и для 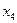 ) не хватило “своего” уравнения для преобразования исключения. В этом случае переменные
) не хватило “своего” уравнения для преобразования исключения. В этом случае переменные 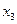 ,
, 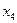 объявляются свободными (то есть их значения могут выбираться произвольным образом), а значения остальных переменных (они называются базисными) могут быть выражены через значения свободных переменных.
объявляются свободными (то есть их значения могут выбираться произвольным образом), а значения остальных переменных (они называются базисными) могут быть выражены через значения свободных переменных.
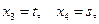
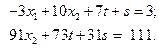
Отсюда:
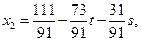
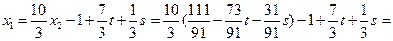
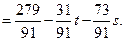
Ответ: 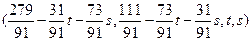 , где
, где 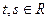 - произвольные параметры.
- произвольные параметры.
Геометрия на плоскости.
Каноническое уравнение прямой на плоскости имеет вид
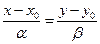 ,
,
где 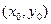 ¾ произвольная точка на прямой, а
¾ произвольная точка на прямой, а 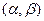 – направляющий вектор. Если уравнение прямой записано в виде
– направляющий вектор. Если уравнение прямой записано в виде
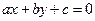 ,
,
то 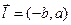 – направляющий вектор, а
– направляющий вектор, а 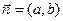 - вектор нормали (направленный по перпендикуляру к прямой). Нам потребуется еще формула деления отрезка пополам: если задан отрезок
- вектор нормали (направленный по перпендикуляру к прямой). Нам потребуется еще формула деления отрезка пополам: если задан отрезок 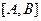 , и координаты точек
, и координаты точек 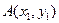 ,
, 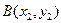 известны, то серединой отрезка
известны, то серединой отрезка  является точка
является точка
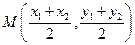 .
.
Задача 1.3. В треугольнике ABC с вершиной A(10,7) известны уравнения высоты BB1:
2x-y+37=0
и медианы CC1:
8x+11y-162=0.
Написать уравнения всех сторон треугольника ABC.
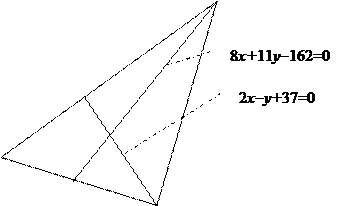 C
C
B1
A(10,7)
C1 B
Решение. Проще всего написать уравнение стороны 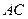 , поскольку мы знаем точку
, поскольку мы знаем точку 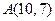 , через которую проходит прямая
, через которую проходит прямая 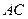 , и знаем направляющий вектор
, и знаем направляющий вектор 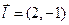 (вектор нормали к высоте
(вектор нормали к высоте 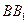 ). Следовательно, уравнение
). Следовательно, уравнение 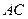 имеет вид
имеет вид
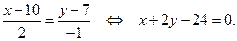
Чтобы написать уравнение прямой 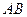 , найдем сначала координаты точки
, найдем сначала координаты точки 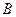 . Обозначим эти координаты через
. Обозначим эти координаты через 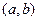 . С одной стороны, точка лежит
. С одной стороны, точка лежит 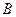 на прямой
на прямой 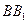 , и, следовательно,
, и, следовательно,
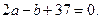
С другой стороны, поскольку 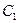 является серединой отрезка
является серединой отрезка 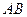 , то
, то 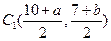 . Но
. Но 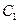 лежит на прямой
лежит на прямой 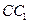 , поэтому
, поэтому
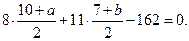
Решая совместно систему уравнений
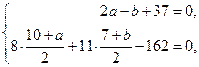
получаем

Итак, точка 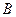 имеет координаты
имеет координаты 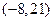 , направляющий вектор прямой
, направляющий вектор прямой 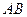 равен
равен 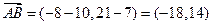 . Уравнение прямой
. Уравнение прямой 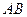 имеет вид
имеет вид
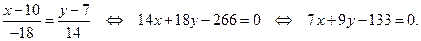 Прежде чем написать уравнение прямой
Прежде чем написать уравнение прямой 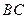 , найдем координаты точки
, найдем координаты точки 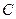 . Она лежит на пересечении прямых
. Она лежит на пересечении прямых 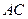 и
и 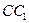 , поэтому ее координаты являются решением системы уравнений
, поэтому ее координаты являются решением системы уравнений
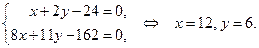
За направляющий вектор прямой 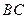 можно взять вектор
можно взять вектор
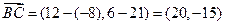 ,
,
а уравнение 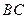 запишется в виде
запишется в виде
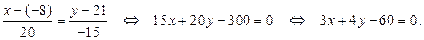 Аналитическая геометрия в пространстве.
Аналитическая геометрия в пространстве.
Нам необходимо знать следующие три операции над векторами в трехмерном пространстве.
1) Скалярное произведение векторов:
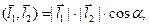
где  ,
, 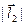 – длины векторов
– длины векторов 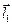 и
и 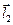 , а
, а 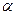 - угол между ними. В координатах: если
- угол между ними. В координатах: если 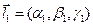 ,
, 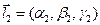 , то
, то
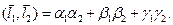
2) Векторное произведение векторов: 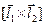 есть вектор,
есть вектор,
а) направленный по нормали к плоскости, натянутой на вектора 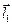 ,
, 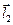 ;
;
б) имеющий длину, равную площади параллелограмма  , построенного на векторах
, построенного на векторах 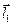 ,
, 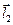 ;
;
в) и, наконец, направление вектора 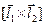 должно быть таким, что вращение от вектора
должно быть таким, что вращение от вектора 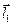 к вектору
к вектору 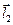 внутри параллелограмма
внутри параллелограмма 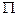 будет осуществляться против часовой стрелки, если глядеть с конца стрелки вектора
будет осуществляться против часовой стрелки, если глядеть с конца стрелки вектора 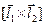 .
.
В координатах:
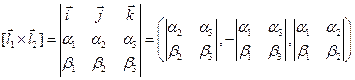 .
.
3) Смешанное произведение векторов:
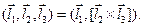
В координатах:
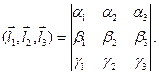
Геометрический смысл смешанного произведения векторов состоит в том, что 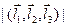 есть объем параллелепипеда, построенного на векторах
есть объем параллелепипеда, построенного на векторах 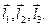
Каноническое уравнение прямой в пространстве имеет вид:
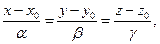
где 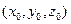 - координаты произвольной точки прямой, а
- координаты произвольной точки прямой, а 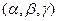 есть произвольный направляющий вектор.
есть произвольный направляющий вектор.
Имеется два типа уравнения плоскости в пространстве
а) 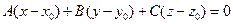 .
.
Здесь 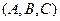 - вектор нормали к плоскости, а
- вектор нормали к плоскости, а 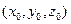 - координаты произвольной точки плоскости.
- координаты произвольной точки плоскости.
б) 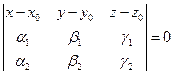 ,
,
где 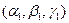 ,
, 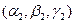 - любые два неколлинеарных вектора, параллельных плоскости, а
- любые два неколлинеарных вектора, параллельных плоскости, а 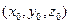 , по-прежнему, произвольная точка плоскости.
, по-прежнему, произвольная точка плоскости.
Задача 1.4. В пирамиде ABCD с вершинами A(10,7,1), B(7,10,0), C(1,10,7), D(7,1,17) найти:
а) угол между ребрами AB и AD;
б) угол между ребром AD и плоскостью ABC;
в) площадь основания ABC;
г) объем пирамиды;
д) расстояние от вершины D до плоскости ABC.
Написать уравнение высоты, опущенной из вершины D на плоскость ABC, и уравнение плоскости ABC.
Решение. а). Найдем векторы 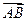 и
и 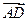 в координатах. Напомним, что для этого следует из координат конца вектора вычесть координаты начала:
в координатах. Напомним, что для этого следует из координат конца вектора вычесть координаты начала:
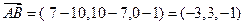 ,
,
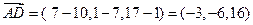 .
.
Чтобы найти угол между векторами 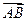 ,
, 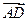 , вычислим скалярное произведение векторов
, вычислим скалярное произведение векторов 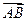 и
и 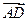 в координатах, затем найдем длины векторов
в координатах, затем найдем длины векторов 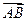 и
и 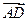 , и подставим полученные значения в формулу скалярного произведения. Получаем:
, и подставим полученные значения в формулу скалярного произведения. Получаем:
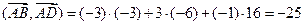 ,
,
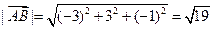 ,
,
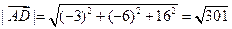 .
.
Подставляем в формулу скалярного произведения:
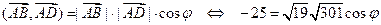 ,
,
откуда 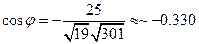 ,
, 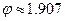 .
.
б) Угол между ребром AD и плоскостью ABC равен 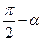 , где
, где 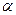 - угол между ребром AD и нормалью к плоскости ABC. Начнем поэтому с вычисления нормали к плоскости ABC. В качестве вектора нормали можно взять векторное произведение векторов
- угол между ребром AD и нормалью к плоскости ABC. Начнем поэтому с вычисления нормали к плоскости ABC. В качестве вектора нормали можно взять векторное произведение векторов 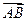 и
и 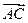 (поскольку
(поскольку 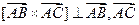 ). Вектор
). Вектор 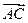 в координатах имеет вид
в координатах имеет вид
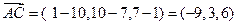 .
.
Следовательно,
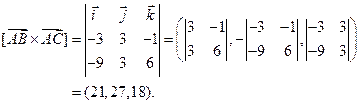
Обозначим для краткости 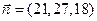 . Теперь, как и в пункте а) вычислим скалярное произведение векторов
. Теперь, как и в пункте а) вычислим скалярное произведение векторов 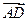 и
и  , и с его помощью определим угол между векторами
, и с его помощью определим угол между векторами 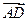 и
и 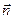 .
.
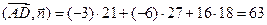 ,
,
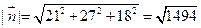 ,
,
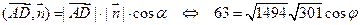 ,
,
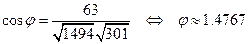 .
.
Следовательно, угол между ребром AD и плоскостью ABC равен 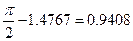 .
.
в) Площадь основания ABC равна половине площади параллелограмма, построенного на векторах 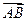 и
и 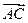 . По второму свойству векторного произведения, длина вектора
. По второму свойству векторного произведения, длина вектора 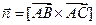 как раз и равна площади этого параллелограмма. Следовательно,
как раз и равна площади этого параллелограмма. Следовательно,
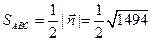 .
.
г) Объем пирамиды равен одной шестой от объема параллелепипеда, построенного на векторах 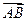 ,
, 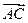 ,
, 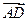 . Объем параллелепипеда можно вычислить как модуль смешанного произведения
. Объем параллелепипеда можно вычислить как модуль смешанного произведения 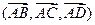 . Имеем:
. Имеем:
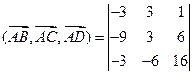 .
.
Заметим, однако, что нам нет необходимости заново вычислять этот определитель, поскольку он равен скалярному произведению векторов 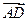 и
и 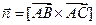 , а эта величина была найдена выше, в пункте б). Следовательно,
, а эта величина была найдена выше, в пункте б). Следовательно,
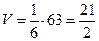 .
.
д) Расстояние от вершины D до плоскости ABС можно найти, используя формулу объема пирамиды
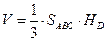 ,
,
поскольку все величины в ней, кроме высоты 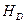 (которая и равна расстоянию от точки D до плоскости ABС), уже известны. Получаем:
(которая и равна расстоянию от точки D до плоскости ABС), уже известны. Получаем:
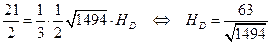 .
.
В заключение, напишем уравнение высоты, опущенной из вершины D на плоскость ABC, и уравнение плоскости ABC.
Направляющий вектор высоты 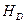 равен
равен 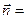 (21,27, 18). Высота
(21,27, 18). Высота 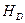 проходит через точку D(7, -1,17). Следовательно, каноническое уравнение высоты имеет вид
проходит через точку D(7, -1,17). Следовательно, каноническое уравнение высоты имеет вид
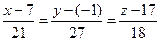 .
.
Чтобы написать уравнение плоскости 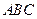 , воспользуемся уравнением
, воспользуемся уравнением 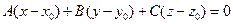 . В качестве вектора
. В качестве вектора 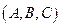 вновь можно использовать вектор нормали
вновь можно использовать вектор нормали 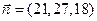 , а в качестве
, а в качестве  – точку A(10,7,1). Получаем:
– точку A(10,7,1). Получаем:
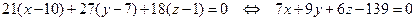 Задача полностью решена.
Задача полностью решена.
Математический анализ
Предел и производная.
Производные.
Производной функции 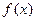 в точке
в точке 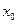 называется предел
называется предел
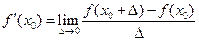 .
.
Наряду с обозначением 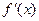 для производной используется еще обозначение
для производной используется еще обозначение 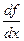 .
.
Производные основных элементарных функций приведены в следующей таблице.
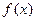
| 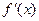
|
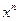
| 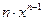
|
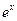
| 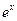
|
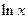
| 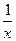
|
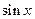
| 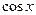
|
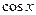
| 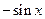
|
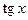
| 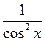
|
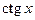
| 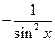
|
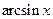
| 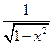
|
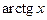
| 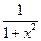
|
Рассмотрим дифференцирование степенной функции при некоторых 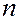 .
. 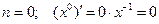
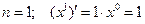
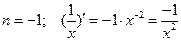
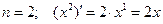
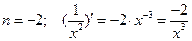
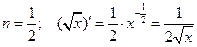
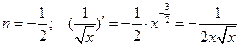
Имеется два основных приема дифференцирования функций
1) Формула дифференцирования произведения и частного двух функций
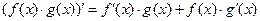 ,
,
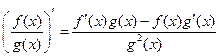 .
.
2) Формула дифференцирования композиции (или сложной функции)
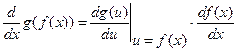 .
.
Примеры дифференцирования сложной функции .
1°) 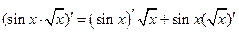
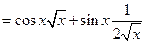
2°) 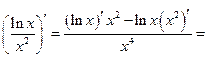
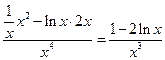
3°) 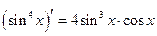
4°) 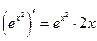
5°) 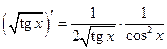
6°) 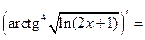
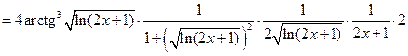
В задачах 2.2.а - 2.2.з для функции 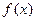 требуется найти производную
требуется найти производную 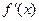 .
.
Задача 2.2.а 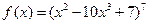 .
.
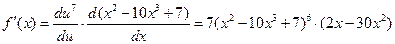 .
.
Задача 2.2.б 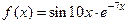 .
.
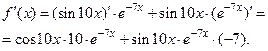
Задача 2.2.в 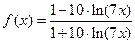 .
.
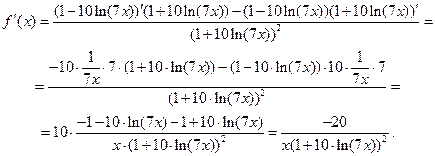 Задача 2.2.г
Задача 2.2.г 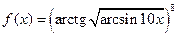 .
.
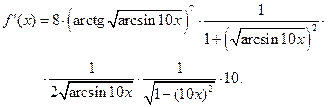
Задача 2.2.д 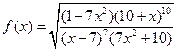 .
.
Решение. При дифференцировании этой функции удобно воспользоваться приемом, который называется логарифмическим дифференцированием. Прежде чем вычислять производную, найдем логарифм функции 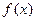 :
:
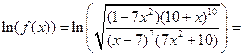
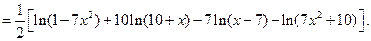
Теперь продифференцируем правую и левую часть полученной формулы, а затем приравняем соответствующие производные. Имеем:
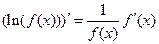 ;
;
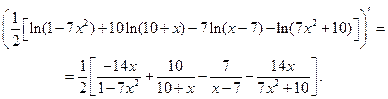
Отсюда,
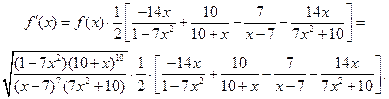
Задача 2.2.е 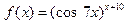 .
.
Решение. Здесь также удобно воспользоваться приемом логарифмического дифференцирования.
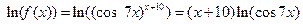 ;
;
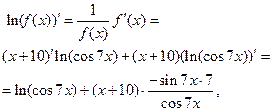
откуда следует, что
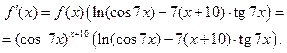
Задача 2.2.ж 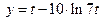 ,
, 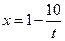 .
.
Решение. Функция 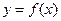 задана в параметрической форме, поэтому следует воспользоваться формулой для параметрической производной:
задана в параметрической форме, поэтому следует воспользоваться формулой для параметрической производной:
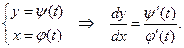
Получаем:
 ,
,
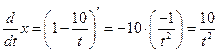 ,
,
откуда
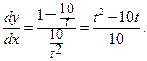
Задача 2.2.з 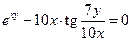 .
.
Решение. Функция 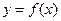 задана неявным уравнением. Чтобы найти производную
задана неявным уравнением. Чтобы найти производную 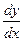 , продифференцируем тождество
, продифференцируем тождество 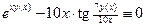 . Получаем:
. Получаем:
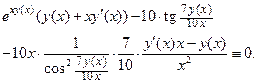
Перегруппируем слагаемые, выделяя члены, содержащие производную 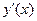 :
:
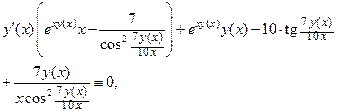
откуда следует, что
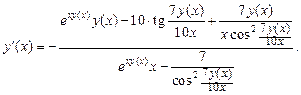
Линейная алгебра и аналитическая геометрия.
Дата: 2018-12-21, просмотров: 314.