1. Плоскошлифовальный станок
2. Заготовки типа пластина
3. Прибор для измерения волнистости обработанной поверхности
4. Персональный компьютер.
СОДЕРЖАНИЕ РАБОТЫ
1. По данным матрицы центрального композиционного ортогонального планирования второго порядка назначить режимы резания для обработки заготовки.
2. Выполнить обработку плоскостей деталей на уровнях, соответствующих звездным точкам и основному уровням факторов.
3. Измерить волнистость обработанных поверхностей.
4. Обработать результаты экспериментов.
5. Проверить значимость коэффициентов уравнения регрессии.
6. Проверить уравнение регрессии на адекватность.
7. Построить графики зависимостей волнистости обработанной поверхности от независимых факторов.
ОФОРМЛЕНИЕ ОТЧЕТА И СДАЧА ЗАЧЕТА
ПО ЛАБОРАТОРНОЙ РАБОТЕ
После выполнения всех пунктов раздела 6 студент оформляет отчет по лабораторной работе, в котором приводятся кратко теоретические положения, матрица центрального композиционного планирования второго порядка, заполненная с учетом результатов проведенных экспериментов и результатов измерения волнистости шлифованных поверхностей. В отчете приводятся расчеты, на основании которых получена многофакторная модель второго порядка.
Приводится проверка значимости коэффициентов уравнения регрессии и адекватности модели второго порядка, а также графики зависимостей, связывающих параметр оптимизации с независимыми факторами.
Отчет студента по лабораторной работе состоит в правильных ответах студента на вопросы преподавателя, касающихся как методики планирования, постановки и проведения экспериментов, их статистической обработки, так и объяснения физической сущности влияния того или иного фактора на параметр оптимизации.
Лабораторная работа № 4
«Оптимизация параметров методом крутого восхождения по поверхности отклика»
Цель работы: изучение и освоение методики отыскания оптимума функции, полученной в результате практической реализации плана первого или второго порядка и адекватно описывающей изучаемый процесс.
Задание
1. Для полученного в результате выполнения лабораторных работ №№1-3 уравнения регрессии, связывающего исследуемый параметр с независимыми факторами, найти оптимальное значения функции отклика.
2. Изучить методику расчета шага каждого фактора при крутом восхождении по поверхности отклика,
3. Выполнить крутое восхождение по поверхности отклика и добиться оптимального значения исследуемого параметра.
4. Построить графики зависимостей оптимального параметра обработанной поверхности от независимых факторов для адекватной линейной модели или модели второго порядка.
ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Под математической моделью понимают вид функции отклика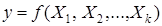 
. Выбор модели зависит от задачи исследования и от предъявляемых требований к модели.
Экстремальные задачи часто решают, используя шаговый метод. В этом случае модель должна удовлетворять требованиям этого метода.
В основе шагового метода лежит предположение, что совокупность значений параметра оптимизации у, полученная при различных сочетаниях значений факторов Xi, образует поверхность отклика.
Для наглядности представления о поверхности отклика при наличии Ymax рассмотрим простейший случай, при котором число факторов равно двум (X 1 и Х2).
Для каждого фактора установлены два значения: максимальное и минимальное. Между этими значениями каждый фактор может изменяться непрерывно или дискретно.
Границы значений факторов образуют на плоскости Х 1 0Х 2 (рис. 1), прямоугольник ABCD , внутри которого лежат точки возможных значений X 1 и Х2.
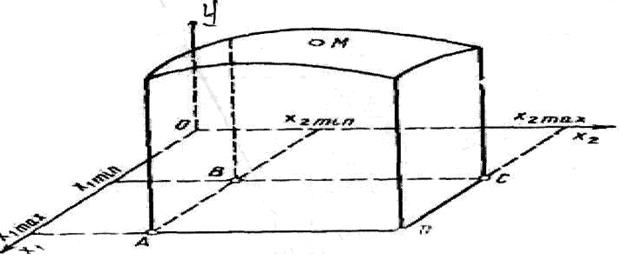Рис. 1. Поверхность отклика
Если по оси у откладывать значения Yi полученные при различных сочетаниях значений факторов, то точки Yi будут лежать .на поверхности отклика.
На этой поверхности будет находиться точка М, соответствующая оптимальному значению у. Для нахождения этой точки необходимо шаг за шагом двигаться по поверхности отклика.
Шаговый метод исходит из предположения, что поверхность отклика является гладкой и имеет единственный оптимум. Поверхность отклика расположена в k +1–мерном пространстве, которое называют факторным.
Факторное пространство зависит от числа k факторов. При большом числе факторов это пространство является многомерным, и геометрическая интерпретация функции отклика становится невозможной.
Для описания в многомерном пространстве поверхности отклика пользуются языком алгебры. Гладкость поверхности отклика и наличие на ней одной точки оптимума позволяют двигаться к последней в любом направлении, независимо от исходной точки.
При шаговом методе каждому фактору придают два значения: максимальное и минимальное. Эти значения составляют только часть возможных значений факторов.
На первом этапе реализации шагового метода выбирается лишь какая-то подобласть из области возможных значений факторов, и в этой подобласти ставится эксперимент.
На основании результатов этого эксперимента строится первая модель, по которой предсказываются отклики для значений факторов, выходящих за пределы выбранной подобласти.
Чем дальше от этой подобласти лежит точка, определяющая значения факторов, тем с меньшей точностью путем экстраполяции можно предсказать значение отклика для этой точки. Поэтому экстраполяцию производят вблизи подобласти эксперимента и используют ее для выбора условий проведения следующего эксперимента, т. е. устанавливают новые интервалы значений факторов или выбирают новую подобласть факторного пространства.
Поставив новый эксперимент, строят вторую модель и на основании ее делают следующий шаг в направлении к оптимуму. В этом и заключается сущность шагового метода.
Исходя из сущности этого метода к модели предъявляется главное требование, заключающееся в способности модели «предсказывать» направление дальнейших опытов с требуемой точностью. Это означает, что предсказанные по модели значения отклика должны отличаться от фактических не более, чем на некоторую наперед заданную величину.
Модель, удовлетворяющую этому требованию, называют адекватной. Если имеется несколько удовлетворяющих
указанному требованию моделей, то из них выбирается наиболее простая. Наиболее простой моделью является полином. Полином линеен относительно неизвестных коэффициентов, что упрощает обработку наблюдений.
Полином может быть первой, второй и более высокой степени, коэффициенты полинома вычисляют по результатам опытов. Чем больше число коэффициентов в полиноме, тем большее количество опытов необходимо поставить для их определения. Число коэффициентов зависит от степени полинома: чем выше степень, тем больше число коэффициентов. На первом этапе планирования – определении направления движения к оптимуму и крутого восхождения по поверхности отклика – наиболее целесообразно неизвестную функцию отклика аппроксимировать полиномом первой степени. Аппроксимация – это замена одной функции другой функцией, в каком-то смысле эквивалентной первой.
Полином первой степени имеет минимальное число коэффициентов при данном числе факторов и содержит необходимую информацию о направлении градиента, под которым понимают направление наискорейшего улучшения параметра оптимизации.
После достижения путем постепенного перемещения по поверхности отклика подобласти, в которой лежит точка оптимума, иногда для более полного описания подобласти переходят от полинома первой степени к полиному второй степени.
Движение по градиенту обеспечивает наиболее короткий путь к оптимуму, так как направление градиента – это направление самого крутого склона, ведущего от данной точки к вершине. Если изменять факторы пропорционально их коэффициентам с учетом знака, то движение к оптимуму будет осуществляться по самому крутому пути.
Этот процесс движения к области оптимума называют крутым восхождением. Технику расчета крутого восхождения рассмотрим на примере задачи с одним фактором X 1 (рис.2). Предположим, что кривая 1 представляет собой неизвестную функцию отклика. В результате реализации плана эксперимента с центром в точке О получено уравнение регрессии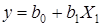 
адекватно описывающее функцию отклика в области значений фактора X 1 от –1 до +1.
Значение коэффициента регрессии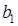 
равно тангенсу угла между линией регрессии и осью данного фактора. Если шаг движения по оси x 1 принять равным 
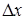, то, умножив его на 
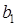, получим координаты ( 
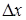и 
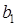
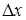) точки А, лежащей на градиенте.
После второго шага расстояние по оси x 1 будет равно 2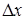 
. Умножив 2 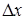на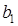 
, найдем координаты 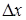2 ; и 2 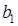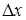точки В, лежащей на градиенте, и т. д. Затем проводят опыты с условиями, отвечающими точкам на градиенте. По результатам этих опытов определяют область оптимума.
В практических задачах для сокращения объема эксперимента проводят не все, а только часть опытов, предусмотренных крутым восхождением. Условия опытов выбирают так, чтобы область оптимума можно было заключить в «вилку». После этого опыты проводят в точках интервала, образованного точками «вилки», до нахождения наилучшего результата.
 |
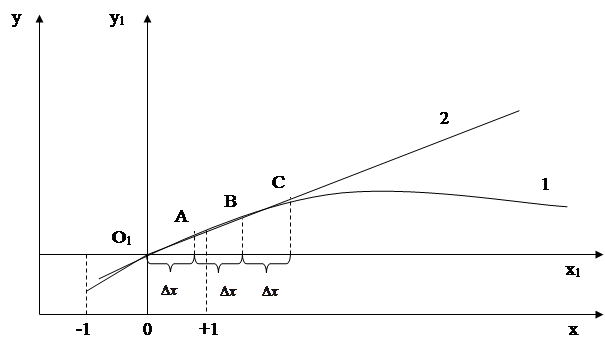Рис.2 Схема к расчету координат точек в направлении градиента: 1-график функции отклика; прямая направления градиента.
В случае k факторов расчет крутого восхождения по оси каждого фактора производят аналогичным образом, так как коэффициенты bi определяются независимо друг от друга.
При этом движение по осям осуществляют одновременно.
Шаг движения по градиенту выбирают таким, чтобы его минимальная величина была больше ошибки, с которой фиксируют фактор. Максимальную величину шага ограничивает область определения фактора.
Необходимо учитывать, что при движении к оптимуму малый шаг потребу значительного числа опытов, а большой шаг может привести к проскоку области оптимума.
Шаг движения выбирают для одного фактора, а для остальных его рассчитывают по выражению
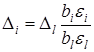
где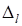 
– выбранный шаг движения для фактора l; 
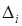– шаг движения дл: i-го фактора; 
, 
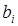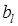– коэффициенты регрессии i-го и l-го факторов; 
, 
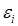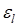– интервалы варьирования i-го и l-го факторов.
Движение по градиенту должно начинаться от нулевой точки основного уровня каждого фактора, так как коэффициенты регрессии вычислены дл. функции отклика, разложенной в ряд Тейлора в окрестности нулевой точки.
Если коэффициенты регрессии значительно отличаются друг от друга, то рекомендуют изменить интервалы варьирования факторов и провести новую серию опытов, ибо при различии коэффициентов на порядок и боле! многофакторный эксперимент при крутом восхождении может превратиться однофакторный.
Рассчитав шаг движения для каждого фактора, находят условия: «мысленных» опытов. «Мысленными» называют опыты, условия, проведения которых на стадии крутого восхождения установлены с учетом шаг; движения для каждого фактора.
С целью проверки результатов крутого восхождения часть мысленных опытов реализуется.
Если при движении к оптимуму возникает ситуация, препятствующая изменению каких-либо факторов, то эти факторы можно фиксировать на оптимальных уровнях, продолжая движение по стальным факторам.
Крутое восхождение прекращается, если найдены условия оптимизации или если ограничения на факторы делают дальнейшее движение по градиент неразумным.
Рассмотренный метод крутого восхождения в область оптимума носит название метода Бокса – Уилсона.
2.СОДЕРЖАНИЕ РАБОТЫ
1. По полученной ранее адекватной модели найти экстремальное значение параметра оптимизации.
2. Выбрать фактор, наиболее существенно влияющий на параметр оптимизации, и назначить шаг, с которым он будет изменяться фактор при крутом восхождении по поверхности отклика.
3. Рассчитать шаг движения по градиенту для остальных факторов.
4. Рассчитать факторы для мысленных и реализованных опытов при крутом восхождении в область оптимума.
Для выполнения пунктов 3 и 4 удобно пользоваться примером – таблицей.
Таблица
Расчет крутого восхождения
| Наименование | X1 | Х2 | X3 | y |
| Основной уровень | 0,40 | 840 | 60 | – |
Коэффициент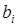 
| 20 | 11,9 | –5.1 | – |
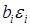
| 0,15 | 100 | 60 | – |
Интервал варьирования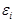 
| 3 | 1190 | –306 | – |
| Шаг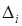
| 0,0252 | 10 | –2,57 | – |
| Округленный шаг | 0,03 | 10 | –3 | – |
| Мысленный опыт | 0,43 | 850 | 57 | – |
| То же | 0,46 | 860 | 54 | – |
| Реализованный опыт | 0,49 | 870 | 51 | 108 |
| Мысленный опыт | 0,52 | 880 | 48 | – |
| То же | 0,55 | 890 | 45 | – |
| Реализованный опыт | 0,58 | 900 | 42 | 196 |
| Реализованный опыт | 0,61 | 910 | 39 | 366 |
| Реализованный опыт | 0,64 | 920 | 36 | 313 |
Как следует из таблицы лучший результат (оптимальное значение параметра у) получен в предпоследнем опыте. Величина параметра оптимизации достигла своего максимального значения у =366, на этом работа была закончена, так как цель многофакторного эксперимента достигнута.
ОФОРМЛЕНИЕ ОТЧЕТА И СДАЧА ЗАЧЕТА
ПО ЛАБОРАТОРНОЙ РАБОТЕ
После выполнения всех пунктов раздела 4 студент оформляет отчет по лабораторной работе, в котором приводятся кратко теоретические положения, расчеты шагов факторов при кругом восхождении по поверхности отклика. Рассчитываются значения факторов, как в мысленных, так и реализуемых опытах.
Отчет студента по лабораторной работе состоит в правильных ответах студента на вопросы преподавателя, касающихся как методики крутого восхождения по поверхности отклика, так и проведения экспериментов, их статистической обработки, а также объяснения физической сущности влияния того или иного фактора на значение параметра оптимизации.
Оглавление
1 .Предисловие...................................................................................... ...…3
2.Лабораторная работа №1. Планирование и реализация линейных полнофакторных экспериментов................................................................. …...4
3.Лабораторная работа №2. Планирование и реализация линейных дробных факторных экспериментов......................................................................... ……19
4.Лабораторная работа №3. Планирование и реализация центрального композиционного рототабельного многофакторного эксперимента второго порядка..................................................................................................................... …...26
5.Лабораторная работа №4. Оптимизация параметров методом крутого восхождения по поверхности отклика…………………………………………….32
Дата: 2018-12-21, просмотров: 245.
