План типа 23-1 может быть представлен двумя полурепликами (табл. 3), которые задаются одним из следующих генерирующих соотношений:
 (1)
(1)
Генерирующие соотношения умножим на новую независимую переменную х3:
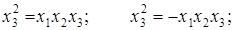 (2)
(2)
Таблица 3
Две полуреплики 23-1
| Номер опыта | X3= X1 X2 | Номер опыта | X3= –X1 X2 | ||||
| X1 | X2 | Х3 | X1 | X2 | Х3 | ||
| 1 | – | + | – | 1 | – | + | + |
| 2 | + | + | + | 2 | + | + | – |
| 3 | – | – | + | 3 | – | – | – |
| 4 | + | – | – | 4 | + | – | + |
Поскольку всегда 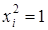 , то получим следующие выражения:
, то получим следующие выражения:
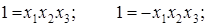 (3)
(3)
В результате умножения генерирующего соотношения на новую переменную получают так называемый определяющий контраст. Для указанных выше полуреплик определяющими контрастами будут выражения (3). Зная определяющий контраст, можно найти соотношения, задающие совместные оценки. Для этого необходимо помножить независимые переменные х1, х2 и х3 на определяющий контраст. Умножая определяющие контрасты (3) на х1; получим соотношения

Умножая определяющие контрасты на х2 и х3, получаем следующие соотношения


Это означает, что коэффициенты регрессии будут оценками
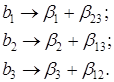
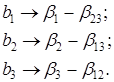
Определяющим контрастом полуреплики является соотношение
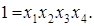
Совместные оценки будут определяться следующим образом: 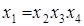
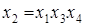
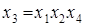
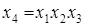
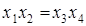
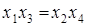
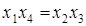
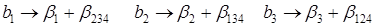
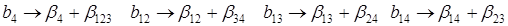
Таблица 4
Полуреплика 24-1 с определяющим контрастом 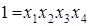
| Номер опыта | X0 | X1 | Х2 | Х3 | X4 | Y |
| 1 | + | – | – | + | + | Y1 |
| 2 | + | + | – | + | – | Y2 |
| 3 | + | – | + | + | – | Y3 |
| 4 | + | + | + | + | + | Y4 |
| 5 | + | – | – | – | - | Y5 |
| 6 | + | + | – | – | + | Y6 |
| 7 | + | – | + | – | + | Y7 |
| 8 | + | + | + | – | - | Y8 |
Таблица 5
Полуреплика 24-1 с определяющим контрастом 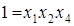
| Номер опыта | X0 | X1 | Х2 | Х3 | X4 | Y |
| 1 | + | – | – | + | + | Y1 |
| 2 | + | + | – | + | – | Y2 |
| 3 | + | – | + | + | – | Y3 |
| 4 | + | + | + | + | + | Y4 |
| 5 | + | – | – | – | + | Y5 |
| 6 | + | + | – | – | – | Y6 |
| 7 | + | – | + | – | – | Y7 |
| 8 | + | + | + | – | + | Y8 |
Полуреплика 24-1 может быть также задана генерирующим соотношением X4= X1 Х2. Матрица планирования этой полуреплики представлена в табл. 5.
Определяющим контрастом полуреплики является соотношение
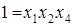
Совместные оценки в этом случае будут следующие:
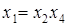
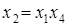
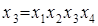
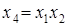
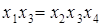
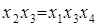
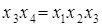
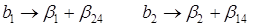
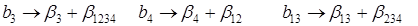
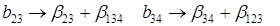
В практических задачах тройные и более высокого порядка взаимодействия значительно чаще, чем двойные, бывают равны нулю, и ими обычно можно пренебречь .
Полуреплика 24-1, заданная генерирующим соотношением 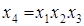 , позволяет получить раздельные оценки четырех линейных эффектов и три совместные оценки парных взаимодействий. В этом случае раздельными оценками будут
, позволяет получить раздельные оценки четырех линейных эффектов и три совместные оценки парных взаимодействий. В этом случае раздельными оценками будут 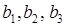 и
и 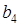 так как тройными взаимодействиями, вследствие их незначимости, можно пренебречь. В полуреплике, заданной генерирующим соотношением
так как тройными взаимодействиями, вследствие их незначимости, можно пренебречь. В полуреплике, заданной генерирующим соотношением 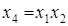 , три линейных эффекта, а именно
, три линейных эффекта, а именно 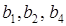 – оказались смешанными с парными взаимодействиями.
– оказались смешанными с парными взаимодействиями.
Разрешающая способность полуреплики, заданной генерирующим соотношением 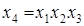 получилась значительно выше, чем у полуреплики, заданной генерирующим соотношением
получилась значительно выше, чем у полуреплики, заданной генерирующим соотношением 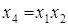 . Следовательно, разрешающая способность полуреплики зависит от генерирующего соотношения, которым она задана.
. Следовательно, разрешающая способность полуреплики зависит от генерирующего соотношения, которым она задана.
Таким образом, получили весьма сложную систему смешивания. Все линейные эффекты оказались смешанными с несколькими парными взаимодействиями, поэтому разрешающая способность дробной реплики очень низкая. Пользоваться такой репликой можно лишь в том случае, если все парные взаимодействия близки к нулю.
Выбор дробной реплики зависит от конкретной задачи. Для получения линейной модели рекомендуют выбирать дробные реплики с возможно большей разрешающей способностью, т. е. реплики, у которых линейные эффекты смешаны с эффектами взаимодействия, близкими к нулю. При выборе дробной реплики важно учитывать насыщенность плана, т. е. соотношение между числом опытов и числом коэффициентов, определяемых по результатам этих опытов.
Дробная реплика, полученная заменой всех эффектов взаимодействия новыми факторами, называется насыщенной. Применение насыщенных планов требует минимального числа опытов.
Число опытов в матрице насыщенной дробной реплики равно числу коэффициентов линейной модели. Дробные реплики широко применяют при получении линейных моделей. Эффективность применения дробных реплик зависит от удачного выбора системы смешивания линейных эффектов с эффектами взаимодействия.
При построении дробных реплик используют следующее правило: новый фактор, введенный в планирование, нужно поместить в столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь.
Дата: 2018-12-21, просмотров: 356.