Цель работы: изучение и освоение методики составления и практической реализации плана первого порядка дробного факторного эксперимента.
Задание
1. Для условий плоского шлифования детали на плоскошлифовальном станке определить факторы, влияющие на волнистость обработанной поверхности;
2. Определить основной, нижний и верхний уровни факторов, а также интервал варьирования;
3. Закодировать факторы и составить план дробного факторного эксперимента и матрицу планирования;
4. Реализовать матрицу планирования, предварительно рандомизировав проведение экспериментов во времени;
5. Рассчитать коэффициенты регрессии и проверить их значимость;
6. Проверить гипотезу адекватности найденной линейной модели, связывающей волнистость обработанной поверхности с независимыми факторами.
7. Построить графики зависимостей волнистости обработанной поверхности от независимых факторов.
ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
При большом числе факторов (к>3) проведение полного факторного эксперимента связано с большим числом опытов, значительно превосходящим число коэффициентов линейной модели. Если при получении модели можно ограничиться линейным приближением, т. е. получить адекватную модель в виде полинома 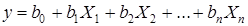 , то число опытов можно резко сократить в результате применения дробного факторного эксперимента.
, то число опытов можно резко сократить в результате применения дробного факторного эксперимента.
Таблица 1
Матрица планирования
| Номер опыта | X0 | X1 | Х2 | Х3(X1 Х2) | Y |
| 1 | + | + | + | + | Y1 |
| 2 | + | – | + | – | Y2 |
| 3 | + | + | – | – | Y3 |
| 4 | + | – | – | + | Y4 |
Так, например, в полном факторном эксперименте типа 22 при линейном приближении коэффициент регрессии b 12 можно принять равным нулю, а столбец X1 Х2 матрицы (табл. 1) использовать для третьего фактора Х3.
В этом случае линейная модель будет выражаться уравнением 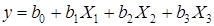 . Для определения коэффициентов этого уравнения достаточно провести четыре опыта вместо восьми в полном факторном эксперименте типа 23.
. Для определения коэффициентов этого уравнения достаточно провести четыре опыта вместо восьми в полном факторном эксперименте типа 23.
План эксперимента, предусматривающий реализацию половины опытов полного факторного эксперимента, называют полурепликой. При увеличении числа факторов (к>3) возможно применение реплик большей дробности.
Дробной репликой называют план эксперимента, являющийся частью плана полного факторного эксперимента. Дробные реплики обозначают выражением 2 k -р , где р – число линейных эффектов, приравненных к эффектам взаимодействия. При р = 1 получают полуреплику; при р = 2 получают 1/4-реплику; при р = 3 получают 1/8-реплику и т. д. по степеням двойки.
Так, например, если в полном факторном эксперименте 23 (табл. 2) один из эффектов взаимодействия (Х1Х2, Х1ХЗ, Х2ХЗ, Х1Х2ХЗ) заменим четвертым фактором Х4 то получим полуреплику 24-1 от полно факторного эксперимента 24. Если два эффекта взаимодействия заменить факторами Х4 и Х5, то получим 1/4 – реплику 25-2 от полного факторного эксперимента 25. Можно получить 1/8 – реплику от полного факторного эксперимента, заменив три эффекта взаимодействия факторами Х4, Х5 и Х6.
Таблица 2
Матрица полного факторного эксперимента типа 23
| Номер опыта | X0 | X1 | Х2 | Х3 | X1 Х2 | X1 Х3 | X2 Х3 | X1 Х2 Х3 | Yi |
| 1 | + | – | – | + | + | – | – | + | Y1 |
| 2 | + | + | – | + | – | + | – | – | Y2 |
| 3 | + | – | + | + | – | – | + | – | Y3 |
| 4 | + | + | + | + | + | + | + | + | Y4 |
| 5 | + | – | – | – | + | + | + | – | Y5 |
| 6 | + | + | – | – | – | – | + | + | Y6 |
| 7 | + | – | + | – | – | + | – | + | Y7 |
| 8 | + | + | + | – | + | – | – | – | Y8 |
Если заменить четыре эффекта взаимодействия факторами Х4, Х5 и Х6 и Х7, то получим 1/16 – реплику 27-4 от полного факторного эксперимента 27. Реплики, которые используют для сокращения числа опытов в 2m раз, где т = 1, 2, 3, ..., называют регулярными.
В связи с тем, что в дробных репликах часть взаимодействий заменена новыми факторами, то найденные коэффициенты уравнения регрессии будут являться совместными оценками линейных эффектов и эффектов взаимодействия.
Коэффициенты 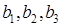 будут оценками совмещенных эффектов, а именно
будут оценками совмещенных эффектов, а именно
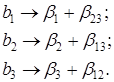
Коэффициент b 1 является оценкой влияния фактора X1 и парного взаимодействия X2X3 на функцию отклика. Влияние фактора X1 в этом случае характеризуется величиной 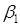 , а влияние взаимодействия – величиной
, а влияние взаимодействия – величиной 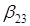 . Оценки, в которых невозможно разделить линейный эффект и эффект взаимодействия, называют смешанными. Линейные эффекты рекомендуется смешивать, прежде всего, с их взаимодействиями, которые согласно априорной информации незначимы.
. Оценки, в которых невозможно разделить линейный эффект и эффект взаимодействия, называют смешанными. Линейные эффекты рекомендуется смешивать, прежде всего, с их взаимодействиями, которые согласно априорной информации незначимы.
Дата: 2018-12-21, просмотров: 338.