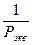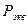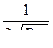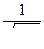Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

При проектировании высотных одиночных ходов между исходными пунктами опорной высотной сети, если геометрические параметры ходов (периметры) не укладываются в установленные допуски, следует делать расчет необходимой точности измерения превышений на километр хода ( 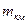) или на станции ( ), исходя из требуемой точности определения высот точек ( 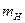) проектируемого хода.

Расчет необходимой точности измерений превышения можно произвести в следующем порядке.

Согласно (4.1):

                                            ,

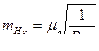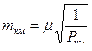                                            ,      (4.21)

                                       ,

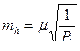где 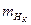- ожидаемая средняя квадратическая ошибка высоты точки К, расположенной в слабом месте хода,

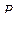– вес точки К, расположенной в наиболее слабом месте хода (наиболее удаленной от исходных пунктов).

Согласно (4.21) можно выразить значения :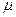

                                            ,

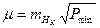                                            ,                (4.22)

                                            ,

 

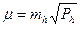и, соответственно, с учетом (1.2.22) составить уравнения:

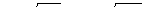                                            ,            (4.23)

                                            .             (4.24)

Задаваясь допустимым значением для 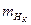( 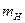), согласно уравнениям (4.23), (4.24) можно установить необходимую точность измерения превышений:

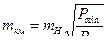                                       ,                    (4.25)

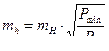                                            .                   (4.26)

Формулы (4.25), (4.26) достаточно строги, так как веса измеренных и уравненных превышений отличаются мало, вследствие того, что в высотном ходе имеется только одно избыточное измерение превышения.

Для упрощения проектирования высотных ходов в отдельных случаях, не предусмотренных нормативными допусками, следует устанавливать геометрические параметры ходов, в первую очередь допустимую длину высотных ходов или допустимое количество станций в ходе, которые можно рассчитать в следующем порядке.

Ожидаемая средняя квадратическая ошибка (невязка) одиночного хода вычисляется по формулам:

 

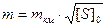                                            ,                    (4.27)

                                            ,                         (4.28)

где 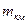 - ошибка измерения превышений на километр хода,

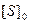- периметр хода в километрах,

 - ошибка измерения превышения на станции,

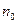 - число станций в ходе.

Принимая ошибку уравненной высоты точки К в наиболее слабом месте хода аналогично (4.4) и, задаваясь допустимым значением ошибки определения высот точек хода ( 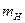), с учетом (4.4), (4.27), (4.28), получим искомые допуски для одиночного нивелирного хода:

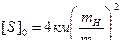                                            ,                 (4.29)

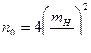                                            .                       (4.30)

Таким образом, необходимую точность измерения превышений в одиночном нивелирном ходе можно установить на основе формул (4.25), (4.26), допустимую длину такого хода по формуле (4.30).

 

4.2.3 Проектирование систем плановых и высотных ходов с узловыми точками

 

Узловые точки в различных системах ходов не являются пунктами опорной сети и определяются с определенными погрешностями. Следовательно, хода в таких системах должны иметь допустимую длину меньшую, чем для одиночного хода между пунктами опорной сети при одинаковой точности измерений в них. И, соответственно, при одинаковой длине должны иметь более высокую точность угловых и линейных измерений для обеспечения одинаковой точности определения координат или высот относительно опорной сети.

Для применения первого принципа (метода) проектирования нормативными документами для некоторых типовых систем устанавливаются допуски на их геометрические параметры, обычно, через коэффициент к допускам для одиночных ходов.

Допуски могут быть получены специальными расчетами, которые приводятся ниже.

В качестве примера, установим производственные допуски для применения первого метода проектирования некоторых распространенных систем ходов с узловыми точками (рис. 4.1а, 4.2а, 4.3а, 4.4а, 4.5а).

 

 

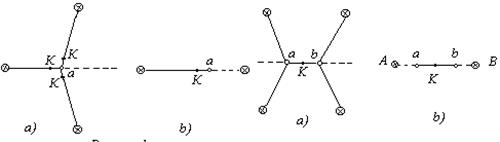
Рисунок 4.1- Система 1     Рисунок 4.2 – Система 2

 

Рисунок 4.3 – Система 3

 

 

 

 

                                                                             

Рисунок 4.4 –Система 4

 

 

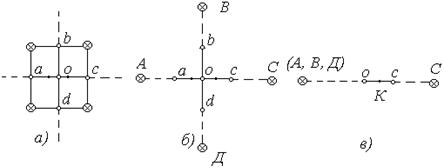
Рисунок 4.5 – Система 5

 

На рисунках 4.1-4.5 показаны этапы эквивалентных преобразований, сводящих системы к одиночным ходам, опирающимся на один или два твердых пункта.

Преобразования выполнены с таким расчетом, чтобы в процессе эквивалентных замен ход, включающий слабое место системы, или сама точка К с ожидаемой максимальной ошибкой, оставались реальными.

Подобное правило эквивалентных преобразований при проектировании рекомендуется в научно- технической литературе. Несоблюдение этого правила обязательно приводит к завышению ожидаемой точности проектируемой сети, т. е. может вызвать недоброкачественность результатов работ.

В результате эквивалентных преобразований систем ходов (рис. 4.1 – 4.5) установлены веса одиночных ходов, эквивалентных системам - Р_экв, веса узловых точек - Р_узл и местоположение точки К (слабого места систем) относительно узловых точек i (а, b , с, d ) через расстояние [S]_{i к} (табл.4.1).

В таблице 4.1 номера систем соответствуют количеству узловых точек в системе и номерам рисунков; через п обозначено число ходов одинаковой длины [S] и весом, равным единице, сходящихся от твердых пунктов в узловых точках а, b , с, d .

 

С учетом Р_экв и Р_узл (табл.4.1) основные показатели систем могут быть вычислены по формулам:

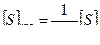,                              (4.31)

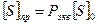,                               (4.32)

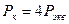,                                    (4.33)

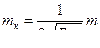,                              (4.34)

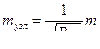,                              (4.35)

 

где [ S ]_экв —длина хода, эквивалентного системе;

 

[S]_пр — допустимая длина ходов системы между узловыми, а также между узловыми и твердыми пунктами;

 

[S]₀ — допустимая длина одиночного хода между твердыми пунктами;

m_узл—ошибка уравненного положения узловых точек;

 

[S] и m— длина и ошибка хода (в системах) с весом, равным единице.

 

Численные значения коэффициентов при [S], [S]₀ и m в формулах (4.31 – 4.35) приведены в таблице 4.1.

Таблица 4.1

Результаты эквивалентных преобразований систем ходов с узловыми точками

Система	Рэкв	Рузл	[S] i к
1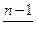
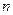
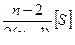
2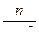
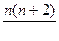
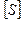
3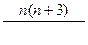
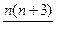
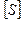
4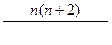
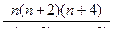
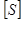
5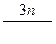

 

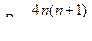
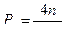
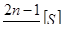
Данные таблицы 4.1 показывают, что увеличение числа п в большей степени влияет на повышение точности определения узловых точек и в меньшей - на точность определения точек, расположенных в слабых местах систем. Следовательно, для уменьшения значений т_к в первую очередь следует стремиться к уменьшению длины ходов [S], а затем к увеличению числа п.

Основным производственным допуском при проектировании систем является предельная длина ходов [S]_np. Для рассмотренных систем, согласно табл.4.1, она зависит от величины Р_экв и находится в пределах от 0,40 [S]₀ до 0,75 [S]₀, т. е. единого допуска устанавливать нельзя. В технической же литературе часто приводится только один допуск без указания вида систем, причем в разных источниках он колеблется от 0,5 [S]₀ до [S]₀.

 

Для установления местоположения слабого места системы ходов одинаковой длины [S] с одной узловой точкой рекомендована формула,

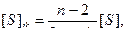                  (4.36)

где 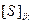- расстояние от узловой точки i до слабого места системы (точки k); n – число ходов от исходных пунктов, сходящихся в узловой точке.

Следует отметить, что многие программы уравнивания на ЭВМ плановых и высотных ходов предусматривают оценку точности положения только узловых точек, то есть не оценивают наиболее слабые места систем.

Для рассматриваемых в качестве примера, систем можно сделать следующие выводы:

- основные показатели систем и допуски, приведенные в таблицах 4.1 и 4.2, с учетом формул (4.31-4.35), могут быть использованы как при первом, так и втором методах проектирования;

- допустимая длина ходов в рассмотренных системах колеблется от 0,40 до 0,75 предельной длины одиночного хода между исходными пунктами, что в ряде случаев значительно расходится с инструктивными допусками и требует уточнения последних;

 

Таблица 4.2

Значения коэффициентов к вычислениям по формулам (4.31-4.35)

Значения	При	Для систем
		1	2	3	4	5
	1			2,50	2,33
	2		2,00	1,80	1,75	2,00
	3	1,50	1,67	1,56	1,53	1,78
	4	1,33	1,50	1,43	1,42	1,67
	1			0,40	0,43
	2		0,50	0,56	0,57	0,50
	3	0,67	0,60	0,65	0,65	0,56
	4	0,75	0,67	0,70	0,70	0,60
	1				0,79	0,76
	2		0,71	0,57	0,66	0,71
	3	0,61	0,64	0,62	0,62	0,67
	4	0,58	0,61	0,60	0,60	0,64
	1			0,71	0,68	--
	2		0,61	0,55	0,54	0,61 (0,61)*
	3	0,58	0,52	0,47	0,47	0,58 (0,52)*
	4	0,50	0,46	0,42	0,42	0,56 (0,46)*

 

- для уменьшения ошибки определения точки, расположенной в слабом месте системы, в первую очередь следует стремиться к уменьшению длины ходов, а затем к увеличению числа ходов, сходящихся в узловых точках;

- эквивалентные преобразования при проектировании следует производить с таким расчетом, чтобы точка в слабом месте системы или ход, включающий ее, оставались реальными.

При втором принципе (методе) проектирования установление необходимой точности измерений в системе ходов с узловыми точками можно производить как и для одиночных ходов по формулам (4.9, 4.16, 4.17, 4.25, 4.26), если привести систему ходов путем эквивалентных преобразований к одиночному ходу, включающему наиболее слабое место системы, вычислив значение .

В случае, если слабое место системы найти затруднительно, то следует отыскать вариант наиболее длинного эквивалентного хода с установлением для него .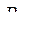

 При расчетах по формулам (4.16), (4.17) следует учесть выражения:

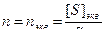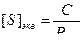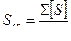      ;   ;     .      (4.37)

Для нахождения веса точки в наиболее слабом месте системы ходов ( 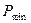), если веса при проектировании не вычисляются строгим методом, например, с получением обратной матрицы весов на ЭВМ, можно для простых систем применить, кроме способа эквивалентной замены, известные методы полигонов или узлов, разработанные профессором В.В. Поповым для уравнивания систем ходов.

Так, например, обратный вес уравненного планового или высотного положения любой точки F в системе ходов, вес которых отражает формула (4.7), можно вычислить по рабочей формуле:

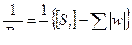                         ,                                 (4.38)

 где 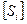-длина ходовой линии от исходного пункта до оцениваемой точки К,  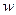   - поправка на звенья ходовой линии, полученная при разбрасывании свободных членов переходных уравнений по методу полигонов проф. В.В. Попова; при этом, свободные члены переходных уравнений для полигонов приравниваются к периметру участка ходовой линии, соприкасающегося с полигонами, со знаками противоположными по обе стороны ходовой линии.

 

5. ГЕОДЕЗИЧЕСКИЕ РАЗБИВОЧНЫЕ РАБОТЫ

 

5.1Способы построения на местности планового проектного положения точек

На практике применяется несколько способов построения на местности планового положения точек: способ прямоугольных координат, способ полярных координат, способ линейной засечки, способ прямой угловой засечки, способ пересечения створов и другие. Выбор того или иного способа зависит от вида геодезической основы на строительной площадке, характера возводимого сооружения, особенностей местности и ряда других причин.

Реализация выбранного способа разбивки заключается в последовательном выполнении отдельных элементов разбивочных работ, прежде всего, в построении на местности заданных углов и расстояний. Для контроля выносимой на местность точки ее положение определяют каким-либо другим способом или тем же способом, но от других опорных пунктов.

Полевые разбивочные и контрольные работы выполняются на основе разбивочных чертежей, которые составляются по результатам специальных расчетов, где в качестве исходных данных берут координаты опорных и проектных точек.

 

Построение проектного угла

Перенесение горизонтального угла на местность может быть выполнено теодолитом двумя способами: с точностью, равной точности теодолита и с точностью превышающей точность теодолита. Сводится к построению на местности стороны и угла 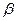 от исходной стороны.

 

 

Рис. 1.5.3 - Схемы построения проектного угла двумя способами

 

Используя первый способ проектный угол β откладывают (дважды) от исходного направления АВ (Рис. а) теодолитом при двух положениях круга и отмечают на местности точки С₁ и С₂. Из-за влияния ошибок вынесенные точки не совпадают. На местности закрепляют вычисленное расстояние С=(С₁+С₂)/2. Полученный таким образом угол АВС = β будет отличаться от проектного его значения не более чем на величину точности теодолита.

При построении проектного угла вторым способом, теодолитом при одном положении круга откладывают на местности значение угла и закрепляют полученное направление точкой С_о. Далее, несколькими полными приемами, измеряют угол ВАС_о и получают его значение β_изм. с повышенной точностью (рис. В). Зная величину проектного угла β_пр., находят разность

                             ∆β= β_пр- β_изм.

 

Измерив расстояние АС_о =d, вычисляют линейное смещение р

                                      .

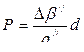Величину р откладывают от перпендикуляра к линии АС_о и закрепляют точку С. Полученный таким образом угол ВАС для контроля измеряют тем же числом приемов, что и угол ВАС_о.

Построение на местности проектного расстояния. Перенесение проектного расстояния заключается в отложении на местности проектной линии от исходной точки в заданном направлении. С этой целью на местности следует отложить расстояние D, горизонтальное проложение d которого равно проектному. В проектное расстояние вводятся поправки за наклон местности (∆ν), температуру (∆t), компарирование (∆к), за переход от плоскости проекции Гаусса- Крюгера к земной поверхности (∆г) и имеет следующий вид:

S =S_пр +∆ν +∆t +∆к +∆г.

Поправка за наклон линии всегда вводится со знаком (+). Если на плане по горизонталям или на местности нивелированием определено превышение, то поправка за наклон определяется по формуле ∆ν = .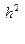

Поправка температуру: ∆t = α D₀(t-t₀), где α - коэффициент линейного расширения материала мерного прибора (для стали α = 0,000012); t,t₀ – соответственно температура мерного прибора при измерениях и при компарировании.

Поправка за компарирование ∆к = 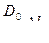, где l –длина мерного прибора, ∆l_{k –} поправка за компарирование на длину мерного прибора.

Следует помнить, что при откладывании проектной линии на местности все поправки имеют знаки, обратные знакам поправок при измерениях.

Для разбивки линий с точностью 1:2000-1:3000 применяют стальные мерные ленты или рулетки, 1:3000-1:10000- шкловые ленты и рулетки,1:10000-1:50000 – инварные ленты или светодальномеры.