При решении задач линейного программирования можно выделить пять следующих этапов:
1) постановка задачи, заключается в словесной формулировке задачи с
указанием цели и критерия оптимальности;
2) математическая формулировка задачи, которая заключается в
формализации постановки задачи, то есть, выражении её математическими символами в виде математической модели. Математическая модель включает функцию цели, систему
ограничений, представленные неравенствами и уравнениями;
3) сбор необходимых количественных данных и составление исходной
матрицы;
4) решение системы уравнений и неравенств, входящих в
математическую модель с учетом функции цели;
5) анализ и корректировка решения.
На четвертом этапе решение системы уравнений и неравенств может быть выполнено следующими способами:
-графическим;
-распределительным;
- симплексным и их модификациями.
Графический способ применяется для решения систем с двумя неизвестными, с тремя решение возможно, но затруднительно.
Распределительный способ в основном применяется для решения задач, имеющих транспортную модель. Такая модель имеет три особенности:
-все ограничения представлены в виде равенств;
- все коэффициенты при неизвестных равны 1;
- каждое неизвестное входит в два ограничения.
Распределительным способом решается до 40% задач математического программирования.
Симплексный способ является наиболее универсальным, используемым для решения любых задач.
2.6.3 Пример применения математического программирования для проектирования преобразования рельефа при вертикальной планировке улицы
На генеральном плане поселения исходная поверхность задана высотами земли 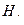 , требуется составить проект вертикальной планировки (преобразования рельефа) улицы с соблюдением следующих условий:
, требуется составить проект вертикальной планировки (преобразования рельефа) улицы с соблюдением следующих условий:
1) продольные уклоны отдельных участков улицы должны быть в пределах от 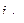 до
до 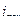 ;
;
2) поперечные уклоны двускатной улицы должны быть в пределах
пределах от 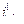 до
до 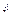 ;
;
3) разность уклонов на смежных участках не должна быть больше величины 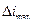 ;
;
4) проектная отметка в начале улиц должна быть равна отметке исходной поверхности, а проектная отметка в конце улицы не менее отметки исходной поверхности;
5) Объем выемки должен быть равен объему подсыпки.
Цель: требуется определить проектные отметки 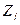 , удовлетворяющие всем указанным условиям и обращающие в min суммарный объем земляных работ.
, удовлетворяющие всем указанным условиям и обращающие в min суммарный объем земляных работ.

Рисунок 2.1. Фрагмент топографической поверхности улицы, описанный высотами пяти поперечников.
На рис.1 
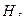 -отметки земли, характеризующие топографическую поверхность; l´ - расстояния между точками на поперечнике; l – расстояния между поперечниками.
-отметки земли, характеризующие топографическую поверхность; l´ - расстояния между точками на поперечнике; l – расстояния между поперечниками.
Формализуем условия , предъявленные к проекту. По продольным уклонам можно записать 12 неравенств вида 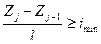 и 12 неравенств вида
и 12 неравенств вида 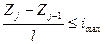 , при
, при 
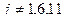 , всего 24 условия.
, всего 24 условия.
По поперечным уклонам запишем пять условий вида 

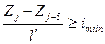 , пять условий вида
, пять условий вида 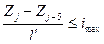 , пять условий вида
, пять условий вида 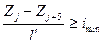 , пять
, пять 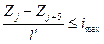 , при
, при 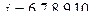 , всего 20 условий.
, всего 20 условий.
Третье условие можно записать в следующем виде 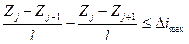 , при
, при 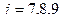 , таких условий возникает три.
, таких условий возникает три.
Четвертое условие запишем в виде уравнения и неравенства
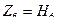 ;
;
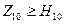 .
.
Условие равенства объемов земляных работ выражается формулой
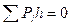 , где
, где 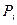 - вес рабочей отметки, равный площади выемки или подсыпки, а
- вес рабочей отметки, равный площади выемки или подсыпки, а 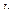 - рабочая отметка. Выразив рабочие отметки через принятые нами обозначения отметок топографической поверхности и проектных отметок получим уравнение для равенства объемов земляных работ
- рабочая отметка. Выразив рабочие отметки через принятые нами обозначения отметок топографической поверхности и проектных отметок получим уравнение для равенства объемов земляных работ 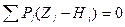 .
.
Цель решаемой задачи представим выражением 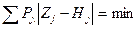 .
.
Полученная математическая модель содержит 48 неравенств и два равенства, то есть 50 уравнений и неравенств. Модель стандартной формы, для решения такой системы её нужно представить в канонической форме. Для этого в дополнение к 15 неизвестным вводится в каждое неравенство дополнительное (балансовое) неотрицательное неизвестное. Для неравенств типа 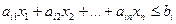 дополнительное неизвестное прибавляется
дополнительное неизвестное прибавляется 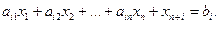
Для неравенств типа 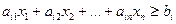 дополнительное неизвестное вычитается
дополнительное неизвестное вычитается 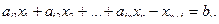
В результате таких действий получим 50 уравнений с 63 неизвестными (15+48), которые можно решить симплексным методом.
В результате получим проектные отметки всех точек модели, оптимально удовлетворяющие всем поставленным условиям и функции цели.
2.7 Характеристики планово-картографического материала, используемого для проектирования
Инженерно-геодезическое проектирование выполняется на топографической основе. В качестве основы выступают крупномасштабные топографические планы, реже карты (только на стадии предварительных изысканий- технико-экономического обоснования проекта).
При использовании графического и графоаналитического способов проектирования горизонтальной и вертикальной планировки, а так же при подготовке проекта к выносу в натуру, часть геодезических данных берется с плана или цифровой модели местности. Поэтому нужно знать точностные характеристики планов, к которым отнесем:
1. Точность топографического плана (точность изображения ситуации и рельефа).
2. Детальность и полнота отображения.
3. Точность определения расстояний.
4. Точность определения направлений и углов.
5. Точность определения площадей.
6. Точность определения высот, превышений и уклонов.
Точность изображения ситуации и рельефа.
Точность топографического плана характеризуется погрешностью планового положения точек ситуации относительно пунктов геодезической сети. Точность изображения рельефа характеризуется погрешностью горизонтали по высоте (СКП высот точек, лежащих на горизонтали). Инструкция по съемкам в крупных масштабах задает средние ошибки положения на плане предметов и контуров местности: с четкими очертаниями не более 0,5 мм, на открытой местности, 0,7 мм в горной и залесенной местности.
Средняя квадратическая погрешность связана со средней при нормальном законе распределения соотношением 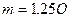 , в отношении планов соотношение составляет
, в отношении планов соотношение составляет 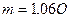 . То есть, средняя квадратическая погрешность примерно равна средней ошибке.
. То есть, средняя квадратическая погрешность примерно равна средней ошибке.
Для инженерно- топографических планов важной характеристикой является ошибка взаимного положения. Так предельная ошибка взаимного положения близлежащих зданий и сооружений на застроенной территории не должна превышать 0,4 мм.. Зная допустимую точность взаимного положения можно рассчитать масштаб съемки. Если положение четких контуров должно отображаться с точностью в 0,5 м то масштаб необходим 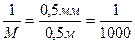 .
.
Проектирование строительных объектов выполняется не на оригиналах топографического плана, а на их копиях ( за исключением САПР, использующих ЦММ), Любая копия имеет ошибки больше , чем оригинал, копирование на кальку выполняется с СКП 0,1 мм, при копировании на ксероксе изменяется масштаб изображения и т.д.
Средние ошибки съемки рельефа относительно ближайших реперов не должны превышать ¼ высоты сечения рельефа при углах наклона менее 2 градусов. 1/3 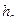 при углах наклона 2-6 градусов. На незастроенных, залесенных территориях допуски увеличиваются в 1,5 раза.
при углах наклона 2-6 градусов. На незастроенных, залесенных территориях допуски увеличиваются в 1,5 раза.
Таким образом СКП планового положения твердых контуров составляет 0,3-0,4 мм, фактическая СКП изображения рельефа по результатам многочисленных исследований составляет ¼-1/5 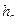 . Погрешность планового положения и съемки рельефа не зависят от метода съемки.
. Погрешность планового положения и съемки рельефа не зависят от метода съемки.
ДЕТАЛЬНОСТЬ- степень подобия изображения на плане контуров ситуации и рельефа. Связана с обобщением изображения, его генерализацией, как принято называть в картографии. Инструкции по съемкам в крупных масштабах требуют, чтобы ошибки за счет обобщения контуров не превышали 0,5 мм на плане. Для архитектурных деталей допускается ошибка обобщения не более 0,3 мм на плане. Детальность зависит от метода съемки, мензульные планы детальнее тахеометрических, наиболее детальны фотопланы.
ПОЛНОТА плана это степень его насыщенности объектами ситуации и элементами рельефа отображение которых необходимо и возможно при данном масштабе съемки. Полнота плана регламентируется мин размерами объектов, которые необходимо отображать при данном масштабе съемки и мин расстояниями между ними. Полнота плана является одним из главных масштабообразующих факторов при съемках застроенных территорий. Например при отображении густой сети коммуникаций , проложенных на различных уровнях, условные знаки будут читаться если расстояние между ними на плане будет не менее 1 мм, при густоте проложения коммуникаций через 0,5 м на местности масштаб съемки будет
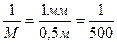 . По исследованиям профессора Неумывакина Ю.К полнота и детальность могут быть описаны информационными характеристиками (информационной емкостью т.е., содержанием единиц информации на единицу площади). На основе теории информации им предложен метод обоснования масштаба топографической съемки, на основе критерия избыточности информации.
. По исследованиям профессора Неумывакина Ю.К полнота и детальность могут быть описаны информационными характеристиками (информационной емкостью т.е., содержанием единиц информации на единицу площади). На основе теории информации им предложен метод обоснования масштаба топографической съемки, на основе критерия избыточности информации.
Точность расстояний, измеренных на плане.
На точность измеренного на плане расстояния влияют следующие факторы
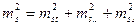 , (2.3)
, (2.3)
где 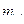 -ошибка расстояния, вызванная ошибками положения конечных точек.;
-ошибка расстояния, вызванная ошибками положения конечных точек.;
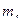 -погрешность, появляющаяся за счет способа (технологии) измерения расстояния;
-погрешность, появляющаяся за счет способа (технологии) измерения расстояния;
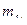 - погрешность возникающая за счет деформации бумаги(топографической основы).
- погрешность возникающая за счет деформации бумаги(топографической основы).
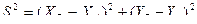 (2.4)
(2.4)
продифференцировав выражение по всем независимым переменными заменив дифференциалы квадратами средних квадратических погрешностей получим
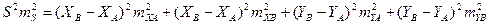 , (2.5)
, (2.5)
учитывая что 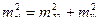 , получим
, получим
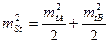 (2.6)
(2.6)
или
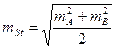 , (2.7)
, (2.7)
при равенстве погрешностей точек А и В
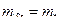 . (2.8)
. (2.8)
Это справедливо, если точки А и В сняты с разных станций, если с одной, то они коррелированны и нужно учитывать к-т корреляции
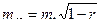 , (2.8)
, (2.8)
где коэффициент корреляции r = 0,4-0,6 (отношение погрешности опорной точки к погрешности контурной точки) при съемке точек А и В с одной станции. При съемке с разных станций корреляция отсутствует.
Точность измерения линии измерителем по масштабной линейке составляет 0,08 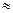 0,1 мм. на плане, то есть,
0,1 мм. на плане, то есть, 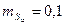 мм.
мм.
Погрешность вызванная деформаций топографической основы можно рассчитать по формуле
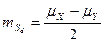 , (2.9)
, (2.9)
где 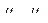 коэффициенты деформации бумаги по двум направлениям.
коэффициенты деформации бумаги по двум направлениям.
Для больших длин линий, расположенных на удалении от осевого меридиана необходимо учитывать поправку за искажение в проекции Гаусса- Крюгера, поправка вводится со знаком «-»
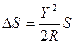 . (2.10)
. (2.10)
при У=300 км, 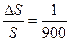 .
.
Точность направлений измеренных на плане.
Характеризуется средней квадратической погрешностью дирекционного угла линии
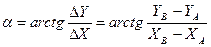 . (2.11)
. (2.11)
Продифференцировав это выражение и заменив дифференциалы квадратами средних квадратических. погрешностей получим
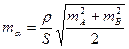 , (2.12)
, (2.12)
если погрешности точек А и В равны, то
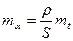 , (2.13)
, (2.13)
эта формула справедлива для независимых координат точек. Для зависимых необходимо учитывать коэффициент корреляции
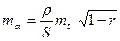 . (2.14)
. (2.14)
Точность углов на плане.
Погрешность угла можно описать выражением
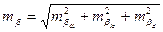 , (2.15)
, (2.15)
где
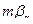 - погрешность угла за счет ошибки направления;
- погрешность угла за счет ошибки направления;
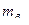 - погрешность за счет собственно измерения на плане;
- погрешность за счет собственно измерения на плане;
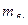 -погрешность за деформацию бумаги.
-погрешность за деформацию бумаги.
Если значение угла вычисляется по дирекционным углам направлений
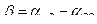 , (2.16)
, (2.16)
то
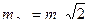 . (2.17)
. (2.17)
Если дирекционные углы вычисляются по координатам точек, то продифференцировав выражение
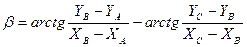 , (2.18)
, (2.18)
Затем, заменив дифференциалы квадратами средних квадратических погрешностей, получим
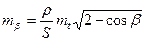 . (2.19)
. (2.19)
Средняя квадратическая погрешность измерения угла геодезическим транспортиром получена по результатам экспериментальных данных и составляет 5 минут.
Погрешность вызванную деформацией топографической основы можно рассчитать по формуле
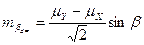 . (2.20)
. (2.20)
Точность площадей, измеренных на плане.
Площадь многоугольника на плане может быть получена по графическим координатам (измеренным на плане) поворотных точек
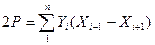 , (2.21)
, (2.21)
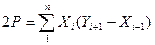 . (2.22)
. (2.22)
Дифференцируя это выражение по всем независимым переменным и перейдя от дифференциалов к квадратам средних квадратических погрешностей получим для фигуры близкой к квадрату
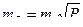 . (2.23)
. (2.23)
Для прямоугольника
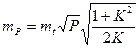 ., (2.24)
., (2.24)
где К- коэффициент вытянутости отношение длины к ширине.
При измерении площади разбивкой на геометрические фигуры погрешность площади можно рассчитать по известной формуле профессора А.В. Маслова
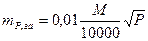 . (2.25)
. (2.25)
При использовании планиметра относительная ошибка площади составляет 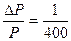 .
.
Для больших площадей необходимо учитывать искажение , вызванное применяемой картографической проекцией, особенно при удалении от осевого меридиана на расстояния более 300 км.
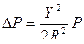 , (2.26)
, (2.26)
для У=300 км , относительная погрешность площади составит 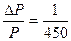 .
.
Точность определения высот точек, взятых с плана.
За точность изображения рельефа на плане принято считать погрешность положения горизонтали по высоте относительно пунктов геодезической высотной сети. Ошибку положения горизонтали по высоте можно рассчитать по общепринятой формуле Коппе
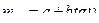 . (2.27)
. (2.27)
В этой формуле «а»- это группа факторов, вызывающая погрешность определения высоты относительно съемочной станции. Группа факторов «в» приводит к сдвигу горизонтали в плане относительно съемочной станции, вызывая дополнительную погрешность по высоте, величина которой зависит также от угла наклона местности.
Имеется ряд эмпирических формул различных авторов для получения погрешности положения горизонтали, например формула профессора Видуева
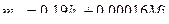 , (2.28)
, (2.28)
где 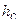 - высота сечения рельефа,
- высота сечения рельефа, 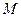 - знаменатель масштаба,
- знаменатель масштаба,  - уклон.
- уклон.
Масштаб, высота сечения рельефа и сложность снимаемого рельефа между собой всегда увязываются.
Точность определения превышений можно оценить на основе формулы
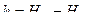
 , (2.29)
, (2.29)
дифференцируя это выражение по всем независимым переменным и заменив дифференциалы квадратами ср. кв погрешностей получим
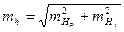 , (2.30)
, (2.30)
при 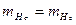 получим
получим
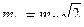 , (2.31)
, (2.31)
для коррелированных горизонталей
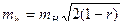 . (2.32)
. (2.32)
В научной литературе рекомендуется вычислять коэффициент корреляции по формуле
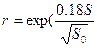 , (2.33)
, (2.33)
где 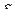 - расстояние между точками А и В,
- расстояние между точками А и В, 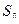 - расстояние между пикетами по инструкции.
- расстояние между пикетами по инструкции.
Точность определения уклонов на плане.
Уклон это тангенс угла наклона, его можно получить через превышение 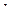 и горизонтальное проложение
и горизонтальное проложение 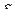 , измеренные на плане
, измеренные на плане
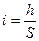 . (2.34)
. (2.34)
Прологарифмировав выражение (2.34) получим
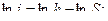 (2.35)
(2.35)
затем продифференцируем выражение (2.35) по всем независимым переменным
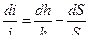 . (2.36)
. (2.36)
Заменив дифференциалы квадратами средних квадратических погрешностей, получим
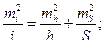 (2.37)
(2.37)
учитывая, что относительная ошибка превышения намного больше относительной ошибки расстояния 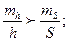 получим , что
получим , что
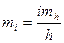 , (2.38)
, (2.38)
подставив значение уклона получим
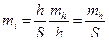 . (2.39)
. (2.39)
С учетом выражения (2.31) получим погрешность уклона
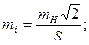 (2.40)
(2.40)
для коррелированных горизонталей формула (2.40) примет вид
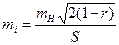 . (2.41)
. (2.41)
2.8 Способы определения объемов земляных работ
Дата: 2018-12-21, просмотров: 369.