В общем случае порядок обработки результатов прямых измерений следующий (предполагается, что систематических ошибок нет).
Случай 1. Число измерений меньше пяти.
1) По формуле (6) находится средний результат x, определяемый как среднее арифметическое от результатов всех измерений, т.е.
.
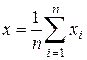2) По формуле (12) вычисляются абсолютные погрешности отдельных измерений
.
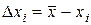3) По формуле (14) определяется средняя абсолютная погрешность
.
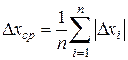4) По формуле (15) вычисляют среднюю относительную погрешность результата измерений
.
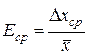5) Записывают окончательный результат по следующей форме:
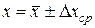, при 
.
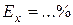Случай 2. Число измерений свыше пяти.
1) По формуле (6) находится средний результат
.
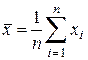2) По формуле (12) определяются абсолютные погрешности отдельных измерений
.
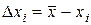3) По формуле (7) вычисляется средняя квадратическая погрешность единичного измерения
.
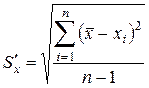4) Вычисляется среднее квадратическое отклонение для среднего значения измеряемой величины по формуле (9).
.
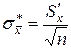5) Записывается окончательный результат по следующей форме
.
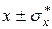Иногда случайные погрешности измерений могут оказаться меньше той величины, которую в состоянии зарегистрировать измерительный прибор (инструмент). В этом случае при любом числе измерений получается один и тот же результат. В подобных случаях в качестве средней абсолютной погрешности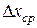 
принимают половину цены деления шкалы прибора (инструмента). Эту величину иногда называют предельной или приборной погрешностью и обозначают 
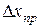(для нониусных приборов и секундомера 
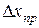равна точности прибора).
Оценка достоверности результатов измерений
В любом эксперименте число измерений физической величины всегда по тем или иным причинам ограничено. В связи с этим может быть поставлена задача оценить достоверность полученного результата. Иными словами, определить, с какой вероятностью можно утверждать, что допущенная при этом ошибка не превосходит наперед заданную величину ε. Упомянутую вероятность принято называть доверительной вероятностью. Обозначим её буквой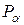 
.
Может быть поставлена и обратная задача: определить границы интервала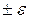 
, чтобы с заданной вероятностью 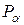можно было утверждать, что истинное значение измерений величины 
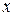не выйдет за пределы указанного, так называемого доверительного интервала.
Доверительный интервал характеризует точность полученного результата, а доверительная вероятность — его надёжность. Методы решения этих двух групп задач имеются и особенно подробно разработаны для случая, когда погрешности измерений распределены по нормальному закону. Теория вероятностей даёт также методы для определения числа опытов (повторных измерений), при которых обеспечивается заданная точность и надёжность ожидаемого результата. В данной работе эти методы не рассматриваются (ограничимся только их упоминанием), так как при выполнении лабораторных работ подобные задачи обычно не ставятся.
Особый интерес, однако, представляет случай оценки достоверности результата измерений физических величин при весьма малом числе повторных измерений. Например,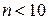 
. Это именно тот случай, с которым мы часто встречаемся при выполнении лабораторных работ по физике. При решении указанного рода задач рекомендуется использовать метод, в основе которого лежит распределение (закон) Стьюдента.
Для удобства практического применения рассматриваемого метода имеются таблицы, с помощью которых можно определить доверительный интервал 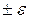, соответствующий заданной доверительной вероятности 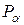или решить обратную задачу.
Ниже приведены те части упомянутых таблиц, которые могут потребоваться при оценке результатов измерений на лабораторных занятиях.
Пусть, например, произведено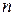 
равноточных (в одинаковых условиях) измерений некоторой физической величины 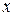и вычислено её среднее значение 
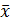. Требуется найти доверительный интервал 
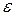, соответствующий заданной доверительной вероятности 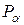. Задача в общем виде решается так.
По формуле с учётом (7) вычисляют
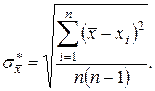
Затем для заданных значений n и 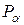находят по таблице (табл. 2) величину 
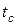. Искомое значение вычисляется на основе формулы
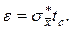(16)
При решении обратной задачи вначале вычисляют по формуле (16) параметр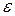 
. Искомое значение доверительной вероятности 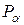берётся из таблицы (табл. 3) для заданного числа 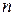и вычисленного параметра .
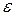Таблица 2. Значение параметра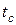 
при заданных числе опытов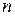 
и доверительной вероятности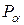 
|
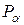n
| 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,95 | 0.98 | 0,99 | 0.995 | 0,999 |
| 2 | 1,000 | 1,376 | 1,963 | 3,08 | 6,31 | 12,71 | 31,8 | 63,7 | 127,3 | 637,2 |
| 3 | 0,816 | 1,061 | 1,336 | 1,886 | 2,91 | 4,30 | 6,96 | 9,92 | 14,1 | 31,6 |
| 4 | 0,765 | 0,978 | 1,250 | 1,638 | 2,35 | 3,18 | 4,54 | 5,84 | 7,5 | 12,94 |
| 5 | 0,741 | 0,941 | 1,190 | 1,533 | 2,13 | 2,77 | 3,75 | 4,60 | 5,6 | 8,61 |
| 6 | 0,727 | 0,920 | 1,156 | 1,476 | 2,02 | 2,57 | 3,36 | 4,03 | 4,77 | 6,86 |
| 7 | 0.718 | 0,906 | 1,134 | 1,440 | 1,943 | 2,45 | 3,14 | 3,71 | 4,32 | 5,96 |
| 8 | 0,711 | 0,896 | 1,119 | 1,415 | 1,895 | 2,36 | 3,00 | 3,50 | 4,03 | 5,40 |
| 9 | 0,706 | 0,889 | 1,108 | 1,397 | 1,860 | 2,31 | 2,90 | 3,36 | 3,83 | 5,04 |
| 10 | 0,703 | 0,883 | 1,110 | 1,383 | 1,833 | 2,26 | 2,82 | 3,25 | 3,69 | 4,78 |
Таблица 3 Значение доверительной вероятности 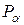при заданном числе опытов n и параметре ε
|
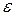n
| 2 | 2,5 | 3 | 3,5 |
| 2 | 0,705 | 0,758 | 0,795 | 0,823 |
| 3 | 0,816 | 0,870 | 0,905 | 0,928 |
| 4 | 0,861 | 0,912 | 0,942 | 0,961 |
| 5 | 0,884 | 0,933 | 0,960 | 0,975 |
| б | 0,898 | 0,946 | 0,970 | 0,983 |
| 7 | 0,908 | 0,953 | 0,976 | 0,987 |
| 8 | 0,914 | 0,959 | 0,980 | 0,990 |
| 9 | 0,919 | 0.963 | 0,983 | 0,992 |
| 10 | 0,923 | 0,969 | 0,985 | 0,993 |
Обработка результатов косвенных измерений
Очень редко содержание лабораторной работы или научного эксперимента сводится к получению результата прямого измерения. Большей частью искомая величина является функцией нескольких других величин.
Задача обработки опытов при косвенных измерениях заключается в том, чтобы на основании результатов прямых измерений некоторых величин (аргументов), связанных с искомой величиной определённой функциональной зависимостью, вычислить наиболее вероятное значение искомой величины и оценить погрешность косвенных измерений.
Существует несколько способов обработки косвенных измерений. Рассмотрим следующие два способа.
Пусть по методу косвенных измерений определяется некоторая физическая величина.
Результаты прямых измерений ее аргументов х, у, z приведены в табл. 4.
Таблица 4
| Номер опыта | x | y | z | … |
| 1 |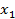 
| 
| 
| … |
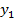
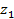
| 2 |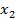 
| 
| 
| … |
| … | … | … | … | … |
| … | … | … | … | … |
| … | … | … | … | … |
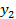
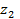
| n |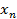 
| 
| 
| … |
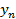
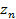
Первый способ обработки результатов заключается в следующем. С помощью расчетной (17) формулы вычисляют искомую величину по результатам каждого опыта
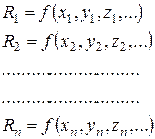(17)
Далее обычным методом можно вычислить её наивероятнейшее — значение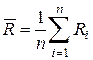 
, а также среднюю погрешность, используя формулы (9) или (14).
Описанный способ обработки результатов применим, в принципе, во всех без исключения случаях косвенных измерений. Однако наиболее целесообразно применять его тогда, когда число повторных измерений аргументов небольшое, а расчётная формула косвенно измеряемой величины сравнительно проста.
При втором способе обработки результатов опытов вначале вычисляют, используя результаты прямых измерений (табл. 4), средние арифметические значения каждого из аргументов, а также погрешности их измерения. Подставив ,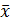 
, 
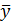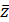,... в расчетную формулу (17), определяют наиболее вероятное значение измеряемой величины
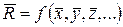(17*)
и выполняют оценку результатов косвенных измерений величины.
Второй способ обработки результатов применим лишь к таким косвенным измерениям, при которых истинные значения аргументов от измерения к измерению остаются постоянными.
Погрешности косвенных измерений величины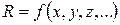 
зависят от погрешностей прямых измерений её аргументов.
Если систематические погрешности измерений аргументов исключены, а случайные погрешности измерения этих аргументов не зависят друг от друга (некореллированы), то ошибка косвенного измерения величины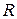 
определяется в общем случае по формуле:
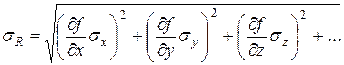, (18)
где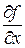 
, 
, 
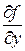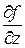— частные производные; 
, 
, 
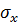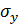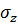– средние квадратические погрешности измерения аргументов , 
, 
, …
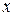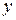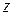Относительная погрешность вычисляется по формуле
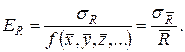(19)
В ряде случаев значительно проще (с точки зрения обработки результатов измерений) вычислить вначале относительную погрешность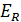 
, а затем, используя формулу (19), абсолютную погрешность результата косвенного измерения:
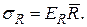(20)
При этом формулы для вычисления относительной погрешности результата составляются в каждом отдельном случае в зависимости от того, каким образом искомая величина связана своими аргументами. Имеются таблицы формул относительных погрешностей для наиболее часто встречающихся видов (структуры) расчётных формул (табл. 5).
Таблица 5 Определение относительной погрешности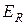 
, допускаемой при вычислении приближенной величины 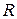, зависящей от приближённой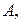 
.
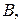
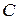| Характер связи главной величины с приближенными величинами | Формула для определения относительной погрешности |
Сумма: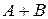 
| 
|
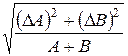
Разность: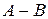 
| 
|
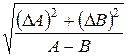
Произведение: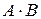 
| 
|
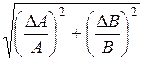
Частное: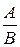 
| 
|
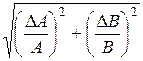
Степень: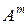 
| 
|
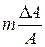
Изучение нониусов
Измерение длины производится с помощью масштабных линеек. Для увеличения точности измерения пользуются вспомогательными подвижными шкалами — нониусами. Например, если масштабная линейка разделена на миллиметры, т. е. цена одного деления линейки 1 мм, то с помощью нониуса можно повысить точность измерении по ней до одной десятой или более мм.
Нониусы бывают линейными и круговыми. Разберем устройство линейного нониуса. На нониусе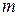 
делений, которые в сумме равны 1 делению основной шкалы. Если 
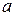— цена деления нониуса, 
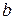— цена деления масштабной линейки, то можно написать
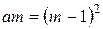. (21)
Отношение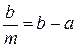 
называется точностью нониуса. Если, например, b=1 мм, a m=10, то точность нониуса 0,1 мм.
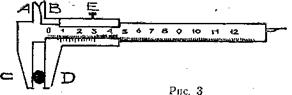
Из рис. 3 видно, что искомая длина тела равна:
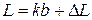, (22)
где k— целое число делений масштабной линейки;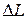 
— число делений миллиметра, которое необходимо определить с помощью нониуса.
Обозначим через п — число делений нониуса, совпадающее с любым делением масштабной линейки. Следовательно:
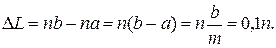
Таким образом, длина измеряемого тела равна целому числу k мм масштабной линейки плюс десятые доли числа миллиметров. Аналогично устроены и круговые нониусы.
Нижняя шкала наиболее распространенного микрометра представляет собой обычную миллиметровую шкалу (рис. 4).
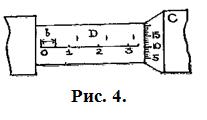Риски верхней шкалы сдвинуты по отношению к рискам нижней шкалы на 0,5 мм. При повороте микрометрического винта на 1 оборот барабан 
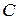вместе со всем винтом передвигается на 0,5 мм, открывая или закрывая поочередно риски то верхней, то нижней шкалы. Шкала на барабане содержит 50 делений, таким образом, точность микрометра 
.
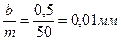При отсчёте по микрометру необходимо учитывать целое число рисок верхней и нижней шкалы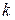 
(умножая это число на 0,5 мм) и номер деления барабана n, который в момент отсчёта совпадает с осью шкалы стебля D, умножая его на точность микрометра. Иными словами, числовое значение L длины измеряемого микрометром предмета находят по формуле:
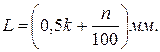(23)
Для того чтобы измерить длину предмета или диаметр отверстия штангенциркулем (рис. 3), следует поместить предмет между неподвижной и "подвижной ножкам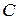и и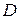 
или развести выступы 
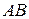по диаметру внутри измеряемого отверстия. Движение перемещающегося устройства штангенциркуля проводится без сильного нажима. Вычисление длины производят по формуле (23), снимая отсчёт по основной шкале и нониусу.
В микрометре для измерения длины предмет зажимают между упором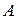 
и микрометрическим винтом 
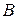(рис. 5), вращая последний только с помощью головки 
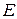, до срабатывания трещотки.
Длину измеряемого предмета находят с помощью формулы (23), используя показания линейной шкалы 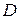и шкалы барабана .
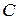Порядок выполнения работы
Задание 1. Измерение диаметра проволоки с помощью микрометра.
1. Измерьте не менее 7 раз диаметр проволоки в разных местах. Результаты занести в табл. 6.
Таблица 6
| Номер измерения |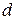 
| 
| 
|
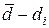
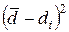
| 1 | |||
| … | |||
| … | |||
| … | |||
| 7 |
2. Определите границу допускаемой абсолютной ошибки микрометра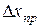 
(приборная ошибка).
3. Вычислите среднее значение диаметра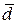 
, среднеквадратическое отклонение 
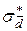по формулам методики обработки результатов прямых измерений (случай 2).
4. Определите границу доверительного интервала для заданной доверительной вероятности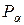 
(задается преподавателем) и числа опытов n.
Сравните приборную погрешность с доверительным интервалом. В окончательный результат запишите большее значение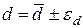 
.
Задание 2. Определение объема цилиндра с помощью микрометра и штангенциркуля.
1. Измерьте не менее 7 раз диаметр цилиндра микрометром, а высоту штангенциркулем. Результаты измерений запишите в таблицу (табл. 7).
Таблица 7
| Номер измерения |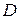
| 
| 
| 
| 
|
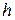
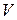
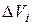
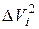
| 1 | |||||
| … | |||||
| … | |||||
| … | |||||
| 7 |
2. Определите объем цилиндра для каждого отдельного измерения
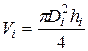(24)
3. Определите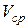 
и 
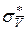по формулам методики обработки результатов прямых измерений (случай 2).
4. Определите доверительный интервал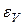 
для косвенно измеряемой величины по заданной доверительной вероятности 
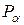и числу опытов n.
.
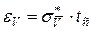5. Оцените границу абсолютной допускаемой ошибки микрометра и штангенциркуля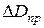 
и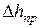 
.
6. Вычислите относительную приборную ошибку для объёма цилиндра по формуле
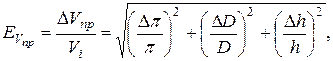(25)
где 
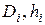и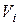 
берутся из таблицы результатов опытов (табл. 7) и соответствуют случаю, когда 
.
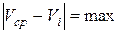7. Вычислите абсолютную приборную погрешность объема
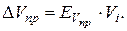(26)
8. Сравните абсолютную приборную погрешность и доверительный интервал. Если они одного порядка, то ошибка измерения объема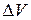 
вычисляется по формуле:
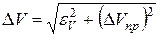. (27)
Если они отличаются хотя бы на порядок, то берется наибольшая ошибка.
9. Окончательный результат запишите в виде:
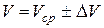. (28)
Примечание. При расчёте приборной ошибки по формуле (25) одновременно учитывается и ошибка, обусловленная округлением чисел, так как они подчиняются одному и тому же закону распределения.
Контрольные вопросы
1. Опишите известные Вам виды измерений.
2. Дайте определение систематической и случайной ошибкам. В чём состоит их основное различие?
3. Какие виды ошибок подчиняются равномерному распределению?
4. Опишите порядок обработки результатов прямых (косвенных) измерений.
5. Почему при измерении объема цилиндра Вам рекомендовалось диаметр измерять микрометром, а высоту — штангенциркулем?
6. Относительная ошибка измерения массы тела составляет 1%, а его скорости—2%. С какой относительной ошибкой можно по таким данным вычислить кинетическую энергию тела?
Лабораторная работа №2
Дата: 2018-12-21, просмотров: 438.
