1. Орлов А.И. Эконометрика: Учебник. - М.: Изд-во «Экзамен», 2004. - 576 с
4. Тихомиров Н.П. Дорохина Е Эконометрика: Учебник. – М.: Изд-во «Экзамен», 2007. – 512 с.
3. Доугерти К. Введение в эконометрику: Учебник. – М.: Изд-во Инфра-М, 2006. – 432 с. – (Серия «Университетский учебник»).
4. Колемаев В.А. Эконометрика: Учебник. – М.: Изд-во Инфра-М, 2007. – 160 с.
5. Магус Я. Р., Катышев П.К., Пересецкий А. А. Эконометрика. Начальный курс/ Учебник – 7-е изд. перераб. и доп. – М.: Дело. 2005. –504 с.
6. Луговская Л. В. Эконометрика в вопросах и ответах: учеб. пособие. – М.: ТК Велби, изд-во «Проспект», 2005. – 208 с.
7. Суслов В.И., Ибрагимов Н.М., Талышева Л.П., Цыплаков А.А. Эконометрия: Учебное пособие. - Новосибирск: Изд-во СО РАН, 2005. - 744 с.
8. Варюхин А.М. , Панкина О.Ю. , Яковлева А.В. Эконометрика: Пособие для сдачи экзамена. – М.: Изд-во Юрайт, 2005. - 191 с.
9. Басовский Л.Е. Эконометрика: Учебное пособие. – М.: Изд-во РИОР, 2005. – 48 с.
10. Герасимов А.Н. , Гладилин А.В. , Громова Е.И. Эконометрика: Учебное пособие. – М.: Изд-во КноРус, 2008. – 232 с.
11. Просветов Г. И. Эконометрика. Задачи и решения: Учебно-методическое пособие – 4 изд. – М.: Изд-во РДЛ, 2007. – 192 с.
Планы практических занятий
| № | Тема | Содержание | Часы | Лит. источник |
| 1 | 2 | 3 | 4 | 5 |
| 1 | Тема 2.Построение моделей парной регрессии методом наименьших квадратов. | Нахождение уравнений парной регрессии. Вычисление коэффициента корреляции между переменными Х и У. Оценка параметров парной регрессионной модели. Построение доверительных интервалов для функции регрессии и ее параметров. Оценка значимости коэффициентов регрессии. Вычисление коэффициента детерминации. Проверка значимости полученного уравнения регрессии. Построение моделей множественной регрессии . | 3 | [1], [2] |
| 2 | Тема 3.Фиктивные переменные. Критерий Чоу. | Построение линейной регрессионной модели с учетом фиктивных переменных и без учета их. Проверка значимости построенных моделей и сравнение их. | 2 | [1], [2] |
| 3 | Тема 4. Мультиколлинеарность. Тесты на наличие и устранения мультиколлинеарности для оценок параметров регрессионной модели. | Построение матрицы парной корреляции между факторами (х i, х j) и (y, x i) . Анализ полученной матрицы и в случае обнаружения мультиколлинеарности использование процедуры пошагового отбора наиболее информативных переменных. | 2 | [1], [2] |
| 4 | Тема 5. Гомоскедастичность и гетероскедастичность. Тесты на наличие и устранения гетероскедастичности. | Применение теста Голдфелда - Квандта с целью обнаружения гетероскедастичности и в случае наличия ее использование метода взвешенного метода наименьших квадратов. | 2 | [1], [2] |
| 1 | 2 | 3 | 4 | 5 |
| 5 | Тема 7. Временные ряды. Стационарные и нестационарные временные ряды. Автокорреляционная функция. Аналитическое выравнивание временного ряда. | Нахождение среднего значения, среднего квадратического отклонения для временного ряда, коэффициентов автокорреляции для различных лагов и частного коэффициента автокорреляции 1-го порядка. Нахождение уравнения неслучайной составляющей тренда для временного ряда. Проведения сглаживания временного ряда методом скользящих средних. Построение точечной интервальной оценки прогноза средней и индивидуального значений временного ряда. | 2 | [1], [2] |
| 6 | Тема 7. Тесты на наличие автокорреляции и ее устранение. | Использование теста Дарбина-Уотсона для обнаружения автокорреляции и ее устранения. | 2 | [1], [2] |
| 7 | Тема 10. Статистические уравнения зависимостей (однофакторные и многофакторные). | Расчет параметров однофакторных и многофакторных уравнений зависимости. Вычисление коэффициента и индекса корреляции. Вычисление коэффициента устойчивости связи для оценки достоверности эконометрических расчетов. Нормативные расчеты микроэкономических показателей хозяйственной деятельности. Моделирование динамики и прогнозирование экономических процессов. | 2 | [1], [2] |
| 8 | Контрольная. работа | 2 | ||
| Итого | 17 | |||
Глоссарий
1. Уравнение Y t = b 0 + b 1 X t + e t , t = 1,….,n,
где
X t -неслучайная (детерминированная) величина, Y t , b 0 и b 1 – неизвестные параметры, e t -случайные величины, называется линейным регрессионным уравнением.
Y t называется объясняемой ( зависимой) переменной, а X t -объясняющей (независимой) переменной или регрессором
2. Основные гипотезы:
1. Y t = b 0 + b 1 X t + e t , t = 1,….,n, - спецификация модели.
2. X t - детерминированная величина;
3. e i - случайная величина, удовлетворяющая следующим предпосылкам
3а). Ee t = 0, ( ЕY t =b 0 + b 1 X t ), E (e t2) = V(e t) = s 2 , (V(Y t ) = s 2) - не зависит от t.
3б). E(e t e s) = 0 (Cov (Y t , Y s)=0), t ¹ s - некоррелированность ошибок для разных наблюдений.
Часто добавляется условие:
3в). e t ~ N( 0, s 2), т.е. e t - нормально распределенная случайная величина со средним 0 и дисперсией s 2 .
Условие независимости дисперсии ошибки от номера наблюдений E (e t2) = s 2, t = 1,….,n , называется гомоскедастичностью ( а); случай, когда условие гомоскедастичности не выполняется , называется гетероскедастичностью (б).
Теорема Гаусса - Маркова.
Для модели 1 -3ab:
оценки b 0, b 1 параметров регрессии, полученные по методу наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещенных оценок s 2 .
3. Коэффициентом детерминации R 2 или долей объясненной дисперсии называется
R 2 = 1 -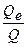 
= 
.
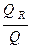Q - вся дисперсия , Q e - остаточная дисперсия, Q R - объясненная часть всей дисперсии.
4.Классическая нормальная линейная модель множественной регрессии.
Модель множественной регрессии:
y i = b 0 + b 1 x i1 + b 2 x i3 + b p x i p + e i i = 1,2, … n;
где х tp - значения регрессора х p в наблюдении t.
Основные гипотезы, лежащие в основе модели множественной регрессии, являются естественным обобщением модели парной регрессии:
1. y i = b 0 + b 1 x i1 + b 2 x i3 + b p x i p + e i i = 1,2, … n;
- спецификация модели.
2. x i 1, x i 2,…. x i p -детерминированные величины. Векторы х s = (x 1s, …. x n s)', s = 1,….p линейно независимы в R n.
3. e i - случайная величина, удовлетворяющая следующим предпосылкам:
3a) Е(e i ) = 0; D (e i ) = s 2 для любого i ;
3б) e i и e j не коррелированы: Е(e i, e j) = 0 при i ¹ j ; выводится из условия некоррелированности Cov (e i , e j) = 0; (Cov (e i , e j) = Е[(e i - 0) ((e j - 0)]) = Е(e i, e j) = 0).
Часто добавляется условие:
3в). e t ~ N(0, s 2), т.е. e t - нормально распределенная случайная величина со средним 0 и дисперсией s 2.
В этом случае модель называется нормальной линейной регрессионной.
Все эти условия удобно записать в матричной форме:
У = Х × b + e или
у i = b 0 +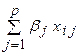 
+ e i , i = 1,2,….n.
где У = (у 1,…у n) ' - вектор значений зависимой переменной ;
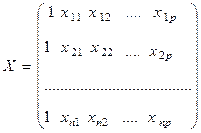- матрица значений объясняющих переменных, в которую дополнительно введен столбец, все элементы которого равны 1, т.е. условно полагается, что модели (МР1) свободный член b 0 умножается на фиктивную переменную х i 0, принимающую значение 1 для всех i :
х i 0 =1 (i = 1,2,….n);
b = (b 0 , b 1 , …… b p)' - вектор параметров размера (р + 1); e = (e 1,e 2,…. e n) - вектор возмущений (случайных ошибок) размера n.
Теорема Гаусса - Маркова.
Предположим, что:
1. у = Х b + e ;
2. Х - детерминированная n ´ (p+1) матрица, имеет максимальный ранг (p+1) ;
3. Е(e ) = 0; Е(e e ') = s 2 1 n.
4. e - нормально распределенный случайный вектор e ~ N(0, s 21 n);
5. r (X) = p + 1 < n
Тогда при выполнении предпосылок (1-3, 5) оценка МНК b = (X ' X) - 1 X ' y является наиболее эффективной ( в смысле наименьшей дисперсии) оценкой в классе линейных (по у ) несмещенных оценок.
5. Ковариационная матрица и ее выборочная оценка.
Вариации оценок параметров будут определять точность уравнения множественной регрессии. Для их вычисления используют ковариационную матрицу вектора оценок параметров å b .
å b =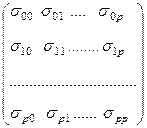 
,
где s ij 2 - ковариации (корреляционные моменты) оценок параметров b i и b j .
s ij 2 = Е[ (b i - Е(b i))(b j - Е(b j))]. (МР7)
Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных.
Оценка дисперсии ошибок s 2. Распределение s 2.
S 2 =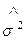 
= 
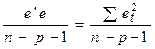
является несмещенной оценкой дисперсии ошибок (возмущений) s 2, т.е. Еs 2 = s 2.
6. Оценка значимости коэффициентов регрессии b j .
Значимость коэффициентов регрессии b j можно проверить, если учесть, что статистика (b j - b j0 )/ s b j имеет t - распределение Стьюдента с к = n - p - 1 степенями свободы. Поэтому b j значимо отличается от нуля ( т.е. гипотеза Н 0 о равенстве параметра b j нулю Н 0 : b j0 = 0, отвергается) на уровне значимости a , если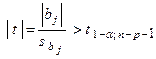 
, где t 1 - a; n - p -1 - табличное значение t - критерия Стьюдента, определенное на уровне значимости a при числе степеней свободы к = n - p - 1.
7. Доверительный интервал для параметра b j есть
b j - t 1 - a; n - p -1 s b j £ b j £ b j + t 1 - a; n - p -1 s b
8. Доверительный интервал для функции регрессии или для условного математического ожидания зависимой переменной Е х(У):
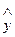- t 1 - a; k 
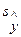< Е(Y) < 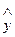+ t 1 - a; k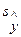
где 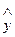- групповая средняя, определяемая по уравнению регрессии,
= 
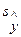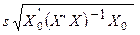- ее стандартная ошибка.
9. Доверительный интервал для индивидуальных значений зависимой переменной у *0 примет вид:
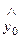- t 1 - a; n - p -1 
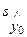< у *0 < 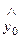+ t 1 - a; n - p - 1 ,
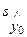где =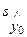 
.
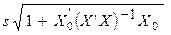10. Доверительный интервал для параметра s 2 в множественной регрессии:
.
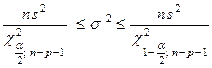11.Оценка значимости уравнения регрессии.
Проверить значимость уравнения регрессии - значит установить, соответствует ли математическая модель, выражающая зависимость между переменными и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной.
При отсутствии линейной зависимости между зависимой переменной и объясняющей переменными несмещенные оценки дисперсий s2R = QR/(m - 1) и s2e = Qe/(n - m) имеют c 2 -распределение с соответственно к = m - 1 и к = n - m степенями свободы, а их отношение - F -распределение с теми же степенями свободы. Поэтому уравнение регрессии значимо на уровне a , если фактически наблюдаемое значение статистики
F =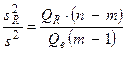 
> Fa; k1;k2 ,
где Fa; k1;k2 - табличное значение F - критерия Фишера - Снедекера, определенное на уровне значимости a при к 1 = m - 1 и к 2 = n - m степенях свободы.
Значение F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.
12.Оценка значимости коэффициента корреляции при отсутствии корреляционной связи статистика t =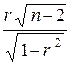 
имеет распределение Стьюдента с (n - 2) степенями свободы. Коэффициент корреляции r значим на уровне a (т.е. гипотеза Н 0 о равенстве генерального коэффициента корреляции r = 0 отвергается ), если
½ t½ =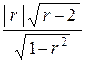 
> t 1 - a; n - 2 .
13. Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных.
14. Автокорреляции ошибок, если E(e t e s) = r ¹ 0,
15.Стандартизированные коэффициенты регрессии b'j и коэффициенты эластичности Е j (j = 1,….p):
b'j =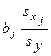 
;
E j =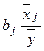 
.
Стандартизированный коэффициент регрессии b'j показывает, на сколько величин s y изменится в среднем зависимая переменная У при увеличении только j -ой объясняющей переменной на s x j , а коэффициент эластичности Е j - на сколько процентов (от средней) изменится в среднем У при увеличении только Х j на 1 %.
16. Временным рядом (динамическим рядом или рядом динамики) в экономике называется последовательность наблюдений некоторого признака (случайной величины) У в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда, которые обозначаются у t (t = 1,2,….n), где n - число уровней.
В общем виде при исследовании экономического временного ряда у t выделяются несколько составляющих:
у t = u t + n t + c t + e t t = 1,2,….n,
где u t - тренд,
n t - сезонная компонента,
c t - циклическая компонента,
e t - случайная компонента,
u t, n t , c t - закономерные, неслучайные составляющие.
17. Стационарные временные ряды.
Временной ряд у t (t=1,2,…,n) называется строго стационарным, если совместное распределение вероятностей n наблюдений у 1, у 2,…..уn такое же, как и n наблюдений у 1 + t , у 2 + t ,…у n + t при любых n, t и t , т.е. свойства строго стационарных рядов у t (закон распределения и его числовые характеристики) не зависят от момента t .
18. Степень тесноты связи между последовательностями наблюдений временного ряда у 1, у 2,…у n и у 1 + t , у 2 + t ,….у n + t (сдвинутых относительно друг друга на t единиц, т.е. с лагом t ) может быть определена с помощью коэффициента корреляции
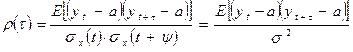
так как Е(у t) = Е(у t + t) = a, s y(t) = s y(t + t) = s.
Так как коэффициент r(t) измеряет корреляцию между членами одного и того же ряда, его называют коэффициентом автокорреляции, а зависимость r(t) - автокорреляционной функцией. В силу стационарности временного ряда у t автокорреляционная функция r(t) зависит от лага t , причем r( - t) = r(t), т.е. при r(t) можно ограничиться рассмотрением только положительных значений t.
19. Статистической оценкой r ( t ) является выборочный коэффициент автокорреляции r(t) , определяемый по формуле
r(t) =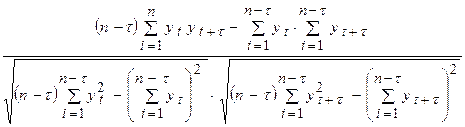 
.
Функцию r(t) называют выборочной автокорреляционной функцией, а ее график - коррелограммой.
Контрольные вопросы к итоговой аттестации
1. Предмет, задачи, критерии и принципы эконометрики.
2.Типы моделей, используемые для анализа и прогноза экономических процессов.
3.Метод наименьших квадратов.
4.Основные эконометрические методы.
5. Построение модели парной регрессии.
6. Теорема Гаусса - Маркова.
7.Построение модели множественной регрессии.
8.Оценка коэффициентов линейной регрессии.
9.Коэффициент корреляции.
10. Коэффициент детерминации.
11.Мультиколлинеарность. Тесты на наличие мультиколлинеарности.
12.Тесты на устранение мультиколлинеарности.
13. Гомогедастичность и гетероскедастичность. Тесты на наличие гетероскедастичности
13. Тесты на устранение гетероскедастичности.
14.Фиктивные переменные. Критерий Чоу.
15.Временные ряды. Стационарные и нестационарные временные ряды.
16.Автокорреляция остатков временного ряда. Тесты на наличие автокорреляции.
17. Устранение автокорреляции.
18. Понятие об авторегрессионных моделях.
19. Модели скользящей средней.
20.Метод инструментальных переменных.
21.Оценивание моделей с распределенными лагами.
22. Системы одновременных уравнений.
23. Двухшаговый метод наименьших квадратов.
24. Трехшаговый метод наименьших квадратов.
Дата: 2018-12-21, просмотров: 325.
