Цели и задачи курса
Целью изучения дисциплины «Эконометрика» является развитие математического мышления и навыков использования математических методов и основ математического моделирования в макроэкономике
Дисциплина «Эконометрика» предназначена для выработки у студентов умения проводить строгий логический и количественный анализ процессов в области макроэкономики с построением моделей их описания для прогнозирования явлений;
В результате изучения дисциплины студент должен знать и уметь использовать:
§ основы теории вероятностей и математической статистики;
§ математические методы при изучении социально-экономических процессов в различных областях экономики;
§ математические методы и модели при исследовании и решении задач управления экономическими системами с использованием различных средств информационного обеспечения.
Для выработки у современных специалистов по финансам и кредиту необходимой научной культуры программа по «Эконометрике» предусматривает реализацию следующей основной задачи: ориентация на обучение и выработку у студентов навыков и умения строить и использовать эконометрические модели для описания и прогнозирования различных процессов в области экономики.
Связь с другими дисциплинами.
Курс базируется на дисциплинах "Теория вероятностей" и "Математическая статистика", "Многомерные статистические методы", "Статистический анализ нечисловой информации". С другой стороны он является основой для дисциплины "Эконометрическое моделирование".
Виды занятий и методика обучения
Курс эконометрики изучается в одном семестре в форме лекций и практических занятий. Предусмотрена самостоятельная подготовка студентов.
На лекциях излагается содержание дисциплины, проводится анализ основных понятий и методов. Чтение лекций сопровождается рассмотрением примеров, соответствующих основным положениям лекций и должно быть логичным, наглядным, ориентированным на последующие приложения излагаемого материала в других дисциплинах.
На практических занятиях студент овладевает основными методами и приемами решения задач, а также получает разъяснение теоретических положений курса. При подборе задач следует стремится выбрать те из них, которые возникают в соответствующих приложениях и в процессе решения задач давать интерпретацию и трактовку.
При проведении практических занятий со студентами рекомендуется обращать особое внимание:
§ на развитие аналитических и вычислительных способностей и формирование соответствующих навыков;
§ на привитие навыков составления и анализа математических моделей простых реальных задач;
§ на выработку умения решать прикладные задачи, связанные с будущей специальностью студента, требующие отбора данных и предварительного вывода аналитических зависимостей;
§ методам контроля правильности решения задач.
Самостоятельная работа студентов является важной формой усвоения курса математики. Она должна состоять из непрерывной работы студента по выполнению текущих заданий и типовых расчетов. Типовой расчет является индивидуальным заданием по разделам (темам), изучаемым в семестре. Он состоит из теоретических вопросов (8 - 10), задач и примеров (8 - 10). Теоретические вопросы и упражнения являются общими для всех студентов, задачи и примеры индивидуальны.
Формы контроля
Результативность самостоятельной работы студентов обеспечивается эффективной системой контроля, включающей в себя вопросы по содержанию лекций и проверку выполнения текущих заданий, контрольных работ и типовых расчетов, зачеты и экзамены. Опросы студентов по содержанию лекций и проверка выполнения текущих заданий проводится на каждом практическом занятии. Результаты проверки фиксируются и сообщаются студенту.
Учебно-тематический план . Специальность финансы и кредит 080105 (очная форма-5 лет обучения)
| № | Тема | Всего часов | В том числе | Формы контроля | |||
| Лекции (час) | Практические занятия (час) | Самостоятельная работа (час) | |||||
| 4 семестр | |||||||
| 1 | Объект, предмет, сущность и основные категории эконометрики. | 3 | 1 | 2 | Текущий контроль | ||
| 2 | Модели парной и множественной регрессии | 9 | 2 | 3 | 4 | Текущий контроль | |
| 3 | Линейные регрессионные модели с переменной структурой | 6 | 1 | 2 | 3 | Текущий контроль | |
| 4 | Мультиколлинеарность | 6 | 1 | 2 | 3 | Текущий контроль | |
| 5 | Гомоскедастичность и гетероскедастичность | 8 | 2 | 2 | 4 | Текущий контроль | |
| 6 | Нелинейные модели регрессии и линеаризация | 6 | 1 | 5 | Текущий контроль | ||
| 7 | Временные ряды | 8 | 2 | 2 | 4 | Текущий контроль | |
| 8 | Модели нестационарных временных рядов | 8 | 2 | 2 | 4 | Текущий контроль | |
| 9 | Системы линейных одновременных уравнений | 6 | 2 | 2 | 2 | Текущий контроль | |
| 10 | Статистические уравнения зависимостей | 8 | 3 | 2 | 3 | Текущий контроль | |
Рубежный контроль
Итоговый контроль
Экзамен
Всего в учебном году
34
Учебно-тематический план . Специальность финансы и кредит 080105 (очная форма-3.5 года обучения)
| № | Тема | Всего часов | В том числе | Формы контроля | |||
| Лекции (час) | Практические занятия (час) | Самостоятельная работа (час) | |||||
| 4 семестр | |||||||
| 1 | Объект, предмет, сущность и основные категории эконометрики. | 3 | 0.5 | 2.5 | |||
| 2 | Модели парной и множественной регрессии | 9 | 0.5 | 1 | 7.5 | ||
| 3 | Линейные регрессионные модели с переменной структурой | 6 | 0.5 | 5.5 | |||
| 4 | Мультиколлинеарность | 6 | 0.5 | 5.5 | |||
| 5 | Гомоскедастичность и гетероскедастичность | 8 | 8 | ||||
| 6 | Нелинейные модели регрессии и линеаризация | 6 | 6 | ||||
| 7 | Временные ряды | 8 | 1 | 1 | 6 | ||
| 8 | Модели нестационарных временных рядов | 8 | 0.5 | 1 | 6.5 | ||
| 9 | Системы линейных одновременных уравнений | 6 | 0.5 | 1 | 4.5 | ||
| 10 | Статистические уравнения зависимостей | 8 | 8 | ||||
|
Рубежный контроль |
| ||||||
| Всего в 4-м семестре | 68 | 4 | 4 | 60 | |||
|
Итоговый контроль |
Экзамен | ||||||
|
Всего в учебном году | 68 | 4 | 4 | 60 | экзамен | ||
Учебно-тематический план . Специальность финансы и кредит 080105 (очная форма-6 лет обучения)
| № | Тема | Всего часов | В том числе | Формы контроля | |||
| Лекции (час) | Практические занятия (час) | Самостоятельная работа (час) | |||||
| 4 семестр | |||||||
| 1 | Объект, предмет, сущность и основные категории эконометрики. | 3 | 0.5 | 2.5 | |||
| 2 | Модели парной и множественной регрессии | 9 | 0.5 | 1 | 7.5 | ||
| 3 | Линейные регрессионные модели с переменной структурой | 6 | 0.5 | 1 | 4.5 | ||
| 4 | Мультиколлинеарность | 6 | 0.5 | 5.5 | |||
| 5 | Гомоскедастичность и гетероскедастичность | 8 | 0.5 | 7.5 | |||
| 6 | Нелинейные модели регрессии и линеаризация | 6 | 0.5 | 1 | 4.5 | ||
| 7 | Временные ряды | 8 | 1 | 1 | 6 | ||
| 8 | Модели нестационарных временных рядов | 8 | 1 | 1 | 6 | ||
| 9 | Системы линейных одновременных уравнений | 6 | 1 | 1 | 4 | ||
| 10 | Статистические уравнения зависимостей | 8 | 8 | ||||
|
Рубежный контроль |
| ||||||
| Всего в 4-м семестре | 68 | 6 | 6 | 56 | |||
|
Итоговый контроль |
Экзамен | ||||||
|
Всего в учебном году | 68 | 6 | 6 | 56 | экзамен | ||
Образовательная программа
Список тем
Тема 1. Объект, предмет, сущность и основные категории эконометрики.
Тема 2. Модели парной и множественной регрессии.
Тема 3. Линейные регрессионные модели с переменной структурой.
Тема 4. Мультиколлинеарность.
Тема 5. Гомоскедастичность и Гетероскедастичность.
Тема 6. Нелинейные модели регрессии и линеаризация.
Тема 7. Временные ряды.
Тема 8 Модели нестационарных временных рядов.
Тема 9. Системы линейных одновременных уравнений.
Тема 10. Статистические уравнения зависимостей.
Реферативное описание тем
Тема 7. Временные ряды.
Понятие временного ряда. Допустимость использования классической модели линейной регрессии для анализа временных рядов. Факторы, влияющие на формирование временных рядов. Стационарные и нестационарные временные ряды.
Автокорреляционная функция. Аналитическое выравнивание временного ряда. Автокорреляция остатков временного ряда. Тесты на наличие автокорреляции. Тест Дарбина-Уотсона. Устранение автокорреляции.
Список основной литературы
1. Эконометрика.: Учебник/ И. И. Елисеева, С. В. Курышева, Т. В. Костеева и др.: Под. ред. И. И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2006. -576 с.: ил.
2. Практикум по эконометрике: Учеб. пособие/ Под ред. И.И. Елисеевой 2-е изд. перераб. и доп. - М., "Финансы и статистика", 2007.
3. Кремер Н. Ш., Путко Б. А. Эконометрика: Учебник для вузов/ Под ред. Кремера Н. Ш. – М.: ЮНИТИ-ДАНА. 2007. – 311 с.
Планы практических занятий
| № | Тема | Содержание | Часы | Лит. источник |
| 1 | 2 | 3 | 4 | 5 |
| 1 | Тема 2.Построение моделей парной регрессии методом наименьших квадратов. | Нахождение уравнений парной регрессии. Вычисление коэффициента корреляции между переменными Х и У. Оценка параметров парной регрессионной модели. Построение доверительных интервалов для функции регрессии и ее параметров. Оценка значимости коэффициентов регрессии. Вычисление коэффициента детерминации. Проверка значимости полученного уравнения регрессии. Построение моделей множественной регрессии . | 3 | [1], [2] |
| 2 | Тема 3.Фиктивные переменные. Критерий Чоу. | Построение линейной регрессионной модели с учетом фиктивных переменных и без учета их. Проверка значимости построенных моделей и сравнение их. | 2 | [1], [2] |
| 3 | Тема 4. Мультиколлинеарность. Тесты на наличие и устранения мультиколлинеарности для оценок параметров регрессионной модели. | Построение матрицы парной корреляции между факторами (х i, х j) и (y, x i) . Анализ полученной матрицы и в случае обнаружения мультиколлинеарности использование процедуры пошагового отбора наиболее информативных переменных. | 2 | [1], [2] |
| 4 | Тема 5. Гомоскедастичность и гетероскедастичность. Тесты на наличие и устранения гетероскедастичности. | Применение теста Голдфелда - Квандта с целью обнаружения гетероскедастичности и в случае наличия ее использование метода взвешенного метода наименьших квадратов. | 2 | [1], [2] |
| 1 | 2 | 3 | 4 | 5 |
| 5 | Тема 7. Временные ряды. Стационарные и нестационарные временные ряды. Автокорреляционная функция. Аналитическое выравнивание временного ряда. | Нахождение среднего значения, среднего квадратического отклонения для временного ряда, коэффициентов автокорреляции для различных лагов и частного коэффициента автокорреляции 1-го порядка. Нахождение уравнения неслучайной составляющей тренда для временного ряда. Проведения сглаживания временного ряда методом скользящих средних. Построение точечной интервальной оценки прогноза средней и индивидуального значений временного ряда. | 2 | [1], [2] |
| 6 | Тема 7. Тесты на наличие автокорреляции и ее устранение. | Использование теста Дарбина-Уотсона для обнаружения автокорреляции и ее устранения. | 2 | [1], [2] |
| 7 | Тема 10. Статистические уравнения зависимостей (однофакторные и многофакторные). | Расчет параметров однофакторных и многофакторных уравнений зависимости. Вычисление коэффициента и индекса корреляции. Вычисление коэффициента устойчивости связи для оценки достоверности эконометрических расчетов. Нормативные расчеты микроэкономических показателей хозяйственной деятельности. Моделирование динамики и прогнозирование экономических процессов. | 2 | [1], [2] |
| 8 | Контрольная. работа | 2 | ||
| Итого | 17 | |||
Глоссарий
1. Уравнение Y t = b 0 + b 1 X t + e t , t = 1,….,n,
где
X t -неслучайная (детерминированная) величина, Y t , b 0 и b 1 – неизвестные параметры, e t -случайные величины, называется линейным регрессионным уравнением.
Y t называется объясняемой ( зависимой) переменной, а X t -объясняющей (независимой) переменной или регрессором
2. Основные гипотезы:
1. Y t = b 0 + b 1 X t + e t , t = 1,….,n, - спецификация модели.
2. X t - детерминированная величина;
3. e i - случайная величина, удовлетворяющая следующим предпосылкам
3а). Ee t = 0, ( ЕY t =b 0 + b 1 X t ), E (e t2) = V(e t) = s 2 , (V(Y t ) = s 2) - не зависит от t.
3б). E(e t e s) = 0 (Cov (Y t , Y s)=0), t ¹ s - некоррелированность ошибок для разных наблюдений.
Часто добавляется условие:
3в). e t ~ N( 0, s 2), т.е. e t - нормально распределенная случайная величина со средним 0 и дисперсией s 2 .
Условие независимости дисперсии ошибки от номера наблюдений E (e t2) = s 2, t = 1,….,n , называется гомоскедастичностью ( а); случай, когда условие гомоскедастичности не выполняется , называется гетероскедастичностью (б).
Теорема Гаусса - Маркова.
Для модели 1 -3ab:
оценки b 0, b 1 параметров регрессии, полученные по методу наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещенных оценок s 2 .
3. Коэффициентом детерминации R 2 или долей объясненной дисперсии называется
R 2 = 1 -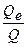 
= 
.
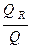Q - вся дисперсия , Q e - остаточная дисперсия, Q R - объясненная часть всей дисперсии.
4.Классическая нормальная линейная модель множественной регрессии.
Модель множественной регрессии:
y i = b 0 + b 1 x i1 + b 2 x i3 + b p x i p + e i i = 1,2, … n;
где х tp - значения регрессора х p в наблюдении t.
Основные гипотезы, лежащие в основе модели множественной регрессии, являются естественным обобщением модели парной регрессии:
1. y i = b 0 + b 1 x i1 + b 2 x i3 + b p x i p + e i i = 1,2, … n;
- спецификация модели.
2. x i 1, x i 2,…. x i p -детерминированные величины. Векторы х s = (x 1s, …. x n s)', s = 1,….p линейно независимы в R n.
3. e i - случайная величина, удовлетворяющая следующим предпосылкам:
3a) Е(e i ) = 0; D (e i ) = s 2 для любого i ;
3б) e i и e j не коррелированы: Е(e i, e j) = 0 при i ¹ j ; выводится из условия некоррелированности Cov (e i , e j) = 0; (Cov (e i , e j) = Е[(e i - 0) ((e j - 0)]) = Е(e i, e j) = 0).
Часто добавляется условие:
3в). e t ~ N(0, s 2), т.е. e t - нормально распределенная случайная величина со средним 0 и дисперсией s 2.
В этом случае модель называется нормальной линейной регрессионной.
Все эти условия удобно записать в матричной форме:
У = Х × b + e или
у i = b 0 +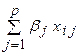 
+ e i , i = 1,2,….n.
где У = (у 1,…у n) ' - вектор значений зависимой переменной ;
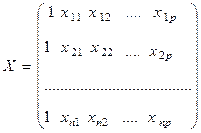- матрица значений объясняющих переменных, в которую дополнительно введен столбец, все элементы которого равны 1, т.е. условно полагается, что модели (МР1) свободный член b 0 умножается на фиктивную переменную х i 0, принимающую значение 1 для всех i :
х i 0 =1 (i = 1,2,….n);
b = (b 0 , b 1 , …… b p)' - вектор параметров размера (р + 1); e = (e 1,e 2,…. e n) - вектор возмущений (случайных ошибок) размера n.
Теорема Гаусса - Маркова.
Предположим, что:
1. у = Х b + e ;
2. Х - детерминированная n ´ (p+1) матрица, имеет максимальный ранг (p+1) ;
3. Е(e ) = 0; Е(e e ') = s 2 1 n.
4. e - нормально распределенный случайный вектор e ~ N(0, s 21 n);
5. r (X) = p + 1 < n
Тогда при выполнении предпосылок (1-3, 5) оценка МНК b = (X ' X) - 1 X ' y является наиболее эффективной ( в смысле наименьшей дисперсии) оценкой в классе линейных (по у ) несмещенных оценок.
5. Ковариационная матрица и ее выборочная оценка.
Вариации оценок параметров будут определять точность уравнения множественной регрессии. Для их вычисления используют ковариационную матрицу вектора оценок параметров å b .
å b =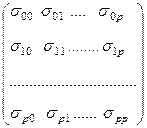 
,
где s ij 2 - ковариации (корреляционные моменты) оценок параметров b i и b j .
s ij 2 = Е[ (b i - Е(b i))(b j - Е(b j))]. (МР7)
Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных.
Оценка дисперсии ошибок s 2. Распределение s 2.
S 2 =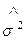 
= 
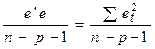
является несмещенной оценкой дисперсии ошибок (возмущений) s 2, т.е. Еs 2 = s 2.
6. Оценка значимости коэффициентов регрессии b j .
Значимость коэффициентов регрессии b j можно проверить, если учесть, что статистика (b j - b j0 )/ s b j имеет t - распределение Стьюдента с к = n - p - 1 степенями свободы. Поэтому b j значимо отличается от нуля ( т.е. гипотеза Н 0 о равенстве параметра b j нулю Н 0 : b j0 = 0, отвергается) на уровне значимости a , если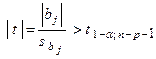 
, где t 1 - a; n - p -1 - табличное значение t - критерия Стьюдента, определенное на уровне значимости a при числе степеней свободы к = n - p - 1.
7. Доверительный интервал для параметра b j есть
b j - t 1 - a; n - p -1 s b j £ b j £ b j + t 1 - a; n - p -1 s b
8. Доверительный интервал для функции регрессии или для условного математического ожидания зависимой переменной Е х(У):
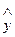- t 1 - a; k 
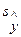< Е(Y) < 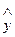+ t 1 - a; k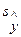
где 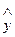- групповая средняя, определяемая по уравнению регрессии,
= 
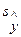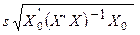- ее стандартная ошибка.
9. Доверительный интервал для индивидуальных значений зависимой переменной у *0 примет вид:
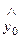- t 1 - a; n - p -1 
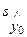< у *0 < 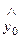+ t 1 - a; n - p - 1 ,
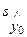где =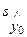 
.
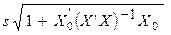10. Доверительный интервал для параметра s 2 в множественной регрессии:
.
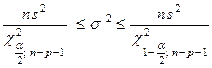11.Оценка значимости уравнения регрессии.
Проверить значимость уравнения регрессии - значит установить, соответствует ли математическая модель, выражающая зависимость между переменными и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной.
При отсутствии линейной зависимости между зависимой переменной и объясняющей переменными несмещенные оценки дисперсий s2R = QR/(m - 1) и s2e = Qe/(n - m) имеют c 2 -распределение с соответственно к = m - 1 и к = n - m степенями свободы, а их отношение - F -распределение с теми же степенями свободы. Поэтому уравнение регрессии значимо на уровне a , если фактически наблюдаемое значение статистики
F =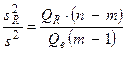 
> Fa; k1;k2 ,
где Fa; k1;k2 - табличное значение F - критерия Фишера - Снедекера, определенное на уровне значимости a при к 1 = m - 1 и к 2 = n - m степенях свободы.
Значение F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.
12.Оценка значимости коэффициента корреляции при отсутствии корреляционной связи статистика t =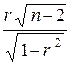 
имеет распределение Стьюдента с (n - 2) степенями свободы. Коэффициент корреляции r значим на уровне a (т.е. гипотеза Н 0 о равенстве генерального коэффициента корреляции r = 0 отвергается ), если
½ t½ =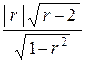 
> t 1 - a; n - 2 .
13. Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных.
14. Автокорреляции ошибок, если E(e t e s) = r ¹ 0,
15.Стандартизированные коэффициенты регрессии b'j и коэффициенты эластичности Е j (j = 1,….p):
b'j =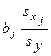 
;
E j =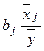 
.
Стандартизированный коэффициент регрессии b'j показывает, на сколько величин s y изменится в среднем зависимая переменная У при увеличении только j -ой объясняющей переменной на s x j , а коэффициент эластичности Е j - на сколько процентов (от средней) изменится в среднем У при увеличении только Х j на 1 %.
16. Временным рядом (динамическим рядом или рядом динамики) в экономике называется последовательность наблюдений некоторого признака (случайной величины) У в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда, которые обозначаются у t (t = 1,2,….n), где n - число уровней.
В общем виде при исследовании экономического временного ряда у t выделяются несколько составляющих:
у t = u t + n t + c t + e t t = 1,2,….n,
где u t - тренд,
n t - сезонная компонента,
c t - циклическая компонента,
e t - случайная компонента,
u t, n t , c t - закономерные, неслучайные составляющие.
17. Стационарные временные ряды.
Временной ряд у t (t=1,2,…,n) называется строго стационарным, если совместное распределение вероятностей n наблюдений у 1, у 2,…..уn такое же, как и n наблюдений у 1 + t , у 2 + t ,…у n + t при любых n, t и t , т.е. свойства строго стационарных рядов у t (закон распределения и его числовые характеристики) не зависят от момента t .
18. Степень тесноты связи между последовательностями наблюдений временного ряда у 1, у 2,…у n и у 1 + t , у 2 + t ,….у n + t (сдвинутых относительно друг друга на t единиц, т.е. с лагом t ) может быть определена с помощью коэффициента корреляции
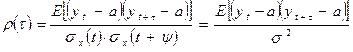
так как Е(у t) = Е(у t + t) = a, s y(t) = s y(t + t) = s.
Так как коэффициент r(t) измеряет корреляцию между членами одного и того же ряда, его называют коэффициентом автокорреляции, а зависимость r(t) - автокорреляционной функцией. В силу стационарности временного ряда у t автокорреляционная функция r(t) зависит от лага t , причем r( - t) = r(t), т.е. при r(t) можно ограничиться рассмотрением только положительных значений t.
19. Статистической оценкой r ( t ) является выборочный коэффициент автокорреляции r(t) , определяемый по формуле
r(t) =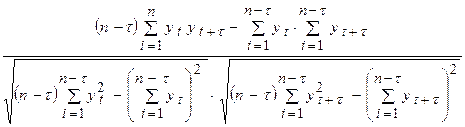 
.
Функцию r(t) называют выборочной автокорреляционной функцией, а ее график - коррелограммой.
Контрольные вопросы к итоговой аттестации
1. Предмет, задачи, критерии и принципы эконометрики.
2.Типы моделей, используемые для анализа и прогноза экономических процессов.
3.Метод наименьших квадратов.
4.Основные эконометрические методы.
5. Построение модели парной регрессии.
6. Теорема Гаусса - Маркова.
7.Построение модели множественной регрессии.
8.Оценка коэффициентов линейной регрессии.
9.Коэффициент корреляции.
10. Коэффициент детерминации.
11.Мультиколлинеарность. Тесты на наличие мультиколлинеарности.
12.Тесты на устранение мультиколлинеарности.
13. Гомогедастичность и гетероскедастичность. Тесты на наличие гетероскедастичности
13. Тесты на устранение гетероскедастичности.
14.Фиктивные переменные. Критерий Чоу.
15.Временные ряды. Стационарные и нестационарные временные ряды.
16.Автокорреляция остатков временного ряда. Тесты на наличие автокорреляции.
17. Устранение автокорреляции.
18. Понятие об авторегрессионных моделях.
19. Модели скользящей средней.
20.Метод инструментальных переменных.
21.Оценивание моделей с распределенными лагами.
22. Системы одновременных уравнений.
23. Двухшаговый метод наименьших квадратов.
24. Трехшаговый метод наименьших квадратов.
Цели и задачи курса
Целью изучения дисциплины «Эконометрика» является развитие математического мышления и навыков использования математических методов и основ математического моделирования в макроэкономике
Дисциплина «Эконометрика» предназначена для выработки у студентов умения проводить строгий логический и количественный анализ процессов в области макроэкономики с построением моделей их описания для прогнозирования явлений;
В результате изучения дисциплины студент должен знать и уметь использовать:
§ основы теории вероятностей и математической статистики;
§ математические методы при изучении социально-экономических процессов в различных областях экономики;
§ математические методы и модели при исследовании и решении задач управления экономическими системами с использованием различных средств информационного обеспечения.
Для выработки у современных специалистов по финансам и кредиту необходимой научной культуры программа по «Эконометрике» предусматривает реализацию следующей основной задачи: ориентация на обучение и выработку у студентов навыков и умения строить и использовать эконометрические модели для описания и прогнозирования различных процессов в области экономики.
Связь с другими дисциплинами.
Курс базируется на дисциплинах "Теория вероятностей" и "Математическая статистика", "Многомерные статистические методы", "Статистический анализ нечисловой информации". С другой стороны он является основой для дисциплины "Эконометрическое моделирование".
Виды занятий и методика обучения
Курс эконометрики изучается в одном семестре в форме лекций и практических занятий. Предусмотрена самостоятельная подготовка студентов.
На лекциях излагается содержание дисциплины, проводится анализ основных понятий и методов. Чтение лекций сопровождается рассмотрением примеров, соответствующих основным положениям лекций и должно быть логичным, наглядным, ориентированным на последующие приложения излагаемого материала в других дисциплинах.
На практических занятиях студент овладевает основными методами и приемами решения задач, а также получает разъяснение теоретических положений курса. При подборе задач следует стремится выбрать те из них, которые возникают в соответствующих приложениях и в процессе решения задач давать интерпретацию и трактовку.
При проведении практических занятий со студентами рекомендуется обращать особое внимание:
§ на развитие аналитических и вычислительных способностей и формирование соответствующих навыков;
§ на привитие навыков составления и анализа математических моделей простых реальных задач;
§ на выработку умения решать прикладные задачи, связанные с будущей специальностью студента, требующие отбора данных и предварительного вывода аналитических зависимостей;
§ методам контроля правильности решения задач.
Самостоятельная работа студентов является важной формой усвоения курса математики. Она должна состоять из непрерывной работы студента по выполнению текущих заданий и типовых расчетов. Типовой расчет является индивидуальным заданием по разделам (темам), изучаемым в семестре. Он состоит из теоретических вопросов (8 - 10), задач и примеров (8 - 10). Теоретические вопросы и упражнения являются общими для всех студентов, задачи и примеры индивидуальны.
Формы контроля
Результативность самостоятельной работы студентов обеспечивается эффективной системой контроля, включающей в себя вопросы по содержанию лекций и проверку выполнения текущих заданий, контрольных работ и типовых расчетов, зачеты и экзамены. Опросы студентов по содержанию лекций и проверка выполнения текущих заданий проводится на каждом практическом занятии. Результаты проверки фиксируются и сообщаются студенту.
Учебно-тематический план . Специальность финансы и кредит 080105 (очная форма-5 лет обучения)
| № | Тема | Всего часов | В том числе | Формы контроля | |||
| Лекции (час) | Практические занятия (час) | Самостоятельная работа (час) | |||||
| 4 семестр | |||||||
| 1 | Объект, предмет, сущность и основные категории эконометрики. | 3 | 1 | 2 | Текущий контроль | ||
| 2 | Модели парной и множественной регрессии | 9 | 2 | 3 | 4 | Текущий контроль | |
| 3 | Линейные регрессионные модели с переменной структурой | 6 | 1 | 2 | 3 | Текущий контроль | |
| 4 | Мультиколлинеарность | 6 | 1 | 2 | 3 | Текущий контроль | |
| 5 | Гомоскедастичность и гетероскедастичность | 8 | 2 | 2 | 4 | Текущий контроль | |
| 6 | Нелинейные модели регрессии и линеаризация | 6 | 1 | 5 | Текущий контроль | ||
| 7 | Временные ряды | 8 | 2 | 2 | 4 | Текущий контроль | |
| 8 | Модели нестационарных временных рядов | 8 | 2 | 2 | 4 | Текущий контроль | |
| 9 | Системы линейных одновременных уравнений | 6 | 2 | 2 | 2 | Текущий контроль | |
| 10 | Статистические уравнения зависимостей | 8 | 3 | 2 | 3 | Текущий контроль | |
Рубежный контроль
Итоговый контроль
Экзамен
Всего в учебном году
34
Учебно-тематический план . Специальность финансы и кредит 080105 (очная форма-3.5 года обучения)
| № | Тема | Всего часов | В том числе | Формы контроля | |||
| Лекции (час) | Практические занятия (час) | Самостоятельная работа (час) | |||||
| 4 семестр | |||||||
| 1 | Объект, предмет, сущность и основные категории эконометрики. | 3 | 0.5 | 2.5 | |||
| 2 | Модели парной и множественной регрессии | 9 | 0.5 | 1 | 7.5 | ||
| 3 | Линейные регрессионные модели с переменной структурой | 6 | 0.5 | 5.5 | |||
| 4 | Мультиколлинеарность | 6 | 0.5 | 5.5 | |||
| 5 | Гомоскедастичность и гетероскедастичность | 8 | 8 | ||||
| 6 | Нелинейные модели регрессии и линеаризация | 6 | 6 | ||||
| 7 | Временные ряды | 8 | 1 | 1 | 6 | ||
| 8 | Модели нестационарных временных рядов | 8 | 0.5 | 1 | 6.5 | ||
| 9 | Системы линейных одновременных уравнений | 6 | 0.5 | 1 | 4.5 | ||
| 10 | Статистические уравнения зависимостей | 8 | 8 | ||||
|
Рубежный контроль |
| ||||||
| Всего в 4-м семестре | 68 | 4 | 4 | 60 | |||
|
Итоговый контроль |
Экзамен | ||||||
|
Всего в учебном году | 68 | 4 | 4 | 60 | экзамен | ||
Учебно-тематический план . Специальность финансы и кредит 080105 (очная форма-6 лет обучения)
| № | Тема | Всего часов | В том числе | Формы контроля | |||
| Лекции (час) | Практические занятия (час) | Самостоятельная работа (час) | |||||
| 4 семестр | |||||||
| 1 | Объект, предмет, сущность и основные категории эконометрики. | 3 | 0.5 | 2.5 | |||
| 2 | Модели парной и множественной регрессии | 9 | 0.5 | 1 | 7.5 | ||
| 3 | Линейные регрессионные модели с переменной структурой | 6 | 0.5 | 1 | 4.5 | ||
| 4 | Мультиколлинеарность | 6 | 0.5 | 5.5 | |||
| 5 | Гомоскедастичность и гетероскедастичность | 8 | 0.5 | 7.5 | |||
| 6 | Нелинейные модели регрессии и линеаризация | 6 | 0.5 | 1 | 4.5 | ||
| 7 | Временные ряды | 8 | 1 | 1 | 6 | ||
| 8 | Модели нестационарных временных рядов | 8 | 1 | 1 | 6 | ||
| 9 | Системы линейных одновременных уравнений | 6 | 1 | 1 | 4 | ||
| 10 | Статистические уравнения зависимостей | 8 | 8 | ||||
|
Рубежный контроль |
| ||||||
| Всего в 4-м семестре | 68 | 6 | 6 | 56 | |||
|
Итоговый контроль |
Экзамен | ||||||
|
Всего в учебном году | 68 | 6 | 6 | 56 | экзамен | ||
Образовательная программа
Список тем
Тема 1. Объект, предмет, сущность и основные категории эконометрики.
Тема 2. Модели парной и множественной регрессии.
Тема 3. Линейные регрессионные модели с переменной структурой.
Тема 4. Мультиколлинеарность.
Тема 5. Гомоскедастичность и Гетероскедастичность.
Тема 6. Нелинейные модели регрессии и линеаризация.
Тема 7. Временные ряды.
Тема 8 Модели нестационарных временных рядов.
Тема 9. Системы линейных одновременных уравнений.
Тема 10. Статистические уравнения зависимостей.
Реферативное описание тем
Дата: 2018-12-21, просмотров: 397.
