Cловесно-логическое мышление представляет собой совершении любых логических действий (анализа, обобщения, выделения главного при построении выводов) и операций со словами.
Упражнение №15. "Систематизация".
Упражнение направлено на развитие умения систематизировать слова по определенному признаку.
"Скажите, какие ягоды вы знаете?
Сейчас я буду называть слова, если среди них вы услышите слово, обозначающее ягоду, то хлопните в ладоши".
Слова для предъявления - капуста, земляника, яблоко, груша, смородина, малина, морковь, клубника, картофель, укроп, черника, брусника, слива, клюква, абрикос, кабачок, апельсин.
"Сейчас я буду называть слова, если услышите слово, относящееся к ягодам, хлопните один раз, если к фруктам - два раза".
(Слова можно использовать те же самые, можно придумать другие.)
В качестве основания для систематизации может быть тема - инструменты, мебель, одежда, цветы и т.д.
"Скажи, чем похожи по вкусу? цвету? величине?
лимон и груша
малина и земляника
яблоко и слива
смородина и крыжовник
Чем отличаются по вкусу? цвету? величине?"
Упражнение №16. "Раздели на группы".
"Как ты думаешь, на какие группы можно разделить эти слова? Саша, Коля, Лена, Оля, Игорь, Наташа.
Какие группы можно составить из этих слов: голубь, воробей, карп, синица, щука, снегирь, судак".
Упражнение №17. "Подбери слова".
1) "Подбери как можно больше слов, которые можно отнести к группе дикие животные (домашние животные, рыбы, цветы, погодные явления, времена года, инструменты и т.д.)".
2) Другой вариант этого же задания.
"Соедини стрелочками слова, подходящие по смыслу:
мяч мебель
тополь цветок
шкаф насекомые
тарелка дерево
пальто одежда
муравей посуда
щука игрушка
роза рыба"
Подобные задания развивают у ребенка способность выделять родовые и видовые понятия, формируют индуктивное речевое мышление.
Упражнение №18. "Найди общее слово".
В этом задании содержатся слова, которые объединены общим смыслом. Этот их общий смысл нужно постараться передать одним словом. Упражнение направлено на развитие такой функции, как обобщение, а также способность к абстракции.
"Каким общим словом можно назвать следующие слова:
1. Вера, Надежда, Любовь, Елена
2. а, б, с, в, н
3. стол, диван, кресло, стул
4. понедельник, воскресенье, среда, четверг
5. январь, март, июль, сентябрь".
Слова для нахождения обобщающего понятия можно подобрать из любых групп, более или менее конкретных. Например, обобщающим может быть слово "весенние месяцы", а может быть "месяцы года" и т.д.
Более сложный вариант упражнения содержит только два слова, для которых необходимо найти общее понятие.
"Найди, что общего у следующих слов:
а) хлеб и масло (еда)
б) нос и глаза (части лица, органы чувств)
в) яблоко и земляника (плоды)
г) часы и градусник (измерительные приборы)
д) кит и лев (животные)
е) эхо и зеркало (отражение)"
Подобные упражнения стимулируют мышление ребенка к поиску обобщающего основания. Чем выше уровень обобщения, тем лучше развита у ребенка способность к абстрагированию.
Очень эффективным с точки зрения развития обобщающей функции является следующее упражнение.
Упражнение №19. "Необычное домино".
Это упражнение направлено на постепенное (поуровневое) обучение ребенка поиску признаков, по которым может происходить обобщение.
Эмпирически выделяются три сферы таких признаков.
Первая сфера - обобщение по атрибутивному свойству (самый низкий уровень). Сюда входят: форма предмета, его величина, части, из которых он сделан, или материал, цвет, т.е. все то, что является некими внешними качествами, или атрибутами предмета. Например, "кошка и мышка подходят друг к другу, т.к. у них по четыре лапы" или "яблоко и земляника, у них общее то, что они красные...". Кроме того, это может быть использование имени предмета, например, "... тарелка и таз, общее то, что оба предмета начинаются на букву "т".
Вторая сфера - обобщение по ситуативному основанию (более высокий уровень). Переходным к этой сфере является обобщение предметов по признаку "свойство - действие", т.е. ребенок выделяет в качестве общего свойства действие, производимое предметами.
Например, "лягушка подходит к белке, т.к. они умеют прыгать". Кроме того, к этой сфере относятся обобщения по ситуации употребления "груша и морковь, потому что и то и другое едят..."; ситуации места и время нахождения - "кошка и мышка, потому что живут в одном доме"; ситуации общения, игры - "щенок и ежик, потому что вместе играют...".
Третья сфера - обобщение по категориальному признаку (наиболее высокий). Это обобщение по признаку того класса, к которому относятся предметы. Например, мяч и мишка - это игрушки; паук и бабочка, общее то, что это насекомые.
Упражнение "домино" позволяет ребенку самому выбирать основание для обобщения (тем самым взрослый может составить представление об уровне развития данной функции у ребенка), а также направлять и помогать ребенку искать более значимые, высокие по степени признаки для обобщения.
В игре могут принимать участие двое или несколько детей. Кроме того, взрослый сам может быть участником игры.
Игра состоит из 32 карточек, на каждой из которых изображены две картинки.

1. трактор - олень 11. обезьяна - цветок
2. ведро - зебра 12. бабочка - свинья
3. щенок - мышь 13. белка - пирамидка
4. кошка - кукла 14. мяч - мак
5. девочка - мишка 15. птица - ваза
6. слон - елка 16. теленок - самолет
7. грибок - морковь 17. вертолет - цыпленок
8. груша - улитка 18. ежик - мельница
9. паук - утенок 19. домик - яблоко
10. рыба - месяц 20. петух - клубника
21. заяц - вишня 27. львенок - кораблик
22. земляника - аист 28. тележка - чашка
23. пингвин - лягушка 29. чайник - карандаш:
24. солнце - гусеница 30. собака - береза
25. лист - мухомор 31. котенок - апельсин
26. сливы - лев 32. конура - жук
Каждому из участников игры раздается одинаковое количество карточек. После этого разыгрывается право первого хода.
Тот, кто ходит, выкладывает любую карточку. Затем организующий игру говорит: "Перед вами лежит карточка с изображением... . Необходимо, для того чтобы осуществить ход, подобрать какую-нибудь из своих карточек, но с условием, чтобы выбранная вами картинка имела что-то общее с той, к которой вы ее подобрали".
(Во избежание выполнения ребенком задания только одним способом необходимо объяснить, каким образом можно осуществлять подбор. Кроме того, во время игры необходимо постоянно стимулировать ребенка вопросами типа "А что еще общего может быть между подобранными картинками?", на выбор разных оснований для обобщения).
"Одновременно вы должны объяснить, почему был сделан такой выбор, сказать, что же общего между подобранными картинками. Следующий из вас будет опять подбирать картинку к одной из двух, лежащих на кону, объясняя свой выбор".
Таким образом, в результате игры выстраивается цепочка картинок, логически связанных между собой. Напоминаем, что, как и в обычном домино, двусторонность картинок обеспечивает возможность хода как в одну, так и в другую сторону.
За каждый ход начисляются очки. Если обобщение произведено по атрибутивному свойству - 0 очков, по ситуативному основанию - 1 очко, по категориальному признаку - 2 очка. Выигрывает тот, кто набрал больше всего очков.
Карточки, которые получают игроки во время раздачи, ребята не показывают друг другу.
Логические задачи.
Логические задачи - особый раздел по развитию словесно-логического мышления, включающий в себя целый ряд разнообразных упражнений.
Логические задачи предполагают осуществление мыслительного процесса, связанного с использованием понятий, логических конструкций, существующих на базе языковых средств.
В ходе такого мышления происходит переход от одного суждения к другому, их соотношение через опосредование содержания одних суждений содержанием других, и как следствие формулируется умозаключение.
Как отмечал С.Л.Рубинштейн, "в умозаключении... знание добывается опосредованно через знание без каких-либо заимствований в каждом отдельном случае из непосредственного опыта".
Развивая словесно-логическое мышление через решение логических задач, необходимо подбирать такие задачи, которые бы требовали индуктивного (от единичного к общему), дедуктивного (от общего к единичному) и традуктивного (от единичного к единичному или от общего к общему, когда посылки и заключение являются суждениями одинаковой общности) умозаключения.
Традуктивное умозаключение можно использовать в качестве первой ступени обучения умению решать логические задачи. Это задачи, в которых по отсутствию или присутствию одного из двух возможных признаков у одного из двух обсуждаемых объектов следует вывод о, соответственно, присутствии или отсутствии этого признака у другого объекта. Например, "у Наташи собачка маленькая и пушистая, у Иры - большая и пушистая. Что в этих собачках одинаковое? разное?"
Задачи для решения.
1. Саша ел яблоко большое и кислое. Коля ел яблоко большое и сладкое. Что в этих яблоках одинаковое? разное?
2. Маша и Нина рассматривали картинки. Одна девочка рассматривала картинки в журнале, а другая девочка - в книжке. Где рассматривала картинки Нина, если Маша не рассматривала картинки в журнале?
3. Толя и Игорь рисовали. Один мальчик рисовал дом, а другой - ветку с листьями. Что рисовал Толя, если Игорь не рисовал дом?
4. Алик, Боря и Вова жили в разных домах. Два дома были в три этажа, один дом был в два этажа. Алик и Боря жили в разных домах, Боря и Вова жили тоже в разных домах. Где жил каждый мальчик?
5. Коля, Ваня и Сережа читали книжки. Один мальчик читал о путешествиях, другой - о войне, третий - о спорте. Кто о чем читал, если Коля не читал о войне и о спорте, а Ваня не читал о спорте?
6. Зина, Лиза и Лариса вышивали. Одна девочка вышивала листочки, другая - птичек, третья - цветочки. Кто что вышивал, если Лиза не вышивала листочки и птичек, а Зина не вышивала листочки?
7. Мальчики Слава, Дима, Петя и Женя сажали плодовые деревья. Кто-то из них сажал яблони, кто-то - груши, кто-то - сливы, кто-то - вишни. Что сажал каждый мальчик, если Дима не сажал сливы, яблони и груши, Петя не сажал груши и яблони, а Слава не сажал яблони?
8. Девочки Ася, Таня, Ира и Лариса занимались спортом. Кто-то из них играл в волейбол, кто-то плавал, кто-то бегал, кто-то играл в шахматы. Каким спортом увлекалась каждая девочка, если Ася не играла в волейбол, в шахматы и не бегала, Ира не бегала и не играла в шахматы, а Таня не бегала?
Эти восемь задач имеют три степени сложности. Задачи 1-3 - самые простые, для их решения достаточно оперировать одним суждением. Задачи 4-6 - второй степени сложности, поскольку при их решении необходимо сопоставить два суждения. Задачи 7 и 8 - самые сложные, т.к. для их решения нужно соотнести три суждения.
Обычно трудности, возникающие при решении задач с 4 по 8, связаны с невозможностью удержать во внутреннем плане, в представлении все обстоятельства, указанные в тексте, и они путаются, поскольку не пытаются рассудить, а стремятся увидеть, представить правильный ответ. Эффективен в этом случае прием, когда ребенок имеет возможность опираться на наглядные представления, помогающие ему удержать все текстовые обстоятельства.
Например, взрослый может сделать картинки домиков (задача № 4). А затем с опорой на них проводить рассуждение такого типа: "Если Алик и Боря жили в разных домах, то в каких из нарисованных они могли бы жить? А почему не в первых двух? и т.д.
К задачам 7 и 8 удобнее сделать таблицу, которая будет заполняться по мере рассуждения. Например, таблица к задаче №7:
|
"Известно, что Дима не сажал сливы, яблони и груши. Следовательно, около этих деревьев рядом с Димой мы можем поставить прочерк. Тогда, что же сажал Дима? Правильно, осталась только одна свободная клеточка, т.е. Дима сажал вишни. Поставим в этой клетке знак "+" и т.д."
Графическое отражение структуры хода рассуждения помогает ребенку уяснить общий принцип построения и решения задач такого типа, что в последующем делает успешной мыслительную деятельность ребенка, позволяя справляться с задачами более сложной структуры.
Следующий вариант задач содержит следующее исходное положение: если даны три объекта и два признака, одним из которых обладают два объекта, а другим один, то, зная, какие два объекта отличаются от третьего по указанным признакам, можно легко определить, каким признаком обладают первые два. При решении задач подобного типа ребенок учится совершать следующие мыслительные операции:
- делать вывод об идентичности двух объектов из трех по указанному признаку. Например, если в условии сказано, что Ира и Наташа и Наташа с Олей вышивали разные картинки, то понятно, что Ира и Оля вышивали одинаковую;
- делать вывод о том, каков тот признак, по которому эти два объекта идентичны. Например, если в задаче сказано, что Оля вышивала цветок, следовательно, Ира тоже вышивала цветок;
- делать окончательный вывод, т.е. исходя из того, что уже известны два объекта из четырех, которые идентичны по одному из двух данных в задаче признаков, ясно, что другие два объекта идентичны по другому из двух известных признаков. Так, если Ира и Оля вышивали цветок, то другие две девочки, Наташа и Оксана, вышивали домик.
Задачи для решения.
1. Две девочки сажали деревья, а одна - цветы. Что сажала Таня, если Света с Ларисой и Лариса с Таней сажали разные растения?
2. Три девочки нарисовали двух кошек и одного зайца, каждая по одному животному. Что нарисовала Ася, если Катя с Асей и Лена с Асей нарисовали разных животных?
3. Два мальчика купили марки, один - значок и один - открытку. Что купил Толя, если Женя с Толей и Толя с Юрой купили разные предметы, а Миша купил значок?
4. Два мальчика жили на одной улице, а два - на другой. Где жили Петя и Коля, если Олег с Петей и Андрей с Петей жили на разных улицах?
5. Две девочки играли в куклы, а две - в мяч. Во что играла Катя, если Алена с Машей и Маша со Светой играли в разные игры, а Маша играла в мяч?
6. Ира, Наташа, Оля и Оксана вышивали разные картинки. Две девочки вышивали цветок, две - домик. Что вышивала Наташа, если Ира с Наташей и Наташа с Олей вышивали разные картинки, а Оксана вышивала домик?
7. Мальчики читали разные книги: один - сказки, другой - стихи, двое других - рассказы. Что читал Витя, если Леша с Витей и Леша с Ваней читали разные книги, Дима читал стихи, а Ваня с Димой тоже читали разные книги?
8. Две девочки играли на пианино, одна на скрипке и одна на гитаре. На чем играла Саша, если Юля играла на гитаре, Саша с Аней и Марина с Сашей играли на разных инструментах, а Аня с Юлей и Марина с Юлей тоже играли на разных инструментах?
9. Две девочки плыли быстро и две медленно. Как плыла Таня, если Ира с Катей и Ира с Таней плыли с разной скоростью, Света плыла медленно, а Катя со Светой тоже плыли с разной скоростью?
10. Два мальчика сажали морковь и два - картошку. Что сажал Сережа, если Володя сажал картофель, Валера с Сашей и Саша с Володей сажали разные овощи, а Валера с Сережей тоже сажали разные овощи?
Задачи на сравнение.
В основе этого типа задач лежит такое свойство отношения величин объектов, как транзитивность, состоящее в том, что если первый член отношения сравним со вторым, а второй с третьим, то первый сравним с третьим.
Начинать обучение решению таких задач можно с самых простых, в которых требуется ответить на один вопрос и которые опираются на наглядные представления.
1. "Галя веселее Оли, а Оля веселее Иры. Нарисуй рот Иры. Раскрась красным карандашом рот самой веселой девочки.
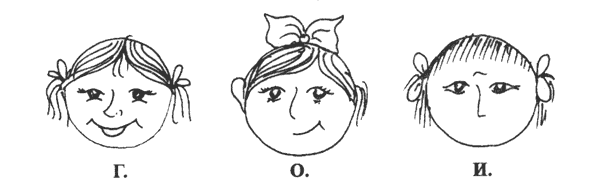
Кто из девочек самый грустный?
2. "Волосы у Инны темнее, чем у Оли. Волосы у Оли темнее, чем у Ани. Раскрась волосы каждой девочки. Подпиши их имена. Ответь на вопрос, кто светлее всех?"

3. "Толя выше Игоря, Игорь выше Коли. Кто выше всех? Покажи рост каждого мальчика".

Графическое изображение транзитивного отношения величин значительно упрощает понимание логической структуры задачи. Поэтому, когда ребенок затрудняется, мы советуем использовать прием изображения отношения величин на линейном отрезке. Например, дана задача: "Катя быстрее Иры, Ира быстрее Лены. Кто быстрее всех?". В этом случае объяснение может строиться следующим образом: "Посмотри внимательно на эту линию.

С одной стороны располагаются дети самые быстрые, с другой - медленные. Если Катя быстрее Иры, то где мы поместим Катю, а где Иру? Правильно, Катя будет справа, где быстрые дети, а Ира слева, т.к. она более медлительна. Теперь сравним Иру и Лену.

Мы знаем, что Ира быстрее Лены. Где мы тогда поместим Лену относительно Иры? Правильно, еще левее, т.к. она медленнее Иры.

Посмотри внимательно на чертеж. Кто же быстрее всех? а медленнее?".
Ниже мы приводим варианты логических задач, которые делятся по степени сложности на три группы:
1) задачи 1-12, в которых требуется ответить на один вопрос;
2) задачи 12-14, в которых нужно ответить на два вопроса;
3) задачи 15 и 16, решение которых предполагает ответ на три вопроса.
Условия задач различаются не только по количеству информации, в которой нужно разобраться, но и по ее наблюдаемым особенностям: виды отношений, разные имена, поставленный по-разному вопрос. Особое значение имеют "сказочные" задачи, в которых отношения между величинами построены таким образом, каких в жизни не бывает. Важно, чтобы ребенок смог отвлечься от жизненного опыта и пользовался теми условиями, какие даются в задаче.
Варианты задач.
1. Саша грустнее, чем Толик. Толик грустнее, чем Алик. Кто веселее всех?
2. Ира аккуратнее, чем Лиза. Лиза аккуратнее, чем Наташа. Кто самый аккуратный?
3. Миша сильнее, чем Олег. Миша слабее, чем Вова. Кто сильнее всех?
4. Катя старше, чем Сережа. Катя младше, чем Таня. Кто младше всех?
5. Лиса медлительнее черепахи. Лиса быстрее, чем олень. Кто самый быстрый?
6. Заяц слабее, чем стрекоза. Заяц сильнее, чем медведь. Кто самый слабый?
7. Саша на 10 лет младше, чем Игорь. Игорь на 2 года старше, чем Леша. Кто младше всех?
8. Ира на 3 см ниже, чем Клава. Клава на 12 см выше, чем Люба. Кто выше всех?
9. Толик намного легче, чем Сережа. Толик немного тяжелее, чем Валера. Кто легче всех?
10. Вера немного темнее, чем Люда. Вера намного светлее, чем Катя. Кто светлее всех?
11. Леша слабее, чем Саша. Андрей сильнее, чем Леша. Кто сильней?
12. Наташа веселее, чем Лариса. Надя грустнее, чем Наташа. Кто самый грустный?
13. Света старше, чем Ира, и ниже, чем Марина. Света младше, чем Марина, и выше, чем Ира. Кто самый младший и кто ниже всех?
14. Костя сильнее, чем Эдик, и медленнее, чем Алик. Костя слабее, чем Алик, и быстрее, чем Эдик. Кто самый сильный и кто самый медлительный?
15. Оля темнее, чем Тоня. Тоня ниже, чем Ася. Ася старше, чем Оля. Оля выше, чем Ася. Ася светлее, чем Тоня. Тоня младше, чем Оля. Кто самый темный, самый низкий и самый старший?
16. Коля тяжелее, чем Петя. Петя грустнее, чем Паша. Паша слабее, чем Коля. Коля веселее, чем Паша. Паша легче, чем Петя. Петя сильнее, чем Коля. Кто самый легкий, кто веселее всех, кто самый сильный?
Все рассмотренные нами варианты логических задач направлены на создание условий, в которых существует или существовала бы возможность формирования способности выделять существенные отношения между объектами и величинами.
Кроме тех задач, которые были указаны выше, целесообразно предлагать ребенку задачи, в которых отсутствует часть необходимых данных или, наоборот, имеются ненужные данные. Можно также использовать прием самостоятельного составления задач по аналогии с данной, но с другими именами и иным признаком (если в задаче имеется признак "возраст", то это может быть задача про "рост" и т.д.), а также задач с недостающими и избыточными данными. Имеет смысл превращение прямых задач в обратные и наоборот. Например, прямая задача: "Ира выше Маши, Маша выше Оли, кто выше всех?"; в обратной задаче вопрос: "Кто ниже всех?".
Если ребенок успешно справляется со всеми видами предложенных ему задач, целесообразно предлагать задания, связанные с творческим подходом:
- придумать задачу, которая как можно более не похожа на задачу-образец, но построена по единому с ней принципу;
- придумать задачу, которая была бы сложнее, например, содержала бы больше данных, чем образец;
- придумать задачу, которая была бы проще, чем задача-образец, и т.д.
Упражнение №20. "Анаграмма".
В основе этого упражнения лежат задачи комбинаторного типа, т.е. такие, в которых решение получается в результате создания неких комбинаций. Примером таких комбинаторных задач являются анаграммы - буквосочетания, из которых необходимо составлять осмысленные слова.
Предложите ребенку составить слово из определенного набора букв. Начните с 3 букв, постепенно доведя количество до 6-7, а может быть, и 8 и даже 9 букв.
"Составь слова из следующих букв:
а) к, о, с а) е, р, о, м а) л, а, н, е, п
б) у, д, б б) ш, а, к, а б) к, ч, а, р, у
в) м, р, и в) а, к, у, р в) ч, а, к, о, с
г) т, о, р г) б, о, н, е г) п, о, г, и, р
д) ы, с, р д) а, с, о, к д) р, о, д, о, г
е) д, м, ы е) д, а, в, о е) к, к, о, а, ш"
После того, как ребенок усвоит принцип составления слов из буквосочетаний, усложните задание. С этой целью введите новое условие: "Расшифруй, какие тут спрятаны слова, и скажи, какое слово из данных лишнее".
1) с, л, у, т 2) ш, у, г, а, р 3) с, б, а, а, к, о
ш, а, ф, к е, р, а, з, б, е о, о, р, к, а, в
ж, о, а, к, л б, я, я, о, л, н ш, к, к, о, а
к, ь, в, а, р, т, о н, о, и, л, м в, ь, я, и, с, н
с, л, т, о а, с, в, и, л я, а, ц, з
Задание может быть и другого типа: "Расшифруй слова и скажи, каким общим словом их можно объединить".
1) п, и, к, а, т 2) ь, о, ч, н 3) й, е, н, и
т, ф, и, у, л ч, е, е, р, в д, а, р, г
б, и, и, т, н, о, к у, о, р, т с, г, е, н
г, а, о, п, и, с н, е, д, ь ь, д, д, о, ж
Еще вариант задания с анаграммами: "Расшифруй слова и скажи, на какие группы их можно разделить".
1) е, м, р, о 2) к, у, а, п 3) а, к, о, р, о, с
р, а, е, к з, я, а, ц в, л, е
ш, а, а, м, р, о, к а, и, с, л щ, а, у, к
о, о, е, з, р х, м, а, у а, а, ь, с, р, к
ь, ю, т, л, н, а, п м, й, е, в, а, у, р т, р, г, и
ф, к, а, а, л, и к, в, о, л а, н, о, о, р, в
к, ж, у ь, о, н, к, у
Это упражнение очень похоже на привычные нам ребусы.
Безусловно, ребус является такой же самой комбинаторной задачей, которая эффективно может использоваться для развития словесно-логического мышления: кроссворды учат ребенка ориентироваться на определение понятия по описанным признакам, задания с числами - устанавливать закономерности, задания с буквами - анализировать и синтезировать различные комбинации. Приведем еще одно подобное упражнение.
Упражнение №21. "Слова-близнецы".
Это упражнение связано с таким явлением русского языка, как омонимия, т.е. когда слова имеют разное значение, но одинаковы по написанию.
"Какое слово обозначает то же самое, что и слова:
1) родник и то, чем открывают дверь;
2) прическу у девочки и инструмент для срезания травы;
3) ветку винограда и инструмент, которым рисуют.
Придумай сам такие слова, которые одинаковы по звучанию, но разные по значению".
Дополнительные задания к упражнению:
4) овощ, от которого плачут, и оружие для стрельбы стрелами (жгучий овощ и стрелковое оружие);
5) часть ружья и часть дерева;
6) то, на чем рисуют, и зелень на ветках;
7) подъемный механизм для стройки и механизм, который нужно открыть, чтобы полилась вода.
Дата: 2018-09-13, просмотров: 959.