6. у = 0; х 2 = 0; х = 0 - нуль функции.
7. 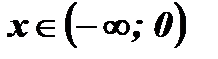 у > 0;
у > 0;
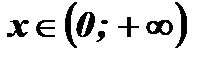 у > 0.
у > 0.
8. Функция является ограниченной снизу, так как у ³ 0.
Замечание: Графиком функции 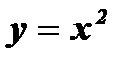 является парабола.
является парабола.
| х |
| у |
| 0 |
| 1 |
| 2 |
| -2 |
| -8 |
| 8 |
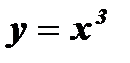 ( a - натуральное нечетное число)
( a - натуральное нечетное число)
1. Область определения функции: 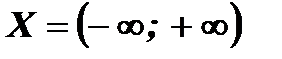
(любое действительное число можно возвести в куб).
2. Множество значений функции: 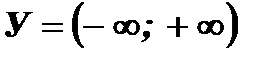 :
:
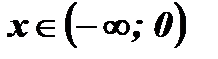
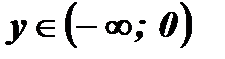 ;
;
х = 0 у = 0;
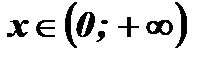
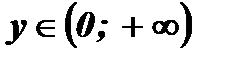 .
.
Вывод: График функции проходит через начало координат, расположен в первой и третьей координатных четвертях.
3. Функция является нечетной, так как ее область определения симметрична относительно начала координат и для любого х Î R выполняется равенство 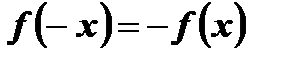 .
.
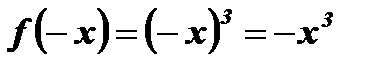 .
.
Вывод: График функции симметричен относительно начала координат.
4. Функция является монотонно возрастающей на всей области определения.
5. Функция 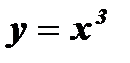 имеет обратную функцию
имеет обратную функцию 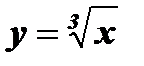 , так как монотонна.
, так как монотонна.
6. у = 0; х 3 = 0; х = 0 - нуль функции.
7. 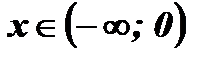 у < 0;
у < 0; 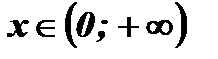 у > 0.
у > 0.
Функция является неограниченной сверху и снизу.
Замечание: Графиком функции 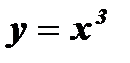 является кубическая парабола.
является кубическая парабола.
Вывод:
1. Функция 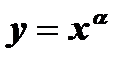 , где a - натуральное четное число, имеет обратную функцию
, где a - натуральное четное число, имеет обратную функцию 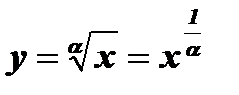 при
при 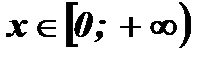 .
.
2. Функция 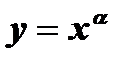 , где a - натуральное нечетное число, имеет обратную функцию
, где a - натуральное нечетное число, имеет обратную функцию 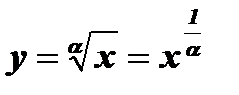 при
при 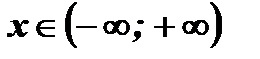 .
.
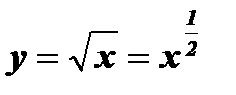 ( a - дробное четное число)
( a - дробное четное число)
1. Область определения функции: 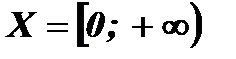 .
.
(Арифметический квадратный корень можно извлечь только из неотрицательного числа).
2. Множество значений функции: 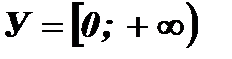 .
.
(При извлечении арифметического квадратного корня из неотрицательного числа получается неотрицательное число).
х = 0 у = 0;
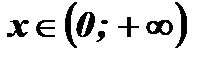
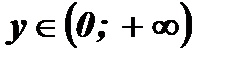 .
.
Вывод: График функции проходит через начало координат, расположен в первой координатной четверти.
3. Функция ни четная, ни нечетная, так как область определения функции не является симметричной относительно начала координат.
Функция является монотонно возрастающей.
Функция обратима, так как монотонна.
6. у = 0; 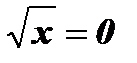 ; х = 0 - нуль функции.
; х = 0 - нуль функции.
7. 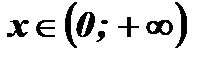 у > 0.
у > 0.
8.
| 0 |
| х |
| у |
| 1 |
| 4 |
| 9 |
| 1 |
| 2 |
| 3 |
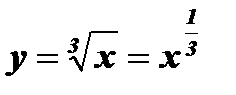 ( a - дробное нечетное число)
( a - дробное нечетное число)
Область определения функции: 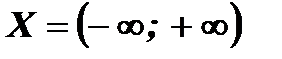 .
.
(Существует корень нечетной степени из отрицательного числа).
1. Множество значений функции: 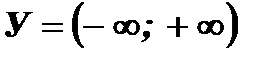 , так как
, так как
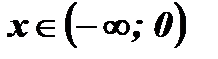
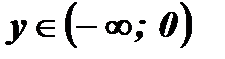 ;
;
х = 0 у = 0;
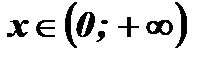
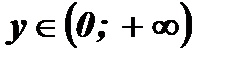 .
.
Вывод: График функции проходит через начало координат, расположен в первой и третьей координатных четвертях.
2. Функция является нечетной, так как ее область определения симметрична относительно начала координат и для любого 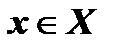 выполняется равенство
выполняется равенство 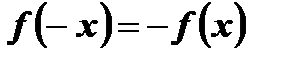 ,
, 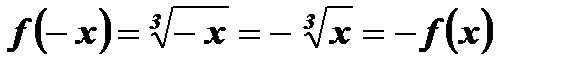 .
.
Вывод: График функции симметричен относительно начала координат.
3. Функция является монотонно возрастающей на всей области определения.
4. Функция 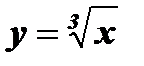 имеет обратную функцию у = х 3, так как монотонна.
имеет обратную функцию у = х 3, так как монотонна.
5. у = 0; 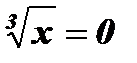 х 3; х = 0 - нуль функции.
х 3; х = 0 - нуль функции.
6. 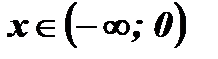 у < 0;
у < 0; 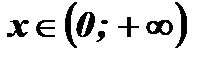 у > 0.
у > 0.
Дата: 2018-12-21, просмотров: 371.