Тема: «Функции, их свойства и графики. Степенная функция»
Степени. Корни.
Определения степеней:
1. an = a × a × … × a, n Î N.
2. a1 = a
3. а 0 = 1 , 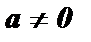 (0 0 - не имеет смысла).
(0 0 - не имеет смысла).
4. 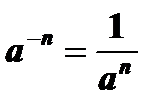 ,
, 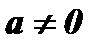 .
.
5. 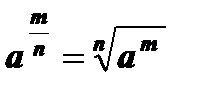 , a³ 0, n Î N , т Î Z.
, a³ 0, n Î N , т Î Z.
Свойства степеней:
Четная степень отрицательного числа есть число положительное.
Нечетная степень отрицательного числа есть число отрицательное.
Любая степень положительного числа есть число положительное.
4. 0 n = 0 , n Î N .
5. 1 n = 1 , n Î N .
6. 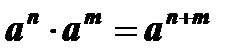 .
.
7. 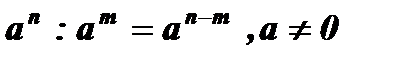 .
.
8. 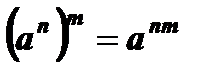 .
.
9. 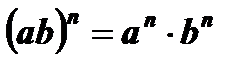 .
.
10. 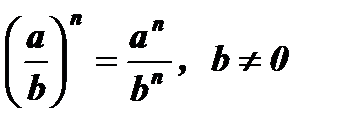 .
.
Определения корней:
1. 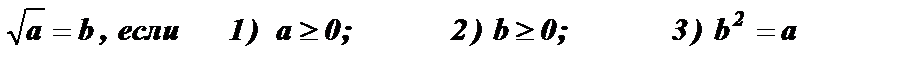 .
.
2. 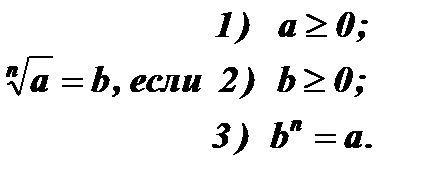
Свойства корней:
1. 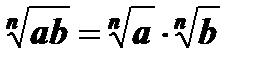 , а ³ 0, b ³ 0.
, а ³ 0, b ³ 0.
2. 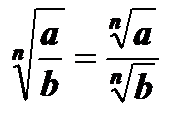 , а ³ 0, b > 0.
, а ³ 0, b > 0.
3. 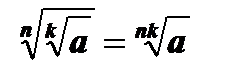 , а ³ 0, n Î N, k Î N.
, а ³ 0, n Î N, k Î N.
4.  , а ³ 0, n Î N, т Î N.
, а ³ 0, n Î N, т Î N.
5. 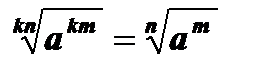 , а ³ 0, n Î N, т Î N , k Î N.
, а ³ 0, n Î N, т Î N , k Î N.
6. При любом значении а 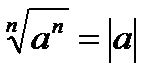 .
.
2. Числовая функция: область определения, множество значений, способы задания
Применение математики к изучению законов природы и к использованию их в технике заставило ввести в математику понятия постоянной и переменной величин. Все величины, изучаемые в математике, делятся на постоянные и переменные.
Определение: Величина называется постоянной, если она в условиях данного эксперимента сохраняет одно и то же значение.
(Постоянная – const. (лат.))
Пример: Постоянными величинами являются:
1. длина радиуса данной окружности;
Температура кипения воды при постоянном давлении.
Замечание: Некоторые постоянные сохраняют свое числовое значение при любых условиях, их называют абсолютными постоянными.
Пример: Абсолютными постоянными величинами являются:
1. сумма углов треугольника;
2. скорость света в пустоте;
3. количество секунд в минуте;
4. p = 3,14…;
5. е = 2,718281828459045… .
Определение: Величина называется переменной, если она в условиях данного эксперимента может принимать различные значения.
Пример: Скорость камня, брошенного вверх, является переменной величиной.
В практических задачах часто рассматриваются переменные величины, которые связаны между собой так, что значения одной определяют значения другой.
Пример: Объем V шара радиуса R определяется по формуле 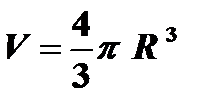 .
.
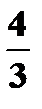 ; p – постоянные величины;
; p – постоянные величины;
R – независимая переменная;
Монотонность функций
Определение: Функция  называется возрастающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее значение функции (Рис. 1).
называется возрастающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее значение функции (Рис. 1).
| у |
| х |
| х2 |
| х1 |
| у2 |
| О |
| у1 |
| х3 |
| у3 |
| у |
| х |
| х2 |
| х1 |
| у2 |
| О |
| у1 |
| х3 |
| у3 |
 называется убывающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует меньшее значение функции. (Рис. 2)
называется убывающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует меньшее значение функции. (Рис. 2)
Рис. 1. Рис. 2
Вывод: График возрастающей функции - восходящая кривая, график убывающей функции - нисходящая кривая при перемещении вдоль оси абсцисс в положительном направлении.
Определение: Функция только возрастающая или только убывающая на данном промежутке называется монотонной на этом промежутке.
| х |
| у |
| О |
| х |
| у |
| О |
| х |
| у |
| О |

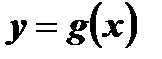
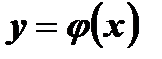
монотонно возрастающая монотонно убывающая не монотонная функция функция функция
Обратимость функций
Определение: Функция называется обратимой (имеет обратную функцию), если она принимает каждое свое значение один раз.
| у |
| х |
| О |
| а |
| b |
| c |
| d |
| х |
| у |
| у |
| х |
| О |
| а |
| b |
| c |
| d |
| х 3 |
| у 1 |
| х 2 |
| х 1 |
Рис. 1:  Рис. 2:
Рис. 2: 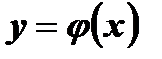
Функции  (Рис. 1) и
(Рис. 1) и 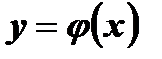 (Рис. 2) определены на
(Рис. 2) определены на 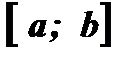 и имеют множество значений
и имеют множество значений 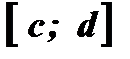 .
.
Функция  принимает каждое свое значение один раз, то есть у = f ( х ) - обратимая функция.
принимает каждое свое значение один раз, то есть у = f ( х ) - обратимая функция.
Функция 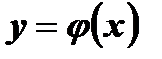 принимает некоторые свои значения не один раз, то есть у = j ( х ) - необратимая функция.
принимает некоторые свои значения не один раз, то есть у = j ( х ) - необратимая функция.
Вывод: Обратима только монотонная функция.
Пример: Найти функцию обратную функции 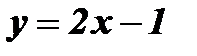 . Построить графики взаимно обратных функций.
. Построить графики взаимно обратных функций.
Решение:
1. Из формулы 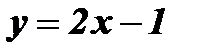 выразим х через у:
выразим х через у: 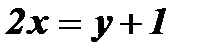 ;
; 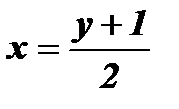 ;
; 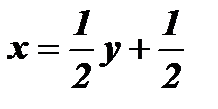 .
.
В полученной формуле поменяем местами х и у: 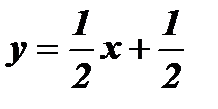 .
.
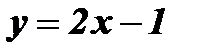 и
и 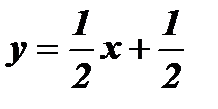 - взаимно обратные функции.
- взаимно обратные функции.
2.
| О |
| х |
| у |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| - 3 |
| - 4 |
| - 5 |
| - 4 |
| - 5 |
| - 2 |
| l1 |
| l2 |
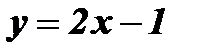 и
и 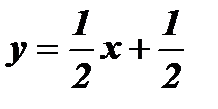 :
:
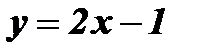 х - 2 2
х - 2 2
у - 5 3
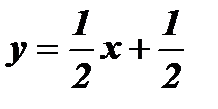
х - 5 3
у - 2 2
График функции 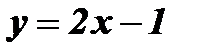 - прямая l1 проходит через точки (- 2; - 5) и (2;3).
- прямая l1 проходит через точки (- 2; - 5) и (2;3).
График функции 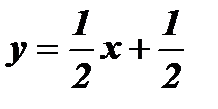 - прямая l2 проходит через точки (- 5; - 2) и (3;2).
- прямая l2 проходит через точки (- 5; - 2) и (3;2).
Прямая 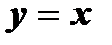 является осью симметрии прямых l1 и l2 .
является осью симметрии прямых l1 и l2 .
Вывод:
1. Чтобы получить функцию, обратную данной функции  , надо из формулы
, надо из формулы  выразить х через у и в полученной формуле поменять местами х и у.
выразить х через у и в полученной формуле поменять местами х и у.
2. Графики взаимно обратных функций симметричны относительно прямой 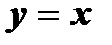 .
.
Ограниченность функций
Определение: Функция  называется ограниченной, если существуют два числа т и М такие, что все значения функции удовлетворяют условию
называется ограниченной, если существуют два числа т и М такие, что все значения функции удовлетворяют условию 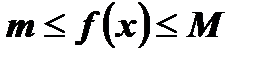 , то есть
, то есть 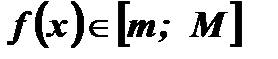 .
.
Определение: Функция  называется ограниченной сверху, если существует число М такое, что все значения функции удовлетворяют условию
называется ограниченной сверху, если существует число М такое, что все значения функции удовлетворяют условию
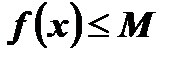 , то есть
, то есть 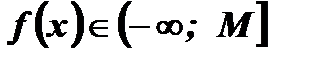 .
.
| х |
| у |
| у |
| х |
| М |
| М |
| т |
 называется ограниченной снизу, если существует число т такое, что все значения функции удовлетворяют условию
называется ограниченной снизу, если существует число т такое, что все значения функции удовлетворяют условию 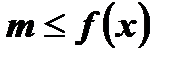 , то есть
, то есть 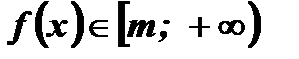 .
.
| у |
| у |
| х |
| х |
| т |
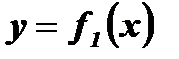 - ограниченная функция
- ограниченная функция 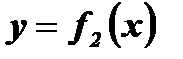 - ограниченная сверху, но неограниченная снизу функция
- ограниченная сверху, но неограниченная снизу функция
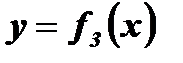 - ограниченная снизу, но
- ограниченная снизу, но 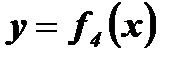 - неограниченнаясверху неограниченная сверху функция и снизу функция
- неограниченнаясверху неограниченная сверху функция и снизу функция
Упражнения:
1. Выяснить, является ли функция четной или нечетной:
а) 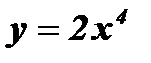 ; б)
; б) 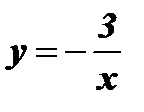 ; в)
; в) 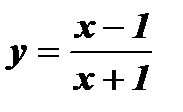 ; г)
; г) 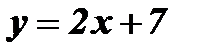 ;
;
2. Найти область определения функции, заданной формулой:
U AAYACAAAACEAndLTfpAKAAAyVgAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwEC LQAUAAYACAAAACEAAnn+zuEAAAAKAQAADwAAAAAAAAAAAAAAAADqDAAAZHJzL2Rvd25yZXYueG1s UEsFBgAAAAAEAAQA8wAAAPgNAAAAAA== ">
| х |
| у |
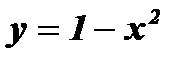 ; б)
; б) 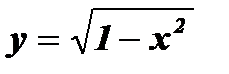 ; в)
; в) 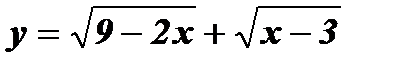 .
.
3. Дана функция 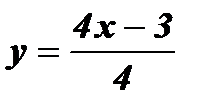 на отрезке
на отрезке 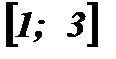 .
.
Найти обратную ей функцию и ее область определения.
4. Исследовать функцию, заданную графиком:
Схема исследования функции
- Область определения функции.
- Множество значений функции.
- Четность, нечетность функции.
- Монотонность функции.
- Обратимость функции.
- Нули функции.
- Промежутки знакопостоянства функции.
- Ограниченность функции.
4. Линейная функция, ее свойства и графики
Определение: Линейной функцией называется функция вида 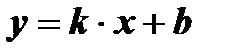 , где x – независимая переменная, k, b – некоторые числа.
, где x – независимая переменная, k, b – некоторые числа.
Замечание: Графиком линейной функции является прямая.
1. Область определения функции 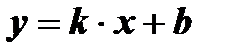 :
: 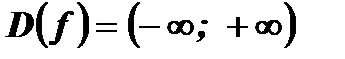 .
.
2. Множество значений функции 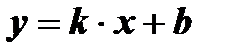 :
: 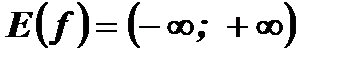 .
.
3. Функция 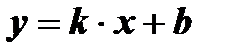 не является ни четной, ни нечетной, так как
не является ни четной, ни нечетной, так как
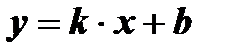 ;
; 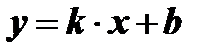 f ( - х ) = k ∙ ( - х ) + b = - k ∙ x + b;
f ( - х ) = k ∙ ( - х ) + b = - k ∙ x + b;
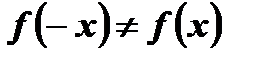 и
и 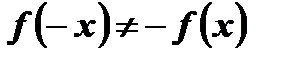 .
.
4.
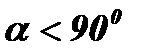
|
| х |
| 0 |
| у |
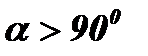
|
| х |
| 0 |
| у |
| l |
| l |
Рис. 1. Рис. 2.
Определение: Угловым коэффициентом прямой называется тангенс угла наклона прямой к положительному направлению оси абсцисс.
a - угол наклона прямой l к положительному направлению оси Ох.
k = tg a - угловой коэффициент прямой l .
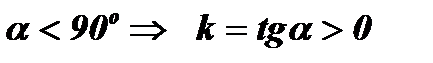 Þ
Þ 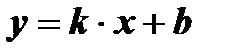 – монотонно возрастающая функция (Рис. 1.)
– монотонно возрастающая функция (Рис. 1.)
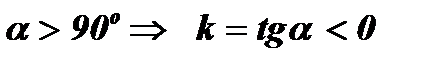 Þ
Þ 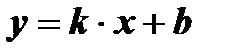 – монотонно убывающая функция (Рис. 2.)
– монотонно убывающая функция (Рис. 2.)
5. Функция 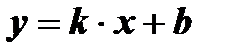 является обратимой:
является обратимой:
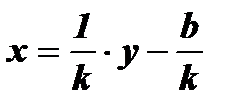 ;
; 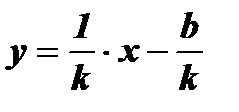 - функция, обратная для
- функция, обратная для 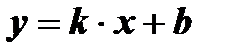 .
.
6.
| __ |
| х |
| + |
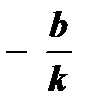
|
| __ |
| х |
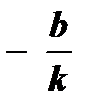
|
| + |
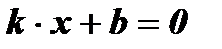 ;
; 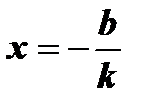 - нуль функции
- нуль функции 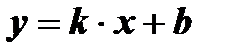 ( k ¹ 0 ).
( k ¹ 0 ).
7.
Рис. 3. Рис. 4.
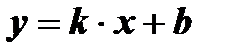 ;
; 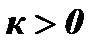 ;
; 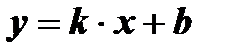 ;
; 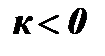 ;
;
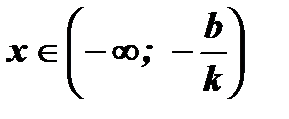 y < 0;
y < 0; 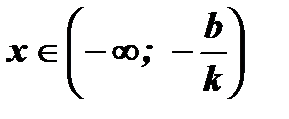 y > 0;
y > 0;
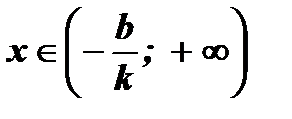 y > 0.
y > 0. 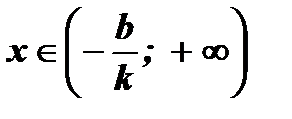 y < 0 .
y < 0 .
8. Функция неограниченная: 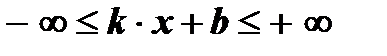
9. При х = 0 у = b.
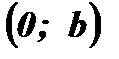 – точка пересечения прямой с осью Оу.
– точка пересечения прямой с осью Оу.
b – начальная ордината – отрезок, отсекаемый прямой на оси Оу .
| х |
| 0 |
| у |
| b > 0 |
| (0; b) |
| х |
| 0 |
| у |
| b < 0 |
| (0; b) |
Рис. 5. Рис. 6.
Частные случаи линейной функции 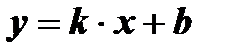 .
.
1. k = 0; y = b ( у = const );
2. b = 0, k ¹ 0; y = k x – прямая пропорциональность.
Пример:
х
О
у
1
- 2
1
a
х
О
у
1
- 1
1
a
- 1
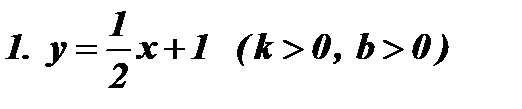
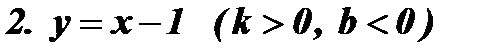
Рис.1 Рис. 2
| х |
| О |
| у |
| 1 |
| - 1 |
| 1 |
| a |
| 2 |
| 2 |
| х |
| О |
| у |
| - 2 |
| 1 |
| a |
| - 1 |
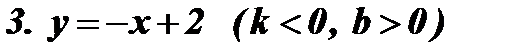
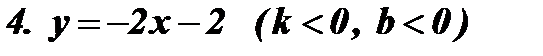
Рис. 3 Рис. 4
| х |
| 0 |
| у |
| 1 |
| - 1 |
| 1 |
| у = 0, a = 0 |
| х |
| 0 |
| 3 |
| 1 |
| a |
| - 1 |
| у |
| 1 |
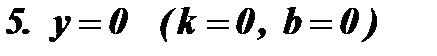
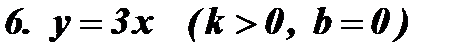
Рис. 5 Рис. 6
5. Степенная функция, ее свойства и графики
Определение: Функция вида 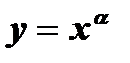 , где a Î R, называется степенной функцией.
, где a Î R, называется степенной функцией.
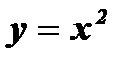 ( a - натуральное четное число)
( a - натуральное четное число)
1. Область определения функции: 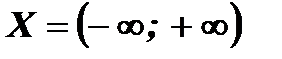 (любое действительное число можно возвести в квадрат).
(любое действительное число можно возвести в квадрат).
2. Множество значений функции: 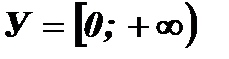
(при возведении в квадрат любого действительного числа получается неотрицательное число).
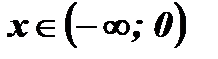
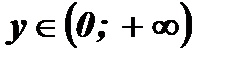 ;
;
х = 0 у = 0;
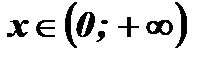
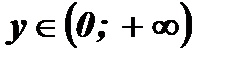 .
.
| х |
| у |
| 0 |
| 1 |
| 2 |
| 3 |
| -1 |
| -2 |
| -3 |
| 1 |
| 4 |
| 9 |
3. Функция является четной, так как ее область определения симметрична относительно начала координат и для любого х Î R выполняется равенство 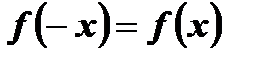 .
.
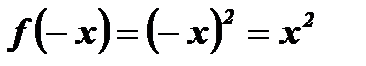 .
.
Вывод: График функции симметричен относительно оси ординат.
4. Функция не является монотонной, так как она убывает при 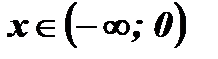 и возрастает при
и возрастает при 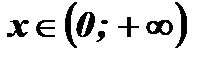 .
.
Рис. 1 Рис. 2 Рис. 3
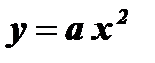 ( b = 0, c = 0)
( b = 0, c = 0) 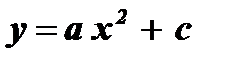 ( b = 0)
( b = 0) 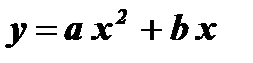 ( c = 0)
( c = 0)
Общий случай: 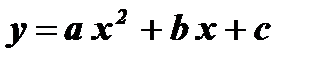 ( b ¹ 0, c ¹ 0)
( b ¹ 0, c ¹ 0)
- Область определения функции: Х = R.
- Координаты вершины параболы А ( т, п ) определяются по формулам:
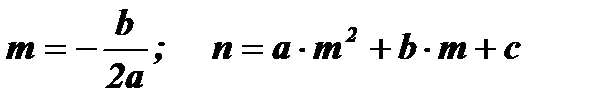 .
.
- Множество значений функции: при а > 0
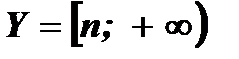 ;
;
при а < 0 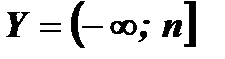 .
.
- Функция ни четная ни нечетная, так как
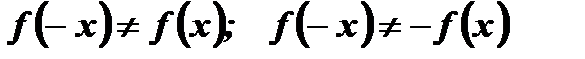 .
.
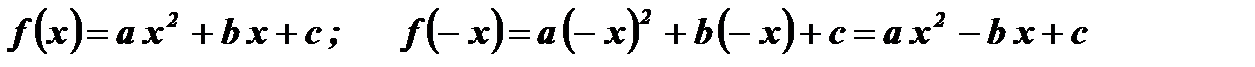 .
.
| х |
| у |
| 0 |
| т |
| п |
| т |
| п |
| т |
| т |
| п |
| п |
| у |
| х |
| 0 |
Рис. 4 Рис. 5
а > 0, b ¹ 0, c ¹ 0 а < 0, b ¹ 0, c ¹ 0
- Функция не монотонная:
при а > 0 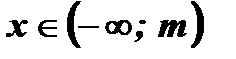 у - убывает;
у - убывает;
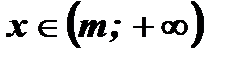 у - возрастает;
у - возрастает;
при а < 0 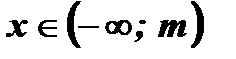 у - возрастает;
у - возрастает;
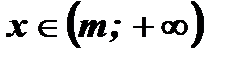 у - убывает.
у - убывает.
- Функция не обратимая, так как не монотонная.
- Нули функции:
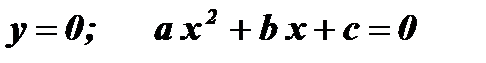 ;
;
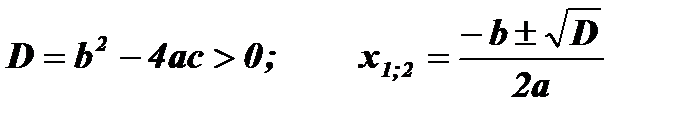 ; х1;2 - нули функции;
; х1;2 - нули функции;
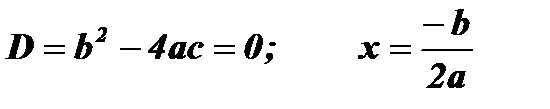 ; х - нуль функции;
; х - нуль функции;
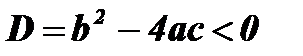 ; нулей функции нет.
; нулей функции нет.
- Промежутки знакопостоянства:
| х |
| х |
| х |
| х1 |
| х2 |
| х |
| + |
| + |
| - |
| + |
| + |
| + |
| + |
| + |
Рис. 5 Рис. 6 Рис. 7
а > 0; D > 0; а > 0; D = 0; а > 0; D < 0;
| х |
| х |
| х |
| х1 |
| х2 |
| х |
| + |
| - |
| - |
| - |
| - |
| - |
| - |
| - |
Рис. 8 Рис. 9 Рис. 10
а < 0; D > 0; а < 0; D = 0; а < 0; D < 0;
- При
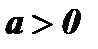 функция ограниченная снизу, так как
функция ограниченная снизу, так как 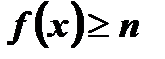 при любом
при любом 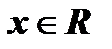 ; при
; при 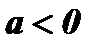 функция ограниченная сверху, так как
функция ограниченная сверху, так как 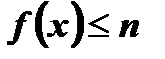 при любом
при любом 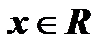 .
.
7. Уравнения с одной переменной
7.1. Уравнения, содержащие переменную под знаком модуля.
Определение: Модулем (абсолютной величиной) действительного числа а называется само число а, если 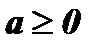 , и противоположное число - а, если
, и противоположное число - а, если 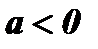 .
.
Обозначение:  - модуль числа а.
- модуль числа а.
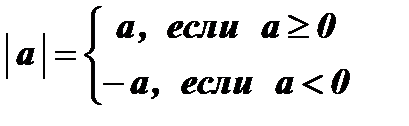
Замечание:
1. Из определения следует, что при любом действительном а 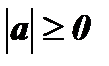 .
.
2. Модуль числа равен расстоянию от точки, изображающей данное действительное число на числовой оси, до нуля.
| 2 |
| - 2 |
| 0 |
| 1 |
| 3,5 |
| х |
| - 1 |
| 3 |
| 4 |
| ½2 ½ |
| ½ - 2 ½ |
| ½3,5 ½ |
| ½0 ½ |
½ - 2 ½= 2; ½2 ½= 2; ½3,5 ½= 3,5; ½0 ½= 0.
3. ½b - а½ - расстояние между точками, изображающими на числовой оси числа а и b .
| 0 |
| a |
| х |
| ½ b ½ |
| ½ a ½ |
| ½ b - a ½ |
| b |
| 0 |
| b |
| х |
| ½а ½ |
| ½ b ½ |
| ½ b - a ½ |
| a |
½b - а½= b - а , если b > а ½b - а½= а - b , если b < а
Способы решения уравнений, содержащих переменную под знаком модуля:
1. Раскрытие модуля по определению.
2. Возведение обеих частей уравнения в квадрат.
3. Разбиение на промежутки.
Пример:
1. 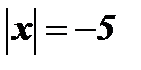 .
.
Решение:
Так как при любом х 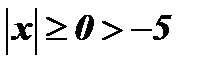 , то уравнение решений не имеет.
, то уравнение решений не имеет.
Ответ: Решений нет.
2. 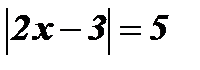 .
.
Решение:
Раскроем 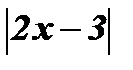 по определению:
по определению:
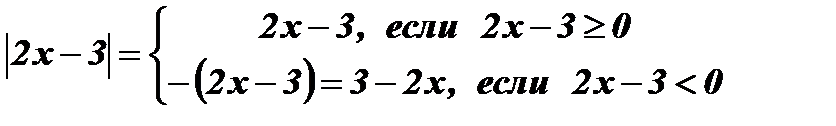
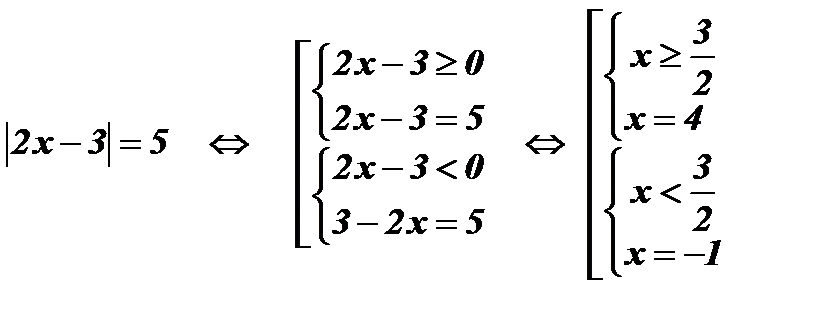
Ответ: х1 = 4; х2 = - 1 .
Теорема: Если обе части уравнения 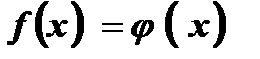 , где
, где 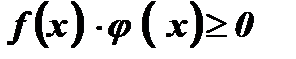 при всех значениях х из области определения уравнения, возвести в одну и ту же натуральную степень п , то получится уравнение
при всех значениях х из области определения уравнения, возвести в одну и ту же натуральную степень п , то получится уравнение 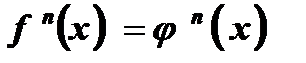 , равносильное данному.
, равносильное данному.
3. 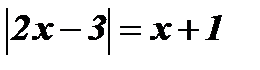 .
.
Решение:
Если х+1 < 0 , то уравнение корней не имеет, так как 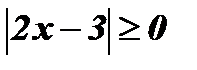 .
.
Если х+1 ≥ 0 , то обе части уравнения неотрицательны, возведем их в квадрат:
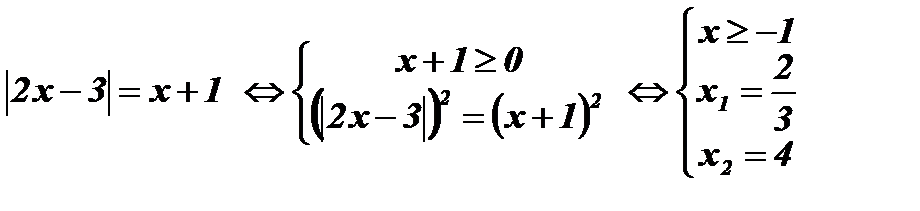
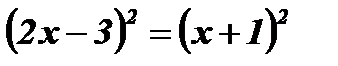 ;
; 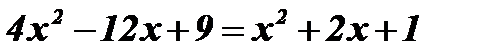 ;
; 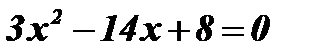 ;
;
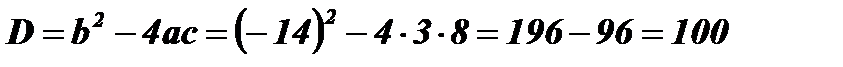 ;
;
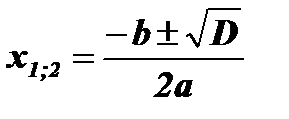 ;
; 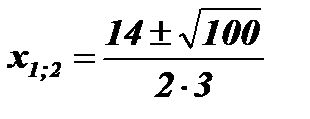 ;
; 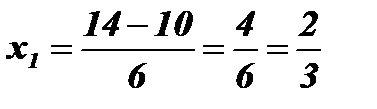 ;
; 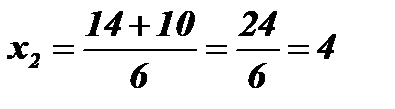 .
.
Ответ:  ;
; 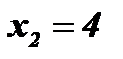 .
.
4. 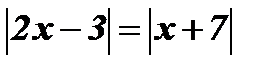 .
.
Решение:
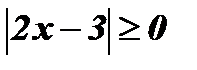 ,
, 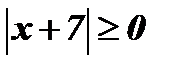 .
.
Так как обе части уравнения положительны, возведем их в квадрат:
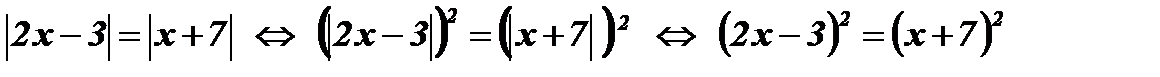 Û
Û
Û 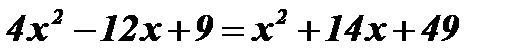 Û
Û 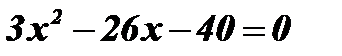 ;
;
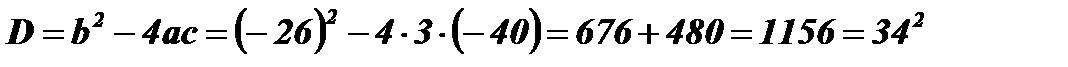 ;
;
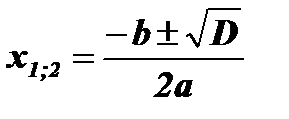 ;
; 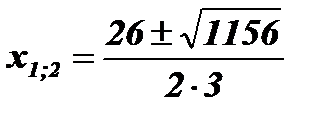 ;
;
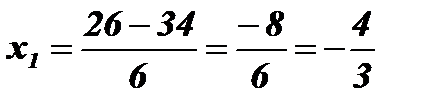 ;
; 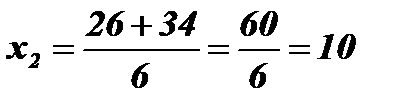 .
.
Ответ: 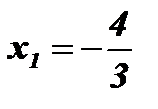 ;
; 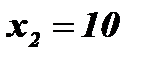 .
.
5. 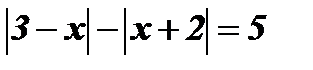 .
.
Решение:
1) На числовой прямой отметим значения х, при которых 3 – х = 0, и значения х, при которых х + 2 = 0.
3 – х = 0 при х = 3.
х + 2 = 0 при х = – 2.
2) Числовая прямая разбивается на промежутки: 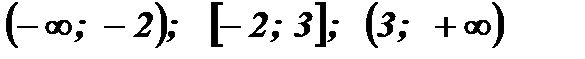 .
.
Определим знак каждого из двучленов в полученных промежутках:
| 3 |
| 3 – х |
| х |
| х +2 |
| - 2 |
| + |
| + |
| - |
| - |
| + |
| + |
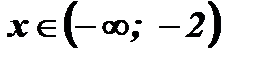
| 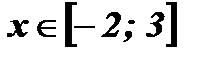
| 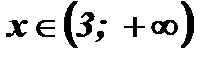
| |
| 3 – х | + | + | - |
| х +2 | - | + | + |
3) Решим уравнение на каждом промежутке:
При 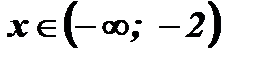
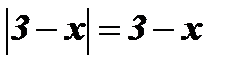 ;
; 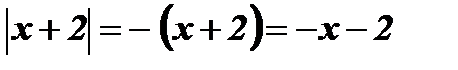 .
.
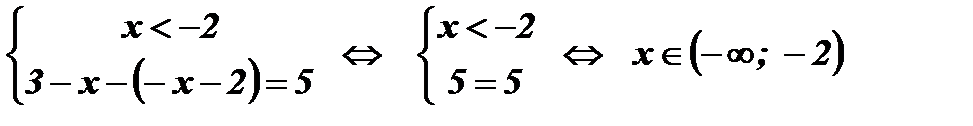 .
.
При 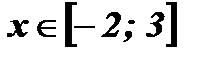
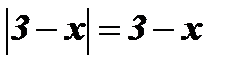 ;
; 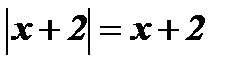 .
.
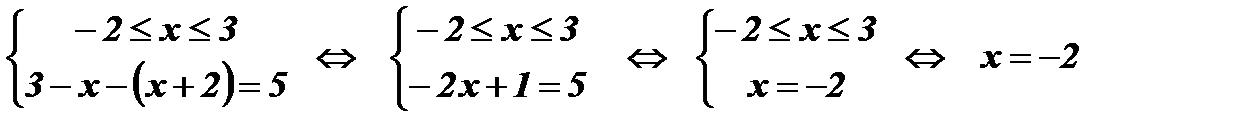 .
.
При 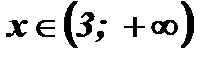
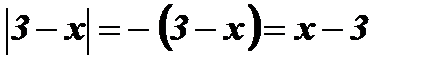 ;
; 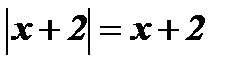 .
.
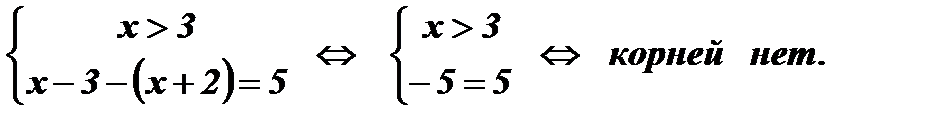
Ответ: 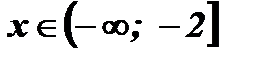 .
.
Упражнения:
1. 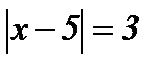 ; ;
| 2. 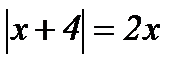 ; ;
| 3. 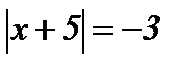 ; ;
|
4. 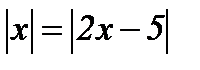 ; ;
| 5. 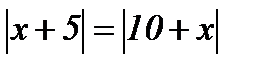 ; ;
| 6. 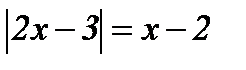 ; ;
|
7. 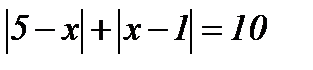 ; ;
| 8. 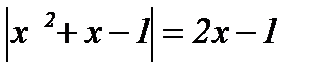 ; ;
| 9. 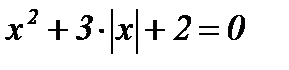 ; ;
|
10. 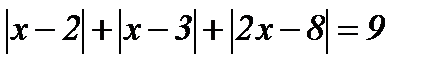 ; ;
| 11. 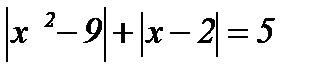 ; ;
| 12. 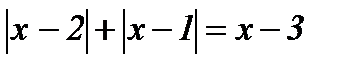 ; ;
|
13. 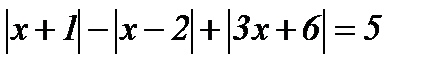 ; ;
| 14. 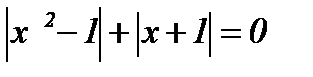 ; ;
| 15. 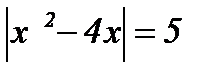 . .
|
7.2. Иррациональные уравнения
Определение: Иррациональным уравнением называется уравнение, содержащее переменную под знаком корня или под знаком операции возведения в дробную степень.
Замечание: Чтобы решить иррациональное уравнение, нужно сначала освободиться от корней, подкоренные выражения которых содержат переменную. Чаще всего этого добиваются возведением в квадрат обеих частей уравнения. Однако при этом могут появиться «посторонние» корни, которые не удовлетворяют данному иррациональному уравнению. Появление «посторонних» корней возможно при расширении области определения данного иррационального уравнения.
Вывод: При решении иррациональных уравнений необходима проверка.
Пример:
-
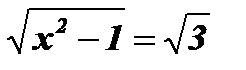 .
.
Решение:
Возведем обе части уравнения в квадрат: 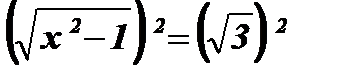 ;
;
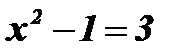 ;
; 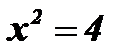 ;
; 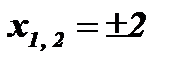 .
.
Проверка:
х1 = 2; 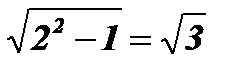 ;
; 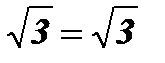 ;
;
х2 = - 2; 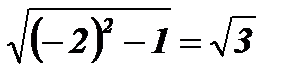 ;
; 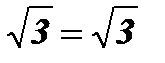 .
.
Ответ: 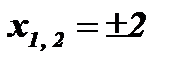 .
.
-
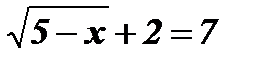 .
.
Решение:
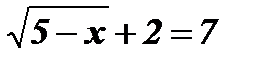 Û
Û 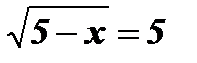 ;
;
Возведем обе части уравнения в квадрат: 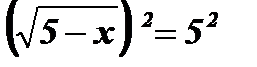 ; 5 - х = 25; х = - 20.
; 5 - х = 25; х = - 20.
Проверка:
х = - 20; 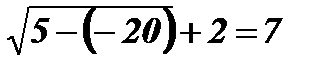 ; 7 = 7.
; 7 = 7.
Ответ: х = - 20.
-
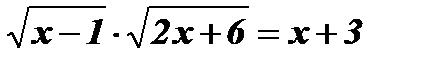 .
.
Решение:
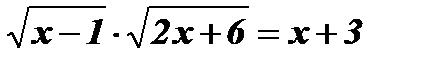 Û
Û 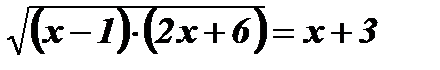 Û
Û 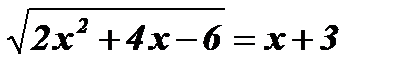 ;
;
Возведем обе части уравнения в квадрат: 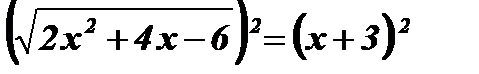 ;
;
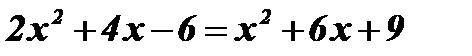 ;
; 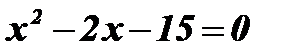 ;
;
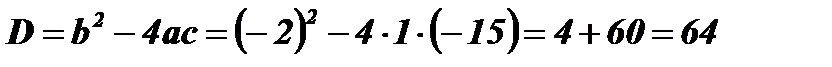 ;
;
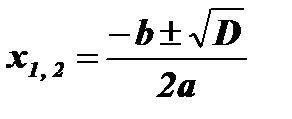 ;
; 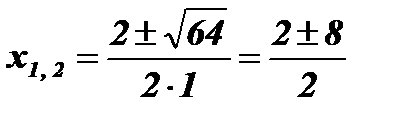 ; х1 = - 3; х2 = 5.
; х1 = - 3; х2 = 5.
Проверка:
х1 = - 3; 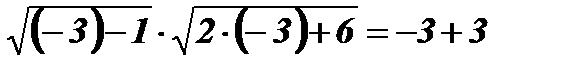 ;
; 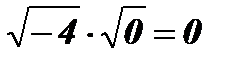 ;
; 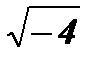 - не существует;
- не существует;
х1 = - 3 - не является корнем данного уравнения.
х2 = 5; 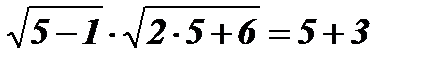 ; 8 = 8.
; 8 = 8.
Ответ: х = 5.
-
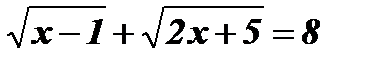 .
.
Решение:
Возведем обе части уравнения в квадрат: 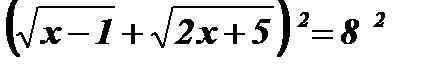 ;
;
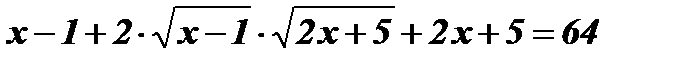 ;
; 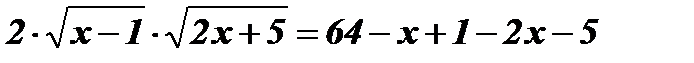 ;
;
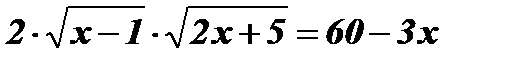 ;
;
Возведем обе части уравнения в квадрат: 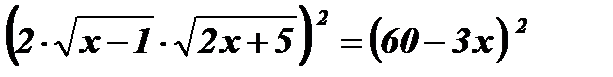 ;
;
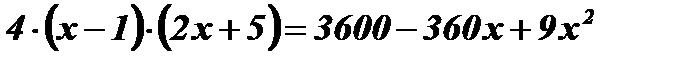 ;
; 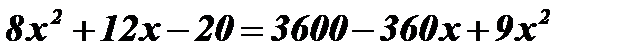 ;
;
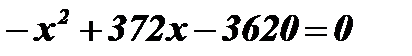 ;
;
Умножим обе части уравнения на - 1: 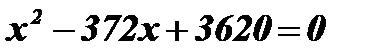 ;
;
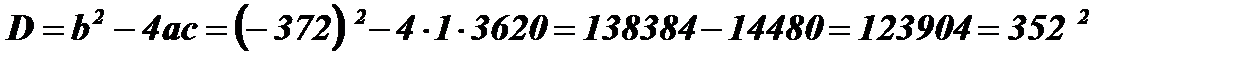 ;
;
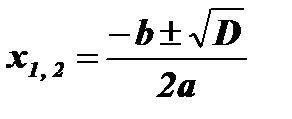 ;
; 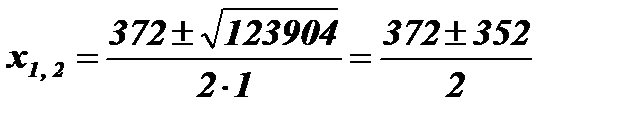 ; х1 = 10; х2 = 362.
; х1 = 10; х2 = 362.
Проверка:
х1 = 10; 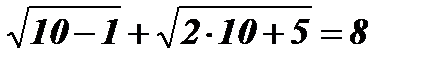 ; 8 = 8.
; 8 = 8.
х2 = 362; 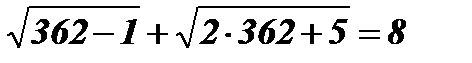 ; 19 + 27 ¹ 8.
; 19 + 27 ¹ 8.
х2 = 362 - не является корнем данного иррационального уравнения.
Ответ: х = 10.
-
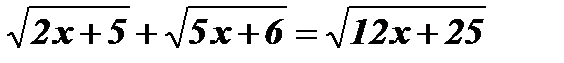 .
.
Решение:
Возведем обе части уравнения в квадрат: 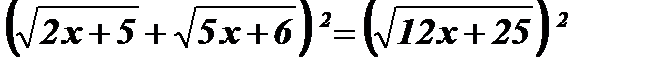 ;
;
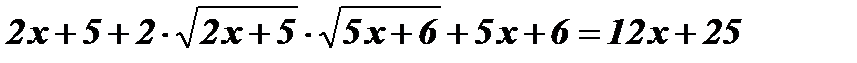 ;
; 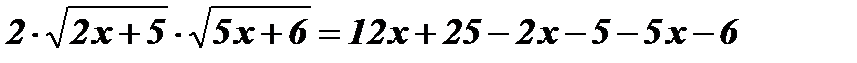 ;
;
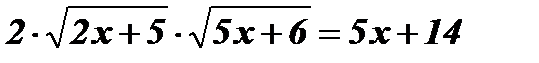 ;
;
Возведем обе части уравнения в квадрат: 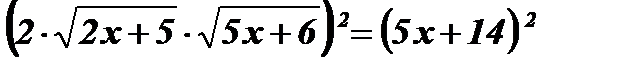 ;
;
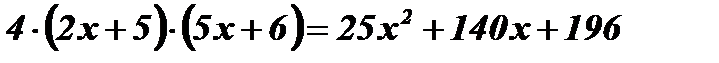 ;
; 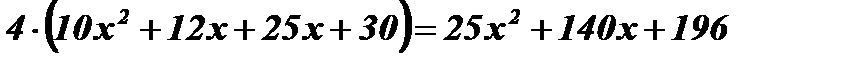 ;
;
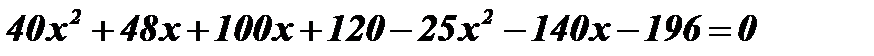 ;
; 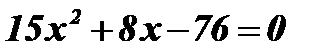 ;
;
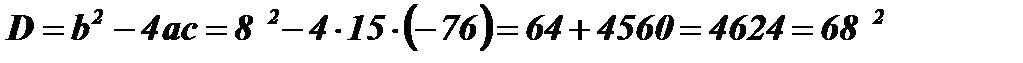 ;
;
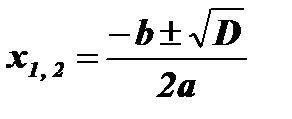 ;
; 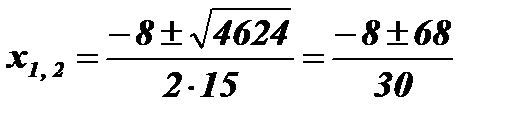 ; х1 = 2; х2 =
; х1 = 2; х2 = 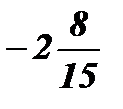 .
.
Проверка:
х1 = 2; 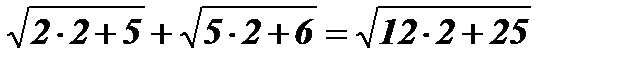 ; 3 + 4 = 7; 7 = 7.
; 3 + 4 = 7; 7 = 7.
х2 = 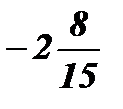 ;
; 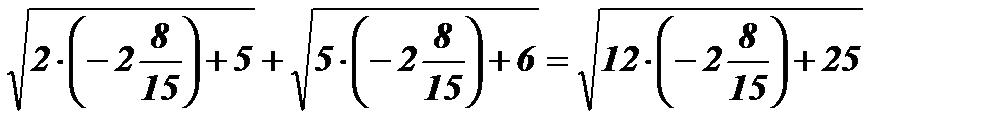 ;
;
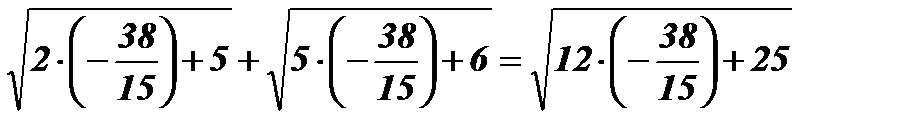 ;
;
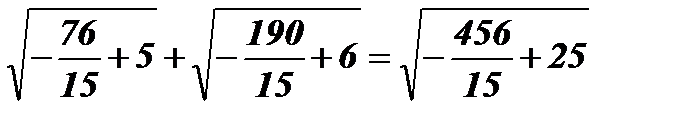 ;
; 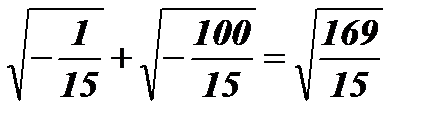 ;
;
Тема: «Функции, их свойства и графики. Степенная функция»
Степени. Корни.
Определения степеней:
1. an = a × a × … × a, n Î N.
2. a1 = a
3. а 0 = 1 , 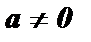 (0 0 - не имеет смысла).
(0 0 - не имеет смысла).
4. 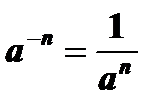 ,
, 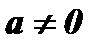 .
.
5. 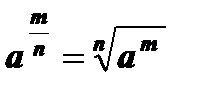 , a³ 0, n Î N , т Î Z.
, a³ 0, n Î N , т Î Z.
Свойства степеней:
Дата: 2018-12-21, просмотров: 481.