Определение: Функция  называется четной, если она обладает следующими свойствами:
называется четной, если она обладает следующими свойствами:
1) область определения этой функции симметрична относительно начала координат, то есть 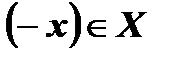 для любого
для любого 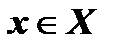 ;
;
2) для любого значения х, принадлежащего области определения этой функции, выполняется равенство 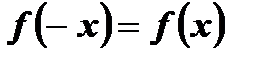 .
.
Вывод:
1. Если точка 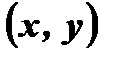 принадлежит графику четной функции, то точка
принадлежит графику четной функции, то точка 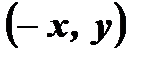 так же принадлежит графику этой функции.
так же принадлежит графику этой функции.
2.
Так как любая пара точек 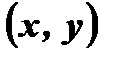 и
и 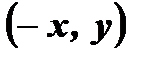 , принадлежащих графику четной функции, симметрична относительно оси ординат, следовательно, график любой четной функции симметричен относительно оси ординат (Рис. 1).
, принадлежащих графику четной функции, симметрична относительно оси ординат, следовательно, график любой четной функции симметричен относительно оси ординат (Рис. 1).
Рис. 1. Рис. 2.
Пример: 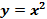 – четная функция, так как , во-первых, область определения этой функции
– четная функция, так как , во-первых, область определения этой функции 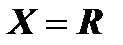 симметрична относительно начала координат; во-вторых, для любого
симметрична относительно начала координат; во-вторых, для любого 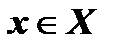 выполняется равенство
выполняется равенство 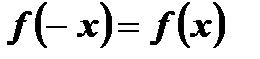 .
.
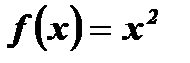 ,
, 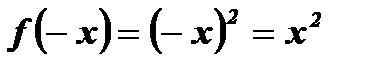 (Рис. 2).
(Рис. 2).
Определение: Функция  называется нечетной, если она обладает следующими свойствами:
называется нечетной, если она обладает следующими свойствами:
1) область определения этой функции симметрична относительно начала координат, то есть 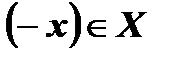 для любого
для любого 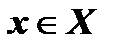 ;
;
2)
для любого значения х, принадлежащего области определения этой функции, выполняется равенство 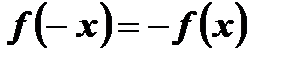 .
.
Вывод:
1. Если точка 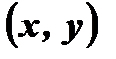 принадлежит графику нечетной функции, то точка
принадлежит графику нечетной функции, то точка 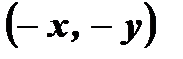 так же принадлежит графику этой функции.
так же принадлежит графику этой функции.
2. Так как любая пара точек 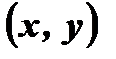 и
и 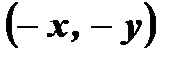 , принадлежащих графику нечетной функции, симметрична относительно начала координат, следовательно, график любой нечетной функции симметричен относительно начала координат.
, принадлежащих графику нечетной функции, симметрична относительно начала координат, следовательно, график любой нечетной функции симметричен относительно начала координат.
Пример: 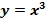 – нечетная функция, так как , во-первых, область определения этой функции
– нечетная функция, так как , во-первых, область определения этой функции  симметрична относительно начала координат; во-вторых, для любого
симметрична относительно начала координат; во-вторых, для любого 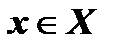 выполняется равенство
выполняется равенство 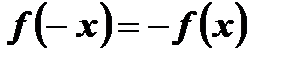 .
.
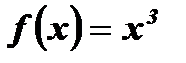 ,
, 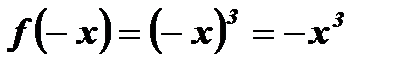 .
.
Пример: Исследовать на четность и нечетность функции:
1) 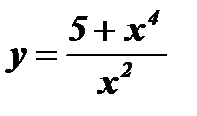 ;
;
Область определения данной функции 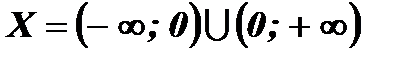 симметрична относительно начала координат. Найдем
симметрична относительно начала координат. Найдем 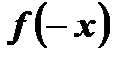 и сравним с
и сравним с 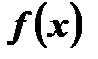 :
: 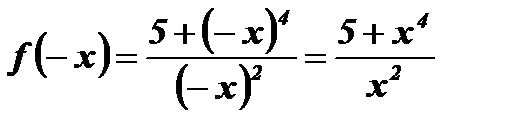 ,
, 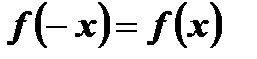 .
.
Следовательно, 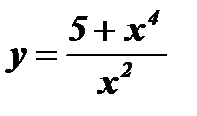 является четной функцией.
является четной функцией.
2) 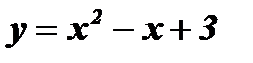 ;
;
Область определения данной функции 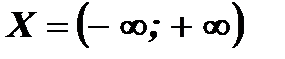 симметрична относительно начала координат. Найдем
симметрична относительно начала координат. Найдем 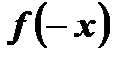 и сравним с
и сравним с 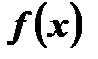 :
:
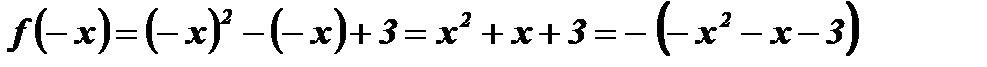 ,
,
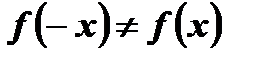 и
и 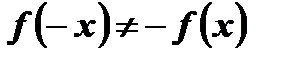 . Следовательно,
. Следовательно, 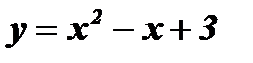 не является ни четной, ни нечетной функцией.
не является ни четной, ни нечетной функцией.
3) 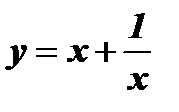 .
.
Область определения данной функции 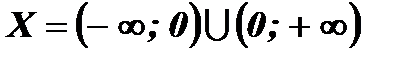 симметрична относительно начала координат. Найдем
симметрична относительно начала координат. Найдем 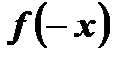 и сравним с
и сравним с 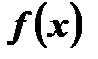 :
: 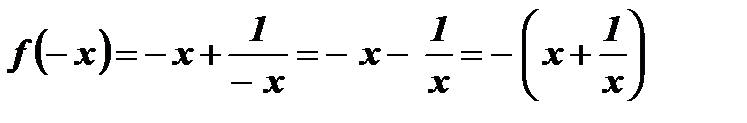 ,
, 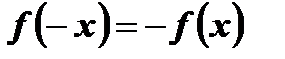 .
.
Следовательно, 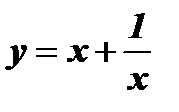 является нечетной функцией.
является нечетной функцией.
Монотонность функций
Определение: Функция  называется возрастающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее значение функции (Рис. 1).
называется возрастающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее значение функции (Рис. 1).
Определение: Функция  называется убывающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует меньшее значение функции. (Рис. 2)
называется убывающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует меньшее значение функции. (Рис. 2)
Рис. 1. Рис. 2
Вывод: График возрастающей функции - восходящая кривая, график убывающей функции - нисходящая кривая при перемещении вдоль оси абсцисс в положительном направлении.
Определение: Функция только возрастающая или только убывающая на данном промежутке называется монотонной на этом промежутке.

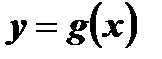
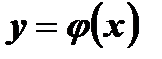
монотонно возрастающая монотонно убывающая не монотонная функция функция функция
Обратимость функций
Определение: Функция называется обратимой (имеет обратную функцию), если она принимает каждое свое значение один раз.
Рис. 1:  Рис. 2:
Рис. 2: 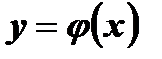
Функции  (Рис. 1) и
(Рис. 1) и 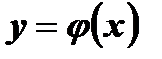 (Рис. 2) определены на
(Рис. 2) определены на 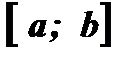 и имеют множество значений
и имеют множество значений 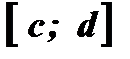 .
.
Функция  принимает каждое свое значение один раз, то есть у = f ( х ) - обратимая функция.
принимает каждое свое значение один раз, то есть у = f ( х ) - обратимая функция.
Функция 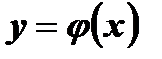 принимает некоторые свои значения не один раз, то есть у = j ( х ) - необратимая функция.
принимает некоторые свои значения не один раз, то есть у = j ( х ) - необратимая функция.
Вывод: Обратима только монотонная функция.
Пример: Найти функцию обратную функции 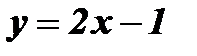 . Построить графики взаимно обратных функций.
. Построить графики взаимно обратных функций.
Решение:
1. Из формулы 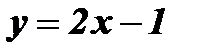 выразим х через у:
выразим х через у: 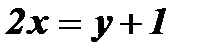 ;
; 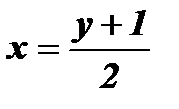 ;
; 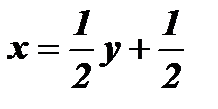 .
.
В полученной формуле поменяем местами х и у: 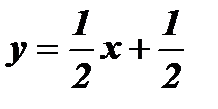 .
.
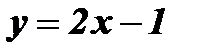 и
и 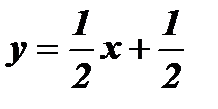 - взаимно обратные функции.
- взаимно обратные функции.
2.
Построим графики взаимно обратных функций 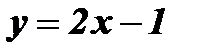 и
и 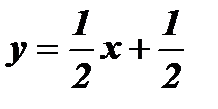 :
:
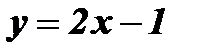 х - 2 2
х - 2 2
у - 5 3
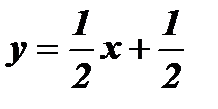
х - 5 3
у - 2 2
График функции 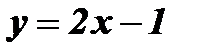 - прямая l1 проходит через точки (- 2; - 5) и (2;3).
- прямая l1 проходит через точки (- 2; - 5) и (2;3).
График функции 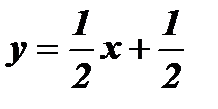 - прямая l2 проходит через точки (- 5; - 2) и (3;2).
- прямая l2 проходит через точки (- 5; - 2) и (3;2).
Прямая 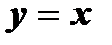 является осью симметрии прямых l1 и l2 .
является осью симметрии прямых l1 и l2 .
Вывод:
1. Чтобы получить функцию, обратную данной функции  , надо из формулы
, надо из формулы  выразить х через у и в полученной формуле поменять местами х и у.
выразить х через у и в полученной формуле поменять местами х и у.
2. Графики взаимно обратных функций симметричны относительно прямой 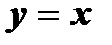 .
.
 называется четной, если она обладает следующими свойствами:
называется четной, если она обладает следующими свойствами: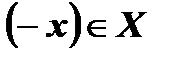 для любого
для любого 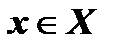 ;
;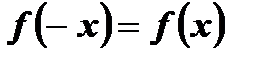 .
. 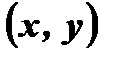 принадлежит графику четной функции, то точка
принадлежит графику четной функции, то точка 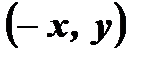 так же принадлежит графику этой функции.
так же принадлежит графику этой функции.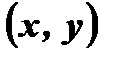 и
и 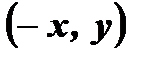 , принадлежащих графику четной функции, симметрична относительно оси ординат, следовательно, график любой четной функции симметричен относительно оси ординат (Рис. 1).
, принадлежащих графику четной функции, симметрична относительно оси ординат, следовательно, график любой четной функции симметричен относительно оси ординат (Рис. 1).
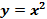 – четная функция, так как , во-первых, область определения этой функции
– четная функция, так как , во-первых, область определения этой функции 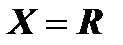 симметрична относительно начала координат; во-вторых, для любого
симметрична относительно начала координат; во-вторых, для любого 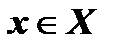 выполняется равенство
выполняется равенство 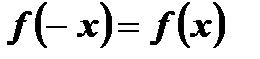 .
. 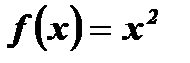 ,
, 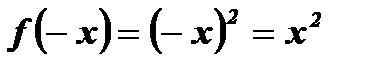 (Рис. 2).
(Рис. 2). называется нечетной, если она обладает следующими свойствами:
называется нечетной, если она обладает следующими свойствами: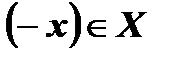 для любого
для любого 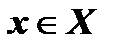 ;
;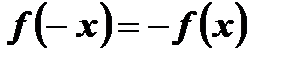 .
.
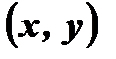 принадлежит графику нечетной функции, то точка
принадлежит графику нечетной функции, то точка 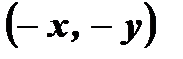 так же принадлежит графику этой функции.
так же принадлежит графику этой функции.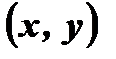 и
и 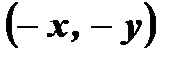 , принадлежащих графику нечетной функции, симметрична относительно начала координат, следовательно, график любой нечетной функции симметричен относительно начала координат.
, принадлежащих графику нечетной функции, симметрична относительно начала координат, следовательно, график любой нечетной функции симметричен относительно начала координат.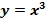 – нечетная функция, так как , во-первых, область определения этой функции
– нечетная функция, так как , во-первых, область определения этой функции  симметрична относительно начала координат; во-вторых, для любого
симметрична относительно начала координат; во-вторых, для любого 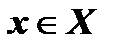 выполняется равенство
выполняется равенство 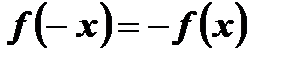 .
. 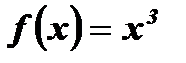 ,
, 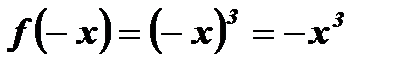 .
.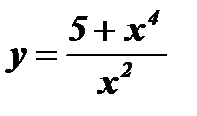 ;
;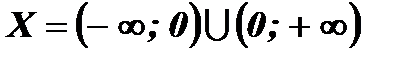 симметрична относительно начала координат. Найдем
симметрична относительно начала координат. Найдем 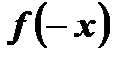 и сравним с
и сравним с 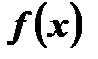 :
: 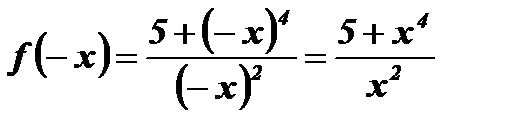 ,
, 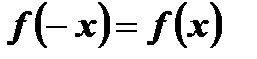 .
.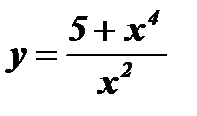 является четной функцией.
является четной функцией.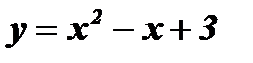 ;
;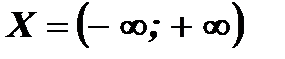 симметрична относительно начала координат. Найдем
симметрична относительно начала координат. Найдем 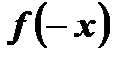 и сравним с
и сравним с 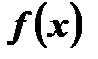 :
: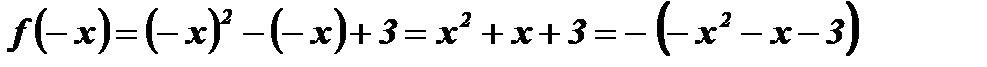 ,
,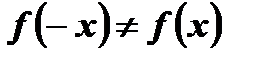 и
и 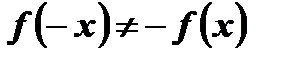 . Следовательно,
. Следовательно, 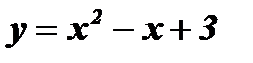 не является ни четной, ни нечетной функцией.
не является ни четной, ни нечетной функцией.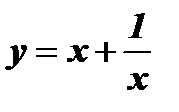 .
.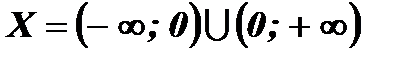 симметрична относительно начала координат. Найдем
симметрична относительно начала координат. Найдем 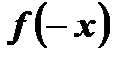 и сравним с
и сравним с 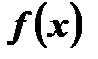 :
: 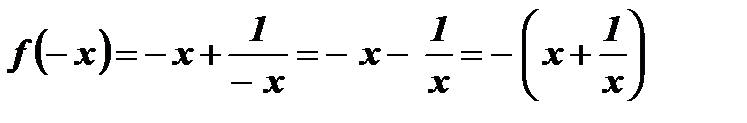 ,
, 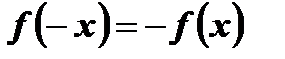 .
.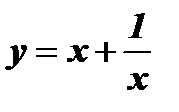 является нечетной функцией.
является нечетной функцией. называется возрастающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее значение функции (Рис. 1).
называется возрастающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее значение функции (Рис. 1). называется убывающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует меньшее значение функции. (Рис. 2)
называется убывающей на промежутке Х, если большему значению аргумента из этого промежутка соответствует меньшее значение функции. (Рис. 2)

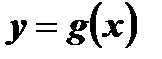
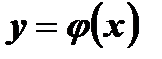
 Рис. 2:
Рис. 2: 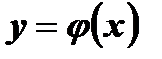
 (Рис. 1) и
(Рис. 1) и 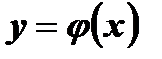 (Рис. 2) определены на
(Рис. 2) определены на 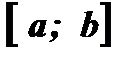 и имеют множество значений
и имеют множество значений 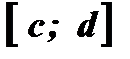 .
. принимает каждое свое значение один раз, то есть у = f ( х ) - обратимая функция.
принимает каждое свое значение один раз, то есть у = f ( х ) - обратимая функция. 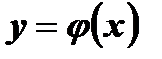 принимает некоторые свои значения не один раз, то есть у = j ( х ) - необратимая функция.
принимает некоторые свои значения не один раз, то есть у = j ( х ) - необратимая функция.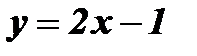 . Построить графики взаимно обратных функций.
. Построить графики взаимно обратных функций.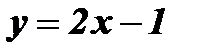 выразим х через у:
выразим х через у: 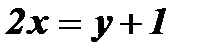 ;
; 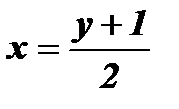 ;
; 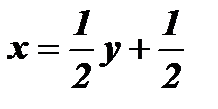 .
.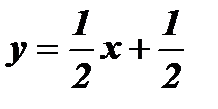 .
.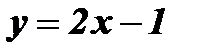 и
и 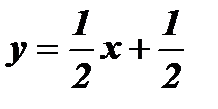 - взаимно обратные функции.
- взаимно обратные функции.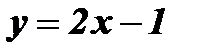 и
и 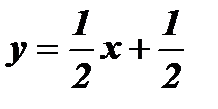 :
:
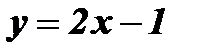 х - 2 2
х - 2 2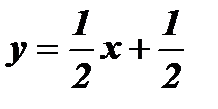
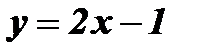 - прямая l1 проходит через точки (- 2; - 5) и (2;3).
- прямая l1 проходит через точки (- 2; - 5) и (2;3). 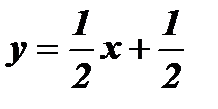 - прямая l2 проходит через точки (- 5; - 2) и (3;2).
- прямая l2 проходит через точки (- 5; - 2) и (3;2). 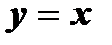 является осью симметрии прямых l1 и l2 .
является осью симметрии прямых l1 и l2 . , надо из формулы
, надо из формулы  выразить х через у и в полученной формуле поменять местами х и у.
выразить х через у и в полученной формуле поменять местами х и у.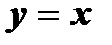 .
.