Настоящая задача посвящается выбору модулей для непосредственного цифрового управления непрерывным технологическим процессом в соответствии со структурной схемой (рисунок 4). Модули ввода-вывода и вычислитель в дальнейшем будем называть цифровым управляющим устройством (ЦУУ). При выполнении контрольной работы необходимо:
4.1.1 В одноканальной системе управления выбрать датчик для измерения указанной в таблице А.2 регулируемой переменной y(t). Выбор датчика осуществлять по заданным в таблице значениям коэффициента χ, величине допустимой погрешности регулирования Δ утз и диапазону изменения регулируемой переменной Dу, взятым из Приложения А. Номер варианта определяется последней цифрой шифра зачетной книжки.
4.1.2 Выбрать ЦУУ для целей управления непрерывным технологическим процессом. В качестве критерия выбора принять минимально возможную длину разрядной сетки.
Так как в качестве критерия выбора модулей ЦУУ задан минимум длины разрядной сетки, то расчеты необходимо начинать с оценки точности вычисления управляющего воздействия.
|
|
Рисунок 4 – Структура системы цифрового управления
Расчет управляющего воздействия u(t) в цифровом вычислителе приводит к появлению ошибки σu, величина которой не должна превышать допустимой σuдоп , т.е.
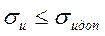(4.1)
Допустимая погрешность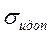 
расчета управляющего воздействия u(t) определяется допустимой ошибкой 
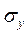регулируемой величины y(t), определяемой техническим заданием (ТЗ). Если объект с самовыравниванием, 
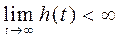, то
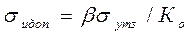(4.2)
где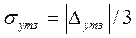 
- среднеквадратическое значение заданной точности регулирования, β - коэффициент, определяющий долю заданной погрешности, отводимую на вычисления (согласно критерию пренебрежимых погрешностей β < 0,3), Ко - коэффициент передачи между выходом ЦАП и выходом объекта управления. Следовательно, он должен учитывать коэффициенты передач исполнительного устройства и объекта (его значение задано в таблице А.2). Размерность Ко определяется как отношение размерности выходной величины объекта к напряжению на выходе ЦАП в Вольтах.
Величина ошибки σu в силу ее случайного характера оценивается как среднеквадратическая, имеющая три составляющие, т.е.
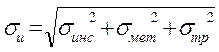, (4.3)
где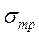 
- среднеквадратическое значение трансформированной ошибки, обусловленной трансформацией погрешностей входных переменных в соответствии с заданным законом управления; 
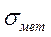- среднеквадратическое значение методической ошибки, возникающей из-за неточной реализации в вычислителе операций интегрирования и дифференцирования; 
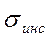- среднеквадратическое значение инструментальной ошибки, обусловленной квантованием по уровню, т.е. конечной длиной разрядной сетки вычислителя.
В общем случае алгоритм управления по отклонениям представляет собой функционал вида
u к =F(u к -i , e к -i+1 ) , i = 1 , 2 , …ν, (4.4)
где F(...) - некоторая функция своих аргументов; u к- i (i=l, 2, ... ν) -предыдущие значения управления; e к- i +1 - значения ошибки рассогласования e(t)=yзад - y(t) при t=(k+1-i)*Tо; То - интервал квантования по времени. Величина v определяется порядком формул численного интегрирования и численного дифференцирования. Например, при использовании формулы численного интегрирования нулевого порядка (формулы прямоугольников) функционал (4.4) для интегрального (И) закона управления будет иметь вид:
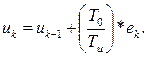(4.5)
С использованием формулы трапеций (интегрирования 1-го порядка) расчет управляющего сигнала в вычислителе выполняется по выражению:
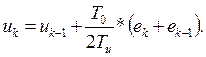(4.6)
При наличии в законе управления дифференциальной составляющей расчет 1-й производной в численном виде выполняется с помощью ряда:
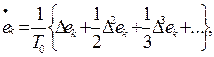(4.7а)
второй производной - в соответствии с уравнением:
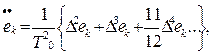(4.7б)
, 
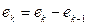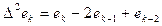, и т.д., причем от количества членов ряда зависит величина методической погрешности определения производной. В системах управления с медленно изменяющимися переменными достаточно брать 2 первых слагаемых ряда (4.7а) и 1 первое слагаемое ряда (4.7б).
Среди линейных законов регулирования в ТАУ наиболее широко используются ПИ-, ПД- и ПИД-законы, которые можно представить в разностной форме:
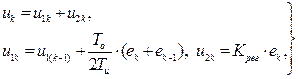(4.8)
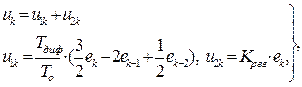(4.9)
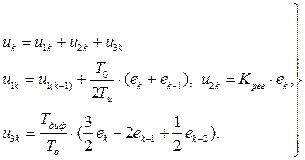(4.10)
В выражениях (4.8) - (4.10):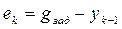 
- сигнал рассогласования, для операции интегрирования использована формула трапеций, для реализации еk взяты два первых слагаемых ряда (4.7а).
Оценку составляющих ошибки σu при расчете управляющего воздействия необходимо производить для установившегося режима работы системы, учитывая следующие соображения: ошибки вычисления σu не накапливаются от шага к шагу, если замыкание главной отрицательной обратной связи происходит на каждом шаге вычислений, все ординаты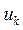 
определяются по одному и тому же алгоритму в одинаковых условиях, поэтому можно считать, что ошибка вычисления Uk не зависит от ошибок предыдущих ординат uk-i (i=1, 2..., v). Следовательно, из формулы (4.4) получаем
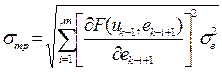, i=1, 2..., v, (4.11)
где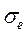 
- среднеквадратическая ошибка сигнала рассогласования, равная среднеквадратической ошибке 
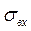на входе вычислителя в предположении, что погрешность g3АД равна нулю, т.е.
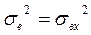(4.12)
Из технического задания на разработку системы обычно известны диапазон изменения Dy и точность регулирования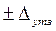 
переменной y ( t ). Для выбора датчика и АЦП необходимо задать χ=0-0,6 - долю общей погрешности, приходящейся на датчик, и ρ=0-0,5 - долю общей погрешности, приходящейся на АЦП так, чтобы произведение 
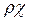располагалось в диапазоне:
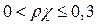(4.13)
При этом остальная величина допустимой погрешности приходится на ошибки вычисления управляющего воздействия и аппаратную погрешность, которая определяется классом точности используемой аппаратуры.
Из выражения (4.13) следует, что, задаваясь значениями коэффициентов ρ и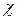 
, можно выбрать датчик и определить разрядность АЦП. В частности, чем меньше будет 
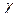, тем точнее будет датчик, а чем меньше будет ρ, тем с большей разрядной сеткой потребуется АЦП. К примеру, задавая 
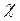= 0,6, т.е. выбирая недорогой грубый датчик, из выражения (4.13) при 
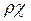= 0,12 получим ρ = 0,2. Следовательно, чтобы обеспечить высокую точность при плохом датчике, необходимо увеличивать разрядную сетку АЦП и вычислителя. Улучшения точности в этом случае добиваются применением программ сглаживания, позволяющих ослабить низкочастотный шум в 
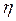=2-10 раз.
При этом среднеквадратическая ошибка сигнала рассогласования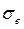 
будет уменьшаться, поскольку 
( 
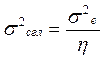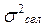- средний квадрат ошибки после сглаживания).
После того как датчик выбран в соответствии с условием
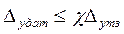(4.14)
с учетом заданного в таблице А.2 значения коэффициента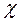 
, из его паспортных данных становятся известны диапазон измерения Dyдam и точность 
.
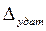В результате дисперсия погрешности на входе вычислителя составит:
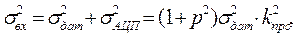(4.15)
где p - коэффициент, величина которого задается в таблице А.2,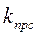 
-коэффициент пересчета изменения реальной физической величины в напряжение на входе АЦП (на выходе датчика 
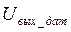). Числовое значение этого коэффициента зависит от максимального значения физической величины умакс, измеряемой датчиком, и от максимального входного напряжения АЦП (часто это 10 В), т.е.
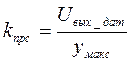. (4.16)
на основании формул (4.8)-(4.16) можно рассчитать величину трансформированной погрешности.
Например, при П-законе управления производная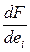 
= kрег , следовательно, дисперсия трансформированной погрешности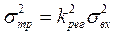 
или с учетом (4.15)
.
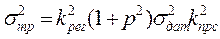При ПИД-законе в случае интегрирования по трапециям и использования для вычисления производной 2-х членов ряда (4.7а)
.
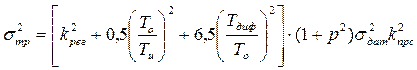Среднеквадратическое значение методической погрешности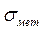 
при её нормальном распределении определяется выражением
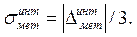(4.17)
Абсолютная величина методической погрешности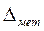 
при интегрировании по методу прямоугольников:
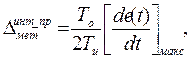
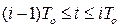, (4.18)
а при интегрировании по методу трапеций:
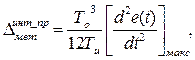
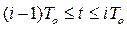. (4.19)
Таким образом, зная максимальные значения 1-й и 2-й производных ошибки рассогласования и величину интервала дискретности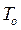 
, можно, пользуясь формулами (4.17), (4.18) или (4.17), (4.19), вычислить дисперсию методической погрешности 
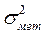на шаге 
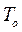при вычислении интеграла.
Абсолютное значение методической погрешности получения первой производной, вычисляемой по (4.7а) с 2-мя членами ряда будет равно:
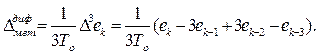(4.20)
В то время как использование одного слагаемого в (4.7а) приводит к методической погрешности дифференцирования следующего вида:
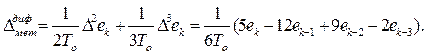(4.21)
Для оценки инструментальной погрешности, обусловленной ограниченной длиной разрядной сетки вычислителя, необходимо знать эту длину. Из практики и литературы известно, что АЛУ вычислителя должно превышать разрядность АЦП на величину d, т.е.
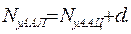(4.22)
При этом величина младшего разряда АЛУ вычислителя составит
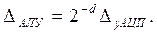(4.23)
Величина d не должна быть меньше 4-х, чтобы результат не был искажен вычислительными погрешностями, и окончательная длина разрядной сетки АЛУ должна быть кратна байту.
Длина разрядной сетки АЦП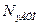 
рассчитывается в соответствии с выражением:
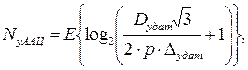(4.24)
в котором операция Е{...} означает округление результата до ближайшего целого в большую сторону, а коэффициент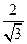 
появляется из-за разницы в вычислении дисперсий погрешностей датчика и АЦП. Так как погрешность датчика подчиняется нормальному закону распределения, а погрешность АЦП - равномерному, то дисперсии соответствующих погрешностей будут равны:
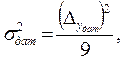
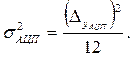
Следовательно, учитывая, что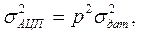 
величину младшего разряда АЦП можно определить как
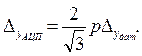(4.25)
Для окончательной оценки инструментальной погрешности необходимо подсчитать количество округлений m в формуле вычислений управляющего воздействия и определить дисперсию единичного округления в АЛУ с учетом равномерного закона распределения как
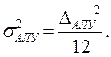
В результате полная инструментальная погрешность вычисления на шаге То управляющего воздействия
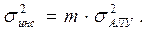(4.26)
После того как все составляющие погрешности вычисления управляющего воздействия определены, следует проверить условие (1). Если оно не выполняется, то нужно определить, какую из погрешностей необходимо уменьшать в первую очередь.
Уменьшить погрешность метода можно, во-первых, путем уменьшения интервала дискретности То, во-вторых, использованием более точных формул численного интегрирования и дифференцирования, пересчитав при этом значение инструментальной погрешности и опять проверив условие (4.1).
Уменьшение значения То ограничивается, прежде всего, возможностями используемых технических средств, поскольку за это время должны быть выполнены следующие процедуры: опрос датчиков, преобразование аналоговых отсчетов в код, первичная обработка, вычисление кода управляющего воздействия, преобразование его в напряжение и передача сигнала управления в исполнительное устройство.
Уменьшение величины трансформированной погрешности в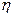 
(2 < 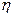< 10) раз можно добиться введением алгоритмов сглаживания.
Величина инструментальной погрешности уменьшается только использованием устройств с большей длиной разрядной сетки.
Выбор ЦАП осуществляется по требуемому количеству разрядов, которое рассчитывается по формуле:
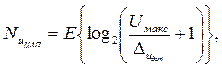(4.27)
где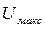 
- величина максимального напряжения на выходе ЦАП (например, 5 В), 
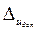- цена младшего разряда ЦАП, которая с учетом равномерного распределения инструментальной погрешности и формулы (4.1) имеет следующий вид:
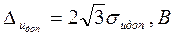(4.28)
После выполнения и изложенных выше расчетов необходимо из каталогов фирм-производителей, например [6], подобрать соответствующие модули, отвечающие требованиям по точности преобразований и вычислений, привести их марку и технические характеристики.
4.2 Выбор комплекса технических средств (пример)
Выбрать модули ЦCУ, предназначенного для поддержания уровня h раствора в баке. Диапазон изменения уровня раствора: D у = 6,0 – 7,5м, точность поддержания: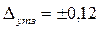 
м. Указанный диапазон обеспечивается перестановкой регулирующего органа на 25%, следовательно, коэффициент передачи объекта управления
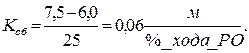
Коэффициент передачи К о между выходом ЦАП и выходом ОУ составляет 0.7 м/В. Остальные данные сведены в таблицу4.1, аналогичную таблице А.1.
Таблица 4.1 – Исходные данные для расчета ЦСУ для поддержания уровня
| Закон регулиро-вания
| Ко, м/В
| Крег
| Ти, с
| Tдиф,с
| χ
| Р
| Т о,с
| Значения сигнала рассогласования | |||
| ек, В | ек-1, В | ек-2, В | ек-3, В | ||||||||
| ПИ | 0,7 | 9,5 | 4,04 | - | 0,2 | 0,3 | 1 | 0,97 | 0,92 | 0,8 | 0,55 |
Реализация задачи будет состоять из следующих шагов:
1. В соответствии с выражением (4.2) рассчитаем допустимое значение погрешности вычисления управляющего воздействия, полагая Р=0,3
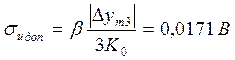
2. По требуемой точности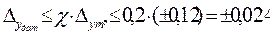 
м и заданному диапазону изменения уровня выбираем датчик УДУ-5П с диапазоном измерения уровня D у = 0-12 м и погрешностью показаний 
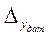= ±0,015 м.
3. По формуле (4.24) рассчитываем разрядность АЦП
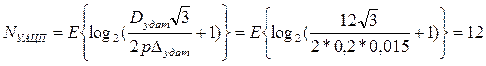
4. Определяем разрядность ЦАП (4.27):
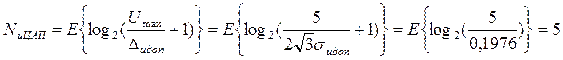
5. Определяем погрешность вычисления управляющего воздействия.
5.1. Расчет начнем с трансформированной погрешности, пользуясь формулами (4.4), (4.5), (4.8), (4.12), (4.15) и (4.16). В качестве формулы численного интегрирования в выражении (4.8) вместо формулы трапеций выбрана формула прямоугольников (4.5) как более простая.
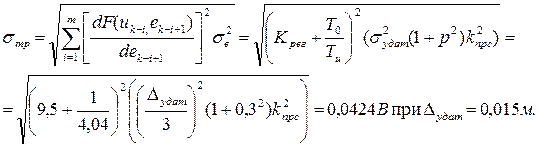
при ∆удат=0,015м.
5.2. По (4.7а), (4.17), (4.18), пользуясь числовыми данными, приведенными в таблице А.3, находим величину методической погрешности:
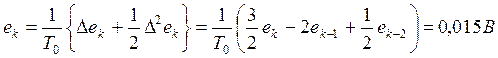
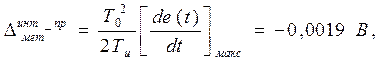
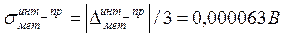
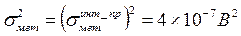
Если в алгоритм управления (4.4) входит дифференциальная составляющая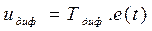 
, где Тдиф – постоянная времени, величина которой задается в исходных данных, то методическая погрешность численного дифференцирования вычисляется по (4.20) или (4.21), а дисперсия методической погрешности для ПД-закона составит:
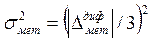
В то время как для ПИД-закона управления она имеет вид:
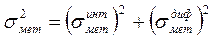
5.3. Для оценки инструментальной погрешности по (4.26) выбираем разрядность АЛУ (4.22) с учетом (4.23) и (4.24), оцениваем величину младшего разряда процессора (4.25) и количество округлений m в формулах вычисления управляющего воздействия.
Задавшись коэффициентом d, равным 4, получаем 16-и разрядную сетку АЛУ и величину
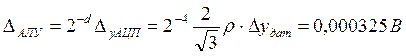
Количество округлений m можно найти, если записать алгоритм расчета в АЛУ управляющего воздействия по ПИ-закону с использованием выбранной формулы численных вычислений (черточками обозначена процедура округления):
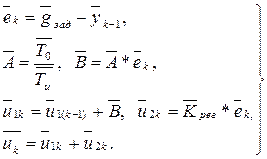
В представленной системе уравнений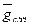 
- требуемое значение регулируемой переменной у. Как видно из этой системы, количество округлений m равно 12 (следует заметить, что при определении m нельзя дважды учитывать округление одной и той же величины, например, 
, 
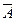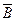или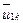 
, 
).
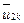Так как инструментальная погрешность в пределах младшего разряда АЛУ подчиняется равномерному закону распределения, то, как было сказано выше, дисперсия единичного округления микроконтроллера
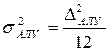
и следовательно, инструментальная погрешность АЛУ при вычислении управляющего воздействия для рассматриваемого примера составит следующую величину:
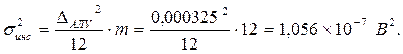
Проверяем условие (4.1). С этой целью по выражению (4.3) определим значение суммарной погрешности вычисления как
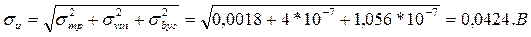
Сравнивая полученное значение с допустимым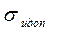 
= 0,0171, убеждаемся, что условие (4.1) не выполняется из-за большой по величине трансформированной погрешности. Как отмечалось ранее, для её уменьшения необходимо ввести алгоритм экспоненциального сглаживания с коэффициентом ослабления
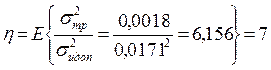
после чего условие (4.1) будет выполнено
6. Из каталога фирмы ProSoft [6] в соответствии с выполненными расчетами находим модули ввода-вывода и контроллер, отвечающие требованиям по точности преобразований и вычислений и имеющие разрядные сетки по длине не хуже рассчитанных. Из модулей фирмы ADVANTECH можно использовать следующие:
а) модуль аналогового ввода ADAM-4012 с параметрами: 16-разрядный АЦП, Программная настройка для работы с мВ, В или мА, гальваническая изоляция 500 В, 1 цифровой вход/счетчик событий, 2 цифровых выхода/аварии по верхней и нижней границам измеряемого входа;
б) модуль аналогового вывода ADAM-4021 с параметрами: 12-разрядный ЦАП, программная настройка выхода на В или мА, контроль состояния выхода, программируемая скорость изменения сигнала на выходе: от 0,125 до 128,0 мА/с или от 0,0625 до 64 В/с, гальваническая изоляция 500 В;
в) ADAM-5511 - IBM PC-совместимый программируемый микроконтроллер. Микроконтроллер ADAM-5511 представляет собой аналог ADAM-5510, в котором реализована программная поддержка популярного протокола ModBus, что позволяет обмениваться данными с любым программным обеспечением верхнего уровня (SCADA) без использования специальных драйверов. Кроме того, ADAM5511 обеспечивает возможность удаленной загрузки, запуска, останова и завершения программ. IBM PC совместимый программируемый микроконтроллер ADAM-5510: процессор: 80188, 16-разрядный, память ОЗУ: 256 кбайт, флэш-ПЗУ: 256 кбайт, операционная система: ROM-DOS, часы реального времени встроенные, сторожевой таймер встроенный, количество обслуживаемых модулей ввода-вывода: до 4, 2 последовательных порта: RS-232 и RS-485, напряжение изоляции 3000 В.
Окончательный выбор зависит от стоимости блоков
Заключение
Знания и умения, полученные студентом при выполнении курсового проекта, будут использованы во время дипломного проектирования, когда потребуется составление раздела, рассматривающего вопросы метрологического обеспечения автоматизации производства.
Контрольные вопросы
1. Какие факторы учитывают при нахождении композиции законов распределения погрешностей ?
2. Как наличие корреляции погрешностей влияет на способ их суммированя?
3. В чем принципиальное отличие иннформационно-энтропийного подхода к суммированию погрешностей от вероятностного?
4. Для какой доверительной вероятности допускается упрощенное суммирование составляющих погрешности?
5. Что используется в качестве критерия выбора цифровых управляющих устройств?
6. Что определяет инструментальную погрешность вычислителя?
7. Сформулируйте условие согласованности погрешностей датчика и АЦП?
Библиографический список
1. СТП 3.4.204-01. Система вузовской учебной документации. Требования к оформлению текстовых документов. - Красноярск: СибГТУ, 2001.- 48 с.
2. СТП 3.4.104-01. Курсовое проектирование [Текст] Требования к выполнению и форме представления. - Красноярск: СибГТУ, 2002.- 12 с.
3. Сергеев, А.Г. Метрология: Учебное пособие для вузов [Текст] /А.Г. Сергеев, В.В. Крохин.- М.: Логос, 2000. - 408с.
4. Пьявченко, Т.А. Программа, методические указания и контрольные
работы по дисциплине “Технические средства автоматизации и
управления” [Текст] / Т.А.Пьявченко -Таганрог: 2005. - 58с.
5. Слепова, С.В. Основы теории точности измерительных приборов: Учебное пособие [Текст] / С.В. Слепова. – Челябинск: Изд-во ЮУрГУ, 2008. – 192 с.
6. Каталог продукции ПРОСОФТ ©2010 ProSoft http://www.prosoft.ru,
http://asutp.prosoft.ru/products/brands/advantech/
Содержание
Введение…………………………………………………………………3
1 Задание на курсовую работу………………………………………......4
1.1 Исходные данные…………………………………………………….4
1.2 Задачи курсовой работы……………………………………………..5
2 Состав и основные требования к курсовой работе…………………..6
3 Методические указания к расчету погрешности
измерительного канала………………………………………………8
3.1 Основные теоретические сведения о суммировании погрешностей…………………………………………………………8
3.2 Пример расчета погрешности типового измерительного канала...16
3.3 Сравнение приближенных методов суммирования……………....28
4 Обоснование выбора модулей ЦСУ методом
согласованных погрешностей.……………………………………….31
4.1 Алгоритм расчета погрешностей и его основные допущения……31
4.2 Выбор комплекса технических средств …………………………...43
Заключение……………………………………………………………..48
Контрольные вопросы…………………………………………………..49
Библиографический список ………………………………………….50
Приложения…………………………………………………………….52
Приложение А (обязательное)………………………………………….52
Приложение Б (обязательное)………………………………………….55
Приложение В (справочное)……………………………………………57
Приложение А (обязательное)
Таблица А.1 – Исходные данные для расчета погрешности ИК
| Последняя цифра номера зачетки | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Rд, Ом | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 100 |
| R ,Ом | 100 | 100 | 100 | 200 | 250 | 300 | 350 | 350 | 400 | 400 |
| γ mg , % | 0,15 | 0,05 | 0,1 | 0,025 | 0,02 | 0,01 | 0,05 | 0,1 | 0,15 | 0,05 |
| п, витков | 500 | 1000 | 200 | 300 | 2000 | 700 | 120 | 250 | 800 | 1500 |
| Eд, мВ | 200 | 350 | 300 | 170 | 500 | 800 | 700 | 100 | 600 | 190 |
| Кст | 15 | 25 | 20 | 15 | 25 | 20 | 15 | 25 | 20 | 15 |
| Ку | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
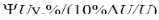
| 0,03 | 0,01 | 0,05 | 0,03 | 0,01 | 0,05 | 0,03 | 0,02 | 0,05 | 0,03 |
| ψθу, %/10°С | +0,2 | |||||||||
| Класс точности ЦВ, c/ d | 02/01 | 01/05 | 05/02 | 01/05 | 02/01 | 01/05 | 02/01 | 05/02 | 01/05 | 05/02 |
| rсв, Ом | 1,5 | 2,0 | 2,5 | 1,5 | 2,0 | 1,5 | 2,5 | 2,0 | 1,5 | 2,5 |
| U нав,, мВ | 3600 | 1600 | 900 | 500 | 1800 | 2400 | 800 | 500 | 950 | 200 |
| θлаб, °С | 21±3 | |||||||||
| Θцех, °С | 20±10 | |||||||||
| Доверительная вероятность, Рд | 0,99 | 0,95 | 0,98 | 0,85 | 0,98 | 0,95 | 0,95 | 0,98 | 0,95 | 0,99 |
| Класс точности АР | 0,025 | 0,02 | 0,01 | 0,025 | 0,02 | 0,01 | 0,02 | 0,025 | 0,01 | 0,02 |
Таблица А.2 – Исходные данные для расчета погрешности ЦСУ
| В а р | ОУ и канал регулирования | Закон регули рования | Ко | Крег | ТИ ,с | Тдиф, с |
| Р | То, с | Значения сигнала рассогласования | |||
| 
| 
| 
| ||||||||||
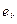
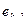
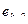
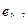
| 0 | Парогенератор: Расход топлива – давление перегретого пара | ПИД | 0,15 | 30 | 250 | 24 | 0,5 | 0,5 | 8 | 0,47 | 0,62 | 0,78 | 0,92 |
| 1 | Парогенератор: Расход воды на впрыск – температура перегретого пара | ПИД | 1,46 | 0,4 | 80 | 24 | 0,5 | 0,2 | 2 | 0,16 | 0,374 | 0,6 | 0,836 |
| 2 | Теплица: Расход воды на обогрев – температура воздуха | ПИ | 20 | 3 | 600 | - | 0,6 | 0,5 | 10 | 0,2 | 0,4 | 0,65 | 0,85 |
| 3 | Теплица: Расход воды на распыление – влажность воздуха | ПИ | 60 | 0,5 | 600 | - | 0,4 | 0,4 | 5 | 0,4 | 0,55 | 0,75 | 0,9 |
| 4 | Турбина: Положение регулирующего клапана - частота вращения | ПИД | 105 | 0,43 | 353,5 | 501 | 0,2 | 0,5 | 0,6 | 0,18 | 0,38 | 0,6 | 0,82 |
| 5 | Смеситель 1: Расход потока F1 – концентрация выходного потока С0 | ПИ | 1,25 | 1 | 50 | - | 0,6 | 0,1 | 5 | 0,15 | 0,3 | 0,6 | 0,9 |
| 6 | Смеситель 2: Расход холодной воды – температура смеси | ПИ | 4 | 4 | 250 | - | 0,3 | 0,5 | 2,5 | 0,2 | 0,4 | 0,65 | 0,9 |
| 7 | Генератор переменного тока: Напряжение на выходе – ток возбуждения | ПД | 10 | 1 | - | 0,3 | 0,3 | 0,4 | 0,05 | 0,5 | 0,55 | 0,75 | 0,94 |
| 8 | Сушка: Температура на выходе топки – расход топлива | ПИ | 20 | 0,014 | 800 | - | 0,6 | 0,15 | 100 | 0,4 | 0,6 | 0,75 | 0,9 |
| 9 | Сушка: Влажность сухого жома – расход топлива | ПИД | 40 | 400 | 1 | 20 | 0,6 | 0,25 | 20 | 0,35 | 0,55 | 0,7 | 0,8 |
Таблица А.3 - Значение коэффициентов для пяти видов распределений
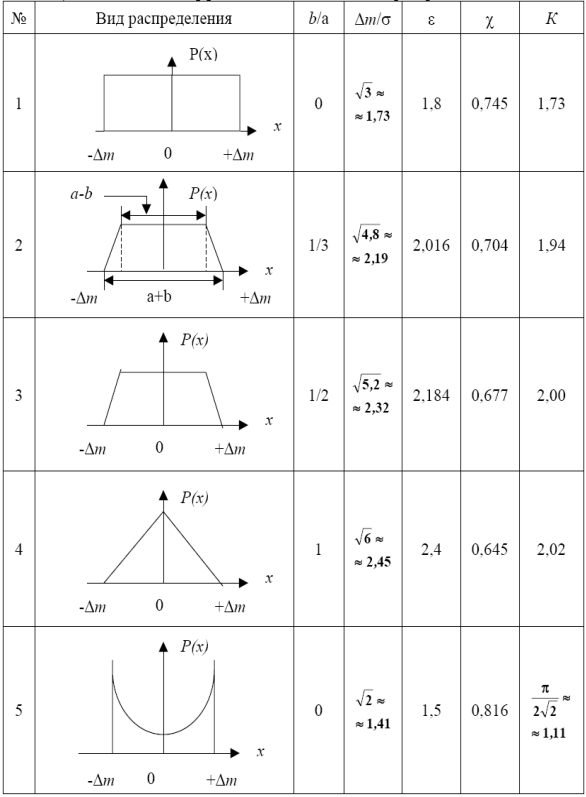
Приложение Б (обязательное)
Образец бланка задания на проектирование
Федеральное агентство по образованию РФ
Дата: 2018-12-21, просмотров: 615.
