Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Основные теоретические представления о

Суммировании погрешностей

 

Результирующую погрешность информационно-измерительного канала можно найти как композицию законов распределения погрешностей отдельных узлов, составляющих этот канал. При нахождении композиции надо учитывать 3 фактора:

1) числовые характеристики законов распределения составляющих могут меняться в диапазоне измерения;

2) отдельные слагаемые суммы могут быть коррелированы ;

3) при суммировании случайных величин происходит изменение формы  законов распределения.

Для учета первого фактора погрешности составляющих делят на аддитивные и мультипликативные и суммирование их ведут раздельно. Второй фактор учитывают введением коэффициентов корреляции в формулы результирующей дисперсии. Третье обстоятельство учитывают с помощью параметров формы – контрэксцесса χ и энтропийного коэффициента k . Величиной контрэксцесса χ удобно пользоваться для классификации распределений по их форме, изменяющейся для любых законов распределения в пределах от 0 до 1:

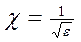                                                                                                     (3.1)

где ε - эксцесс - может для различных законов распределения иметь значение от 1 до ∞.

Для оценки величины разброса случайных погрешностей относительно центра, т.е. ширины распределения, на практике используется ряд различных приемов. Предельная (максимальная) оценка случайной погрешности правомерна только для ограниченных распределений (равномерного, трапецеидального, треугольного, арксинусоидального и т.п.). Для этих распределений теоретически существует такое значение ± χ_т , которое ограничивает с обеих сторон возможные значения случайной величины. Кривые плотности реальных распределений обычно не имеют четко выраженных границ. И поэтому неправомерно указание для них предельных значений, а тем более арифметическое суммирования предельных значений (получаемая сумма может в разы превышать реальные погрешности).

Оценка разброса случайных величин возможна средним квадратическим отклонением (СКО) σ, достоинством которой является возможность определения дисперсии суммы статистически независимых величин  безотносительно к видам законов распределения каждой из суммируемых величин и деформации законов распределения при образовании композиций.

Таким образом, для того чтобы отдельные составляющие погрешности СИ можно было суммировать, они должны быть предварительно представлены своими средними квадратическими значениями σ .

При практическом использовании информационного подхода для оценки точности результатов измерений рационально оперировать понятием энтропийного значения погрешности ∆_э = k 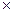σ , а энтропийный коэффициент k определяет ее связь с СКО для различных законов распределения.

В таблице А.3 приведены значения ε, χ, k,  а также Δ m /σ для ограниченных распределений (равномерного, арксинусоидального, трапецеидального и треугольного).

В общем случае СКО суммы равно    

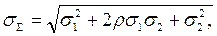
                                     (3.2)

                                                                                                 

где ρσ₁ σ ₂ - взаимный корреляционный момент.

Если σ₁ и σ₂ между собой не коррелированы, то ρ = 0 и

 

σ_Σ = 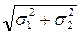,                                                                        (3.3)

 

т. е. СКО составляющих суммируются геометрически.

Если случайные величины жестко и положительно коррелированы между собой (ρ = + 1 ) , то всякое поло­жительное отклонение одной величины сопровождается также положительным отклонением второй, тогда

 

σ_Σ = σ₁ + σ₂,                                                                            (3.4)

 

Если при возрастании одной величины вторая линейно убывает, то ρ = -1 и σ_Σ = σ₁ - σ₂. Таким образом, оценки жестко коррелированных погрешностей (ρ=±l) должны суммироваться не геометрически, а алгебраически с учетом их знаков. При решении вопросов расчетного суммирования погрешностей обычно интересуются разграничением сильной (ρ > 0,7) и слабой (ρ ≤ 0,7) корреляционной связи суммируемых погрешностей.

Практические правила расчетного суммирования составляющих результирующей погрешности следующие:

1)  должны быть учтены взаимные корреляционные связи различных
составляющих погрешности (часто различных узлов канала);

2) для каждой составляющей должно быть найдено СКО. В большинстве случаев для этого необходимо знание или предположение о виде закона распределения каждой из составляющих;

3) все составляющие подразделяются на аддитивные и мультипликативные и суммируются раздельно;

4) из суммируемых составляющих выделяются группы сильно
коррелированных между собой составляющих погрешности и внутри этих
групп производится алгебраическое суммирование их оценок;

5) После того, как все группы сильно коррелированных погрешностей выделены и внутри их произведено алгебраическое суммирование, суммарные по группам и оставшиеся вне групп погрешности можно считать уже некоррелированными и складывать их геометрически. Для определения СКО при х=0 складываются лишь аддитивные составляющие, а для определения СКО погрешности в конце диапазона измерений - все суммируемые составляющие;

6 ) для перехода от СКО погрешности к энтропийному Δ_э = k_Σ σ_Σ или доверительному Δ_д = t_Σ σ _Σ значениям должно быть вынесено суждение о форме закона распределения результирующей погрешности и, значит, выбрано значение энтропийного коэффициента k_Σ или квантильного множителя t_Σ;

7) при определении энтропийного значения погрешности для него также может быть указано соответствующее значение доверительной вероятности

P_э = 0,899 + χ² /5,5                                                                  (3.5)

При этом значении доверительной вероятности энтропийное и доверительное значения погрешности совпадают. Для перехода к интервальной оценке в виде доверительного Δ_д = t_Σ · σ _Σ или энтропийного Δ_э = k_Σ ·σ_Σ значений необходимо знание лишь его одного числового параметра в виде квантильного множителя t_Σ или энтропийного коэффициента k_Σ, причем определение энтропийного значения результирующей погрешности является наиболее точным методом расчетного суммирования погрешностей.

Сводка зависимостей энтропийного коэффициента k_Σ от соотношения суммируемых составляющих и их энтропийных коэффициентов может быть представлена в виде семейства графиков (рисунок 2), где по оси абсцисс отложены значения относительного веса дисперсии 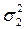 второго из суммируемых распределений в полной дисперсии  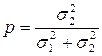по оси ординат – значение энтропийного коэффициента k_Σ образующейся при этом композиции.

Несмотря на то, что кривые рисунке 2 построены только для нескольких видов законов распределения, их сетка настолько густа, что позволяет визуально интерполировать значения k_Σ для любых законов распределения с известным энтропийным коэффициентом.

При расчете результирующей погрешности с произвольным значением заданной доверительной вероятности необходимо пользоваться соотношением для вычисления эксцесса распределения суммы двух независимых случайных величин по их эксцессам ε(х) и ε(у) :

 

 ε_Σ=ε(x)p²+6p(1-p)+ε(y)(1-p²),                                                        (3.6)

 

где вес дисперсии первого распределения в общей дисперсии находится по формуле

 p = σ²_x/(σ²_x+σ² _y )                                                                    (3.7)

Следовательно, для расчета результирующей погрешности этим методом для каждого из суммируемых составляющих надо знать оценки ε ( x ), σ_x и ε(у), σ _y . Затем находится σ_Σ = 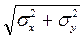, по (1-7) определяется вес дисперсии одной из составляющих, а по (1-6) находится оценка ε_Σ  суммарной погрешности. Если суммируемых составляющих больше двух, то суммирование и определение ε_Σ  производится последовательно - первой со второй, затем полученной с третьей и так далее.

В курсовой работе рассчитывают метрологические характеристики типового измерительного канала и проводят их грубое нормирование. Поскольку при расчете требуется принять целый ряд эвристических решений с привлечением дополнительных исходный сведений, то с целью сокращения объема методических указаний они даны в виде конкретного примера расчета типового измерительного канала. Типовой канал состоит из серийно выпускаемых узлов (реостатного датчика Д, линии связи ЛС, усилителя У, аналогового регистратора (АР), цифрового вольтметра (ЦВ), блока питания БП, стабилизатора напряжения (СН) и имеет следующие исходные данные:

-  сопротивление датчика Rд, Ом	.…………………………….200
- класс точности датчика γmg , %	…………………………….0,15
- число витков обмотки датчика п	.…………………………….500
- напряжение питания датчика Е g , мВ	.…………………………….200
- коэффициент стабилизации СН Кст	.……………………………...25
- коэффициент усиления У, Ку	………………………………..1
- коэффициент влияния колебаний напряжения питания усилителя на коэффициент усиления Ку , ψUy ,% (10% ∆ U / U )	.………………………….…+0,3
- коэффициент влияния температуры  на коэффициент усиления ψθу, %/10°С	.…………………………..…+0,2
- напряжение сети Е , В	……………………………...220
- нестабильность напряжения сети σс , %	……………………………...+15
- сопротивление проводки линии связи датчика с усилителем rСВ, Ом	.……………………………….2
- напряжение наводки частотой 50 Гц , измеренное с помощью электронного вольтметра с входным сопротивлением 1 МОм , U НАВ , мВ	……………………….……1600
- пределы изменения температуры в лаборатории Θлаб , °С	………………………….…21+3
- закон распределения температуры в цехе нормальный с доверительной вероятностью Р д	..……………………………0,98
- изменения температуры в цехе, где установлен датчик Θ , °С	...…………………………20±15
- класс точности АР, q	...…………………………….0,5
- температурное смещение нуля ψΘрег = −0,1% /10 K	…………………..…………...0,2
- класс точности ЦВ , c / d	……..……………………0,2/0,1
- количество знаков отсчета ЦВ	………………..……………….3

 

 

 

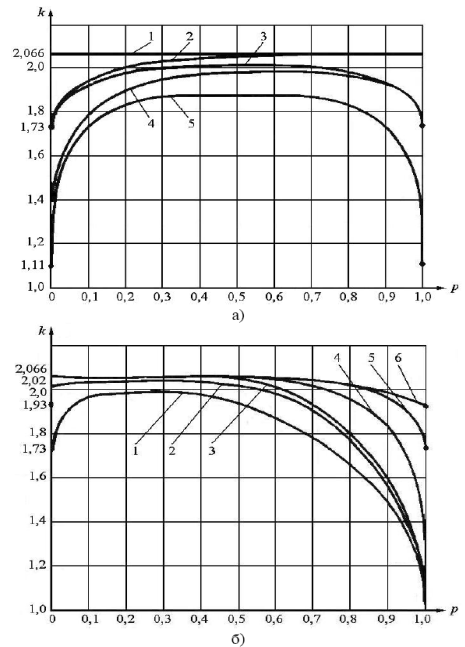
Рисунок 2 – Сводка зависимостей энтропийного коэффициента k_Σ 

от соотношения суммируемых составляющих p:

а) композиция двух распределений

1 - для композиции двух нормальных распределений;

2- для равномерно распределенной погрешности (к_Σ1 = 1,73) с нормально распределенной (к_Σ2 = 2,066);

3 - для двух равномерных распределений ;

4 - для арксинусоидального и равномерного распределений;

б) композиция трех распределений

1,2,3 - для композиции равномерного, треугольного и нормального распределений с дискретным двузначным распределением;

4,5,6 - для композиции нормального распределения соответственно с арксинусоидальным, равномерным и экспоненциальным.

Пример расчета погрешности измерительного канала

 

При расчете результирующей погрешности ИК необходимо каждой из составляющих погрешности приписать соответствующий закон распределения, найти СКО и подразделить погрешности на аддитивные и мультипликативные. Все расчеты как максимальных погрешностей, так и СКО будем вести в относительных приведенных значениях.

3.2.1 Погрешность от наводки на линию связи может быть приближенно рассчитана следующим образом. При присоединении к линии электронного вольтметра с входным сопротивлением R _ВХ = 1 МОм падение напряжения на этом сопротивлении составляет 1600 мВ, т. е. через него проходит ток

 

 

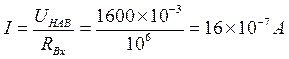
При замыкании линии связи на сопротивление датчика R_д =200 Ом падение напряжения на нем от этого тока составит

 

U = I 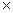R_Д = 16 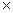10^-7 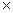200 = 0,32 мВ

 

Таким образом, приведенная погрешность от наводки при максимальном сигнале с датчика, равном 200 мВ, будет

 

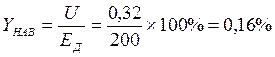
Поскольку исходное значение наводки U _НАВ = 1600мВ было отсчитано по шкале вольтметра как действующее (среднее квадратическое ) значение, то полученная оценка погрешности от наводки и есть её СКО σ_НАВ= 0,16% .

Погрешность от наводки на вход прибора или линии связи синусоидального напряжения силовых цепей с частотой 50 Гц имеет арксинусоидальное распределение. Следовательно (таблица А.3), энтропийный коэффициент этого распределения k _НАВ = 1,11 , контрэксцесс χ = 0,816 , эксцесс ε = 1,5. Максимальное значение погрешности от наводки

 

γ _{MAX НАВ} = σ 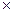 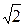= 0,16 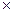1,41 = 0,225%.

В данном случае напряжение наводки возрастает линейно с ростом входного сигнала, т. е. погрешность наводки является мультипликативной.

3.2.2 Определим СКО Датчика, исходя из следующих соображений. Основная по­грешность Датчика нормирована по паспорту максимальным значением у_mД = 0,15%. Для того, чтобы от этого значения перейти к СКО, необходимо знание вида закона распределения погрешности. Одной из составляющих погрешности Датчика является погрешность дискретности, обусловленная конечным числом витков его обмотки, по которым скользит подвижный контакт. Эта погреш­ность имеет равномерное распределение. Абсолютная погрешность дискретности ∆ при п = 500 составляет ± 0,5 вит. Относительная погрешность дискретности

 

 

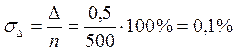
Однако для Датчика погрешность нормируется как 0,15%. Следовательно, есть еще другие, неизвестные составляющие (погрешность нелинейности, т. е. неравномерность намотки, люфт и т.п.). Но так как они незначительно увеличили результирующую погрешность, то преобладающей является погрешность дискретности и поэтому общее распределение погрешности можно считать близким к равномерному. Тогда γ_mД = 0,15% можно считать половиной ширины этого равномерного распределения, а СКО составит σ_Д = γ_mД / 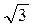= 0,087%. В соответствии с Таблицей А.3 для равномерного распределения k =1,73, χ=0,745 и ε=1,8.

3. 2.3 Определим температурную погрешность Датчика, исходя из следующих соображений. Датчик с R _Д =200 Ом включен последовательно с двумя жилами медной линии сопротивления r _СВ=2 Ом каждая. Абсолютное изменение сопротивления каждой из жил составит

 

,

 

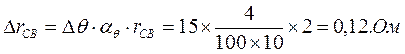где а_θ =+ 4%/10 °С – температурный коэффициент меди.

Относительная температурная погрешность Датчика

 

 

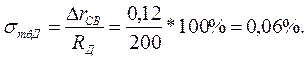
Поскольку закон распределения температуры в испытательном цехе нормальный, то по таблице нормального распределения находим, что вероятности P_д = 0,98 соответствуют границам ±2,3σ. Отсюда СКО

 

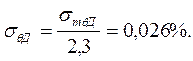
Параметры закона распределения k =2,066; ε =3; χ = 0,577.

3.2.3 Определим зависимость погрешности Датчика от колебаний напряжения питания. Она мультипликативна и распределена по тому же закону, что и отклонения напряжения сети от своего номинального значения 220 В. Распределение напряжения сети близко к треугольному с пределами ± 15%.

Стабилизатор снижает размах колебаний напряжения в Кст =25 раз, т.е. на выходе СН распределение также треугольное, но с размахом 15%/25 = 0,6%. Поэтому максимальное значение этой погрешности γ _mU = 0,6%. Согласно рисунку 2 СКО для треугольного распределения σ_uД = γ _mU / 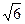= 0,245%. Параметры этого распределения : k = 2,02;  ε = 2,4;  χ = 0,65.

3.2.5 Погрешность коэффициента усиления является мульти­пликативной и распределена также по треугольному закону, так как вызывается колебаниями напряжения питания. Максимальное значение погрешности

 

γ mU Д = 0,03  10-2  15 = 0,45%. СКО составляет σU Д = γ mД/  = 0,184%.

 

Параметры распределения согласно п.3.2.3 k =2,066; ε = 3; γ ⁼⁼ 0,577.

3.2.6 Погрешность смещения нуля усилителя при колебании температуры является аддитивной, а закон ее распределения повторяет закон распределения температуры в лаборатории, где установлены усилитель и ЦВ. Поскольку закон распределения температуры в лаборатории в пределах от 18 до 24 ° С можно считать равномерным со средним значением 21° и размахом ±3° С , то максимальное значение этой погрешности при ψ_θу = 0,2%/10°С составляет γ _mθу =ψ_θу·∆θ = 2х3/10 = 0,06%. СКО σ_{θ y} =0,06/ 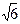 = 0,034%. Параметры этого распределения k =1,73, χ = 0,745 и ε = 1,8.

3.2.7 Погрешность ЦВ нормирована двучленной формулой. Ее приведенное значение равно 0,15 при Х = 0 и линейно возрастает до 0,2% в конце шкалы. Но при использовании в измерительном канале ЦВ возникает ситуация, которая требует особого рассмотрения.

Максимальный сигнал датчика в данном случае равен 200 мВ. При номинальном коэффициенте усиления Усилителя К_e = 1, выходное напряжение Усилителя также равно 200 мВ. Пределы измерений ЦВ, как правило, кратны 10 (например, 100, 10 и 1В). При использовании в рассматриваемом канале измерений на пределе 1000 мВ он обеспечивает удобный отсчет измерений непосредственно в мВ, но расчет его погрешности в этом случае имеет некоторые особенности, ввиду неполного использования шкалы.

Особенность расчета погрешности в таком случае состоит в том, что приведенное значение погрешности должно рассчитываться для предела измерений именно 200 мВ, в то время как приведенная погрешность ЦВ дана для предела измерений Хк = 1000 мВ. Для этого должна быть вычислена абсолютная погрешность в точках начала и конца этого нового диапазона и отнесена к его концу. Абсолютная погрешность при Х = 0 ЦВ класса c / d

∆₀= d 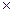X _к /100=0,1 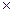1000/100=1мВ

 

Приведенное значение погрешности к пределу измерений Хк  канала

 

γ_НЦВ = ∆₀ 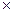100/200 = 0,5%.

 

Абсолютная погрешность ЦВ при Х=200Мв 

 

∆₂₀₀ =∆₀ +[(c - d)/100 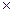200]= 1,2 мВ.

 

Приведенное к пределу измерений канала значение погрешности

 

γ_КЦВ =∆₂₀₀ / X _КАН =1,2 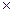100/200 = 0,6%.

 

Таким образом, неполное использование диапазона ЦВ приводит к существенному возрастанию приведенной погрешности измерения, в данном случае с 0,2/0,1 до 0,6/0,5. Для перехода от максимальной погрешности ЦВ к СКО необходимо знание вида закона распределения этой погрешности. Будем считать, что распределение погрешности ЦВ является композицией равномерного распределения и экспоненциального с показателем степени а = 0,5 и с дисперсией, составляющей 1/13 общей дисперсии. Тогда погрешность ЦВ содержит две части при Х = 0:

 

 ; ;

 

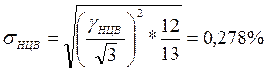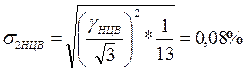 И в конце диапазона измерений канала:

 

; .

 

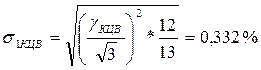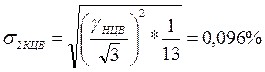Параметры экспоненциального распределения с α=0,5; k=1,35; χ=0,2;  ε=25,2.

Таким образом, все составляющие погрешности разделены на аддитивные и мультипликативные, им приписаны законы распределения и вычислены СКО. Этот результат для наглядности представлен на рисунке 3, где буквами А и М в кружках отмечены соответственно аддитивная и мультипликативная составляющие погрешности.

 

3.2.8 Основная погрешность аналогового регистратора задается его классом точности. Однако в отличие от датчиков, погрешность которых нормируется без запаса на старение, погрешность всех приборов согласно стандарту нормируется с 25%-ным запасом на старение, т. е. фактическая погрешность нового прибора составляет не больше чем 0,8γ_кл. Если прибор уже ремонтировался, то его погрешность 0,4γ_кл. Благодаря этому приборам обеспечивается большой межремонтный срок службы, пока их погрешность возрастает от  0,4γ_кл до γ_кл. В среднем погрешность находящихся в эксплуатации приборов составляет 0,7γ_кл.

Предположим, что в рассматриваемом случае используется новый регистратор, и при классе точности 0,5 его погрешность составляет не более

γ рег max = 0,8 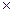 0,5 = 0,4 %.

Погрешность потенциометра определяется прежде всего погрешностью реохорда, поэтому она аддитивна, а закон ее распределения, как и у реостатного датчика, равномерный с шириной ±0,4 %. Тогда СКО этой погрешности

σ_рег = 0,4 / 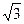 = 0,23%.

Параметры распределения: k = 1,73, χ = 0,745, ε = 1,8.

Температурная погрешность регистратора является аддитивной и проявляется в виде смещения нуля на ψΘ рег = − 0,1% 10 K . Максимальное значение погрешности при принятом выше равномерном законе распределения температуры шириной ±3 ^оС (±3 K) составляет

γ_{Θрег max} = ψ _{Θ рег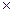}  3 K = 0,01  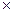3 K = 0,03%,

а ее СКО σ_{Θ рег} = 0,03/ 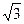 = 0,017 %.

Параметры распределения: k = 1,73, χ = 0,745, ε = 1,8.

 

3.2.9 Произведем суммирование погрешностей, т. е. расчет результирующей погрешности канала. Результирующая погрешность канала сводится к вычислению приведенной погрешности при Х = 0 (которая складывается из аддитивных составляющих) и в конце диапазона (которая складывается из всех составляющих - аддитивных и мультипликативных).

Выбор метода суммирования (алгебраического или геометрического) зависит от того, являются ли суммируемые погрешности коррелированными или независимыми. Следовательно, целесообразно сразу выделить коррелированные погрешности и произвести их алгебраическое сложение. Коррелированными являются те погрешности, которые вызываются одной и той же общей причиной, а поэтому имеют одинаковую форму закона распределения, которая остается и для их алгебраической суммы.

В данном примере это погрешность датчика Д и усилителя У от колебаний напряжения питания U, имеющая треугольный закон распределения, а также погрешность У и ЦВ от колебаний температуры в лаборатории, имеющая равномерный закон распределения. Однако погрешность от колебания температуры Датчика и Усилителя - это некоррелированные погрешности, так как их вызывают разные температуры (в цехе и в лаборатории). Для алгебраического суммирования коррелированных погрешностей необходимо установить их знаки. Так, коэффициент влияния на погрешность К_у от колебаний напряжения питания является положительным

 

ψ_{U у} =+0,3%/(10% ∆U/U),

 

т.е. коэффициент усиления с ростом напряжения питания возрастает. Также положительным является коэффициент влияния на погрешность от колебания напряжения питания датчика. Поэтому результирующее значение этих погрешностей просто равно их сумме 

 

σ_U(Д+У) = σ_{U Д} +σ_{U У} = 0,245+0,184 = 0,429 = 0,43%,

 

а закон распределения этой суммарной погрешности остается треугольным.

Уточним правила пренебрежения малыми составляющими при геометрическом суммировании погрешностей. Можно пренебречь одной составляющей, если она в 5 раз меньше наибольшей из суммируемых составляющих; двумя составляющими, если они в 6 раз меньше наибольшей из суммируемых составляющих, тремя составляющими, если они в 7 раз меньше. Но возможно делать только после суммирования коррелируемых составляющих и приведенных числовых значений погрешности к СКО.

В данном случае погрешность начала диапазона канала будет складываться из двух составляющих погрешности ЦВ (с равномерным распределением с σ _1НЦВ = 0,278% и с экспоненциальным распределением σ _2НЦВ = 0,080%) и погрешности Датчика с равномерным распределением и σ _Д = 0,087%. Составляющими же σ_θД = 0,026% и σ_θУ = 0,034% можно пренебречь, так как даже большая из них в 8 раз меньше, чем σ _1НЦВ = 0,278%.

Начнем суммирование с двух равномерно распределенных составляющих:

 

σ _Д+ЦВ  =  = .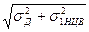

 

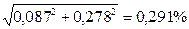Вес дисперсии второй составляющей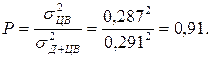

Эксцесс этого распределения составит

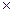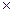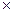σ _Д+ЦВ = ε ( x ) p ² +6 p  (1- p )+ ε ( y ) 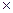(1- p ² ) = 1,8 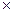0,91² + 6 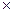0,91 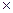 (1 -0,91) + 1,8  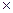(1 - 0,91² )= 2,0

 

Контрэксцесс распределения χ _Д+ЦВ 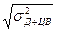= 1/  = 1/ 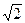 = 0,7. По кривой 3 (рисунок 2а) определим значение энтропийного коэффициента k _Д+ЦВ = 1,83.

Для суммирования этого распределения с экспоненциальной составляющей погрешности Р с α =0,5 и k =1,35 соответствующей кривой на рисунке 2а нет. На рисунке 2б при Р = 0 она должна начинаться в точке k =1,83, а заканчиваться при Р=1 в точке k = 1,35. При Р= 0,1-0,2 она пойдет вверх, как и все кривые на рисунке 2б, но достигает максимума в области при Р>0,3 аналогично кривой 4 (рисунок 2а), имеющей максимум при Р=0,7. Этот максимум не должен превышать k =2,02 , характерного для максимума кривой 3 на рисунке 2а, а спад ее в области Р=0,9-1 должен быть аналогичен спаду кривых 4 и 5 на рисунке 2б. Этих соображений достаточно, чтобы ориентировочно провести эту кривую. СКО погрешности в начале диапазона канала

 

σ_Д+ЦВ  =  = .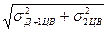

 

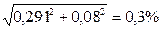Вес экспоненциальной составляющей 

 

 

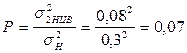
Эксцесс этого распределения ε_н = 2 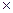0,07² + 6  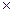0,07 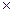 0,93 + 25,2  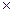0,995 = 25,47. Контрэксцесс χ = 1/  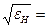0,198. Отсюда значение энтропийного коэффициента по построенной нами кривой составляет k _н = 2,02 и энтропийное значение погрешности в начале диапазона канала с цифровым вольтметром γ_н =k_н 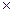σ_н = 2,02  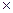0,302 = 0,61 %.

Для определения погрешности в конце диапазона канала нужно к составляющим погрешности ЦВ в конце диапазона с равномерным (σ_1КЦВ= 0,332%) и экспоненциальным (σ _2КЦВ = 0,096%) распре­делением   прибавить мультипликативные погрешности от колебаний напряжения питания (σ_U(Д+У)= 0,429%) с треугольным распределением и погрешностью от наводки (σ_нав = 0,16 %) с арксинусоидальным распределением. В данном случае погрешностью датчика можно пренебречь, так как отношение

σ_U(Д+У) / σ_У = 5.

Просуммируем сначала самые низкоэнтропийные из этих составляющих ( σ _нав = 0,16% с k _нав = 1,11 и σ_2ЦВ = 0,96% с k_2ЦВ=1,35) σ_нав+2ЦВ =  [0,16 ² + 0,096 ²]^-0.5 =0,187% .

Вес дисперсии экспоненциальной составляющей составит

 

 

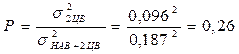
Эксцесс найдем как ε _НАВ+2ЦВ = 1,5 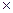 0,74² + 6  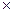0,74 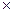 0,26 + 25,2  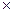0,932 =25,47. Контрэксцесс будет составлять

 

χ =1/ 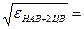 0,198.

 

Для определения значения энтропийного коэффициента воспользуемся кривой 4 (рисунок 2а), соответствующей суммированию арксинусоидальной ( k =1,11) и равномерной (k =1,73) составляющих. Нужная кривая в своей начальной части совпадает с этой кривой, а при Р→1 проходит несколько ниже. При малых значениях Р (Р=0,26) расхождение будет малым. Отсюда k _НАВ+2ЦВ=1,94. Теперь возьмём треугольное распределение с σ _U=0,429% и k _U =2,02 и сложим с ним полученную составляющую. Вес дисперсии второй составляющей Р= =0,48/0,2188 = 0,16.

Эксцесс ε _{U +НАВ+2ЦВ} = 2,4 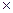 0,84² + 6 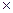0,84 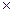 0,16 +3,7  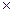0,16² = 2,6

и соответственно контрэксцесс χ = 0,62

При столь малом весе второй составляющей для суммирования можно воспользоваться начальным участком кривой 2 рисунка 2б), откуда найдем k_{U+нав+2ЦВ}=2,04.

Последнее суммирование будем рассматривать как сложение равномерно распределённой составляющей σ _1КЦВ = 0,332 % с близкой к нормальной составляющей с k=2,04. СКО погрешности в конце диапазона

 

 

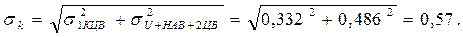
Вес близкой к нормальному распределению составляющей равен

 

 

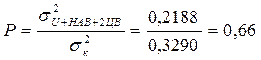
Эксцесс составляет ε _к = 1,8 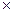 0,34² + 6  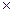0,34 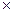 0,66 + 2,6  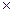0,66² = 2,7; контрэксцесс - χ _к =0,61.

На кривой 2 (рисунок 2а) такому весу соответствует энтропийный коэффициент, почти совпадающий с k нормального распределения, то есть будет близок к k =2,04. Энтропийное значение погрешности в конце диапазона будет равно

γ_к = k _к 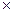 σ_к = 2,04  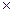0,57 = 1,2%.

Общая формула для вычисления приведенной погрешности результатов измерения при любом Х может быть записана

 

.

 

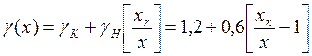Пределы допускаемых погрешностей канала при его ежегодных поверках сделаем не менее чем с 25%-ным запасом по отношению к вычисленным погрешностям. Для внесения в официальные документы в соответствии с ГОСТ 8.401-80 класс точности канала должен быть указан как 1,5/1,0.