Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Эти задачи относятся к трехфазным электрическим цепям переменного тока.

В трехфазных цепях потребители соединяют по схеме «звезда» или треугольник

Для её решения необходимо изучить материал, изложенный в Л 1 гл7, Л 5 гл 16, Л 7 гл 12, Л 8 гл 20, 21.

 

Параллельное подключение приемников энергию, соединенных звездой и треугольником, к трехфазной цепи.

Четырехпроводная трехфазная цепь позволяет присоединить:

а) трехфазные приемники к трем линейным проводам;

б) однофазные приемники между каждым линейным проводом и нейтральным.

 

Пример 3

В четырехпроводную сеть трехфазного тока (рисунок 18) с линейным напряжением U=380В включены по схеме "звезда" три группы электрических ламп накаливания одинаковой мощности. В каждой группе лампы соединены параллельно.

В среднем сопротивление одной лампы составляет 484Ом. Первая группа

 

 

 

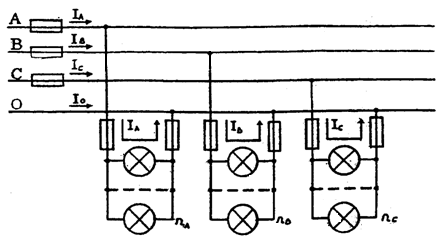
Рисунок 6 – Электрическая схема

 

Известны:

U _л ( U _АВ ; U _ВС ; U _СА ) - линейные напряжения;

Р_ламп – мощность одной лампы;

Р_а, Р_В, Р_С - мощности, потребляемые каждой фазой (группой ламп).

Определить:

U _ф ( U _А ; U _В ; U _С ) - фазные напряжения;

п_А; п_В; п_С  - число ламп в каждой фазе (группе);

I _А ; I _В ; I _С - фазные (они же линейные)токи;

Р-мощность, потребляемую цепью (всеми лампами).

Построить в заданных масштабах m_I и m_U векторную диаграмму напряжений и токов и из нее графически определить величину тока в нулевом проводе I ₀.

 

 На рисунке 18 показана трехфазная сеть, питающая две нагрузки, одна из которых соединена звездой, другая - треугольником. Система линейных напряжений симметрична U_АВ= U_ВС= U_СА=U_Л = 380 В.

Приемник энергии, соединенный звездой, имеет мощности фаз

Р_А = 2200 Вт; Р_Н = 3300 Вт; Р_С = 4400 Вт; коэффициент мощности

cos φ ^γ = 1(φ = 0⁰).

Приемник энергии, соединенный треугольником, - симметричный, мощности фаз Р_АВ = Р_ВС = Р_СА = 4260 Вт; cos φ ^∆ = 0.866 (φ ^∆ = 30⁰); характер нагрузки – активно – индуктивный.

Определить фазные и линейные токи нагрузок, токи в проводах линии, питающей обе нагрузки, и ток в нейтральном проводе.

 

 

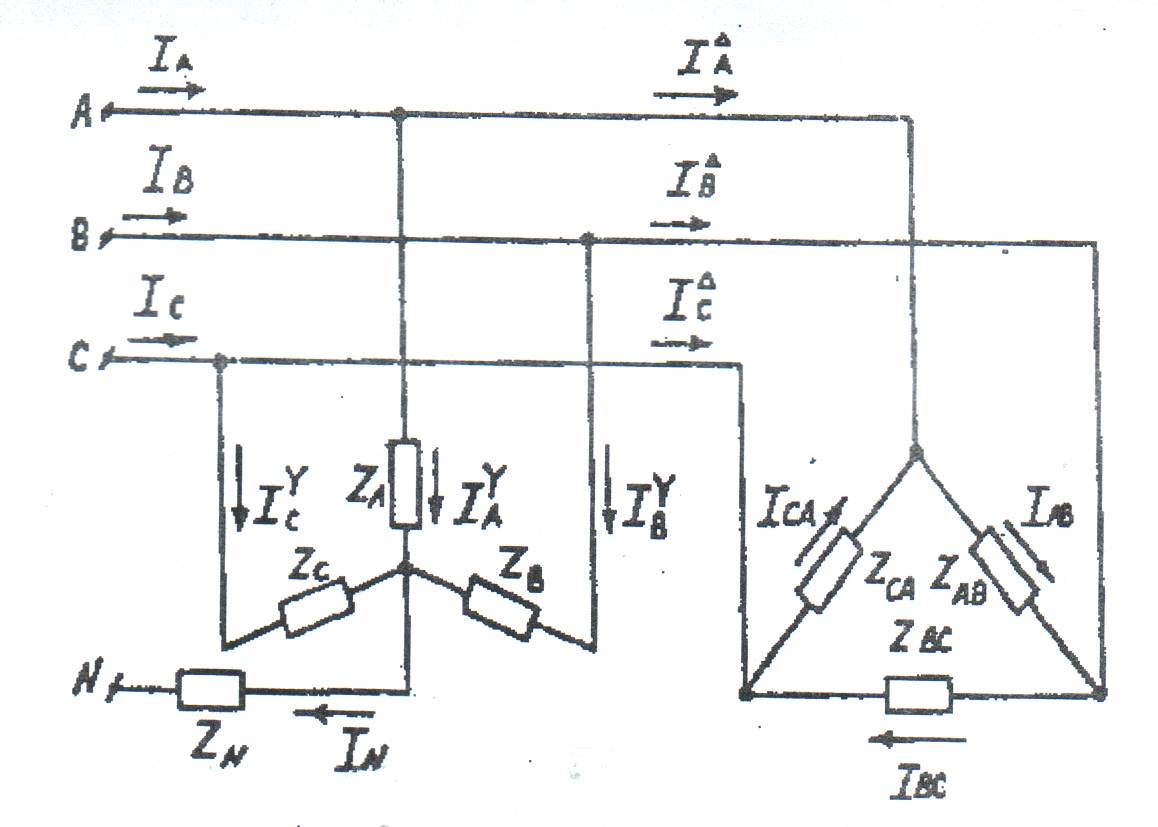
Рисунок 18-Трехфазная цепь

 

 

Решение

Фазные напряжения нагрузки, соединенной звездой, благодаря нейтральному проводу равны:

U_А = U_В = U_С =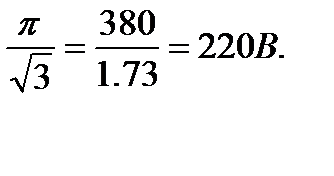

Фазные (линейные) токи нагрузки, соединенные звездой,

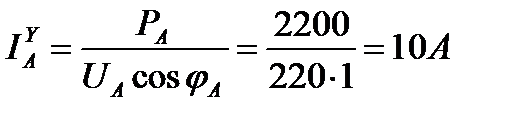
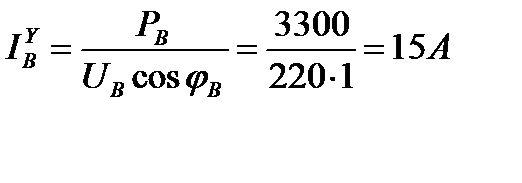
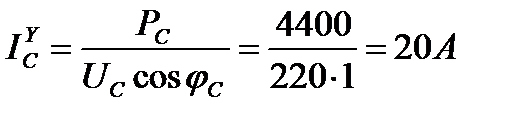
Согласно первому закону Кирхгофа для нейтральной точки N имеем:

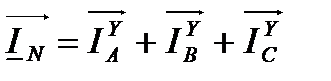
Следовательно, построив симметричную трехлучевую звезду фазных напряжений и отложив вдоль этих напряжений соответствующие фазные точки (так как 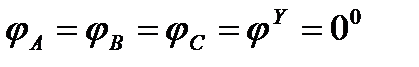, поскольку 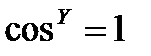), можно, геометрически сложив эти токи, определить вектор тока  в нейтральном проводе (см. рисунок 19).

 

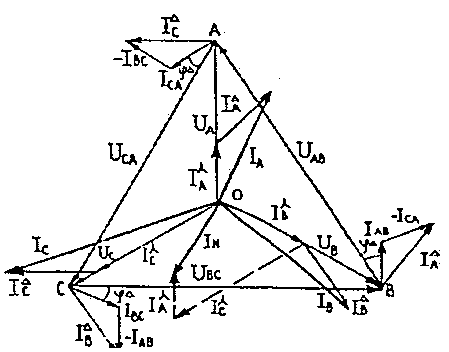
Рисунок 19-Векторная диаграмма

 

 

Зададимся масштабами m_u и m_{i .}

Производим указанное построение и графическим путем определяем

Согласно условию задачи трехфазный приемник, соединенный треугольником, - активно-индуктивный и, следовательно, фазные токи 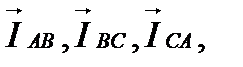отстают по фазе относительно вызывающих их напряжений  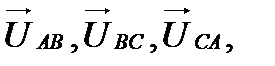соответственно на угол 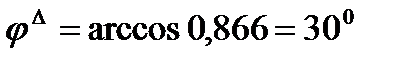. По величине эти фазные точки равны

 

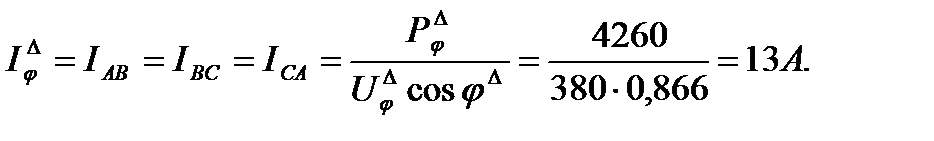
причем

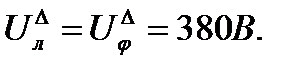
Соблюдая условия сдвига, длины векторов и выбранный масштаб токов m₁, производим построение векторов фазных токов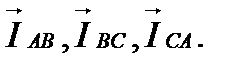

На основании первого закона Кирхгофа, примененного в узловых точках-вершинах треугольника, имеем:

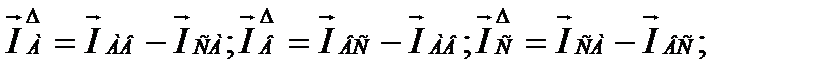
На основании этих равенств строим векторы линейных токов нагрузки, соединенной треугольником.

При симметричной нагрузке в фазах треугольника линейный ток больше фазного в 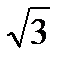раз и отстает на 30⁰ по фазе о первого из двух составляющих фазных токов

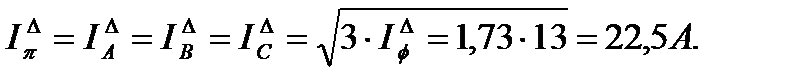
Проверка с помощью векторной диаграммы, например, 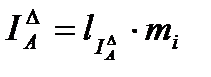 и т.д.

Суммарные токи в проводах линии, питающей обе нагрузки, определяют графическим путем на основании первого закона Кирхгофа

   

  

  

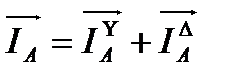
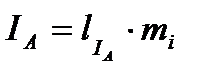
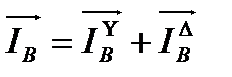
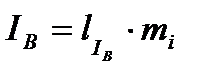
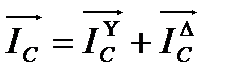
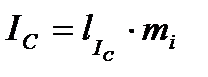
где l –длина вектора тока, получена из векторной диаграммы непосредственным измерением. Отсюда видно, что ток в нейтрально проводе непосредственно не фигурирует в выражениях суммарных линейных токов

ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ № 1

Задача 1.  Перед решением задачи изучите методические указания к решению задачи 1 и примеры 1, 2, 3

На рисунке 20 изображена схема сложной электрической цепи: Е₁, Е₂ – э.д.с. источников энергии; R₀₁, R₀₂ – их внутренние сопротивления; R₁, R₂, R₃ – сопротивления резисторов. 

Числовые значения этих параметров указаны в таблице 5 

Начертить схему цепи; показать направление токов в ветвях. Определить токи ветвей I₁, I₂, I₃. Метод расчета указан в таблице.

Проверить решение методом узлового напряжения.

Составить уравнение баланса мощностей.

 

 

 

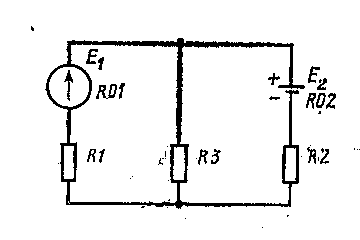
Рисунок 20-Электрическая схема

 

 

Таблица 5 - Исходные данные к задаче 1

№ вар	Е1, В	Е2, В	R01 , Ом	R02 , Ом	R1 , Ом	R2 , Ом	R3 , Ом	Метод расчета
1	100	90	2	1	18	9	14	Метод узловых и контурных уравнений
2	90	87	0,3	0,2	1,7	14	2,8	Метод контурных токов
3	120	56	0,2	0,1	4,8	2,8	6	Метод узловых и контурных уравнений
4	160	68	2	2	15	6	3,9	Метод контурных токов
5	210	80	0,5	0,5	4,5	3,9	4,5	Метод узловых и контурных уравнений
6	80	180	3	2	19	4,5	14	Метод контурных токов
7	85	135	1	1	17	14	13	Метод узловых и контурных уравнений
8	55	90	2	2	8	13	7	Метод контурных токов
9	105	120	2	3	18	7	13	Метод узловых и контурных уравнений
10	80	200	1	1	9	13	24	Метод контурных токов
11	110	120	0,4	1,7	14	24	6	Метод узловых и контурных уравнений
12	95	146	0,5	2,3	2,8	6	30	Метод контурных токов
13	76	34	1	1,5	6	30	17	Метод узловых и контурных уравнений
14	28	128	2	2	3,9	17	20	Метод контурных токов
15	120	60	0,5	0,3	4,5	20	30	Метод узловых и контурных уравнений
16	36	90	0,2	0,2	14	30	10	Метод контурных токов
17	40	46	0,3	2	13	10	12	Метод узловых и контурных уравнений
18	54	90	0,7	0,5	7	12	6	Метод контурных токов
19	45	87	0,9	3	13	6	50	Метод узловых и контурных уравнений
20	78	56	0,6	1	24	50	20	Метод контурных токов
21	100	68	2,5	2	6	20	13	Метод узловых и контурных уравнений
22	90	80	2	2	30	13	4,5	Метод контурных токов
23	120	180	1,7	1	17	4,5	6	Метод узловых и контурных уравнений
24	160	135	2,3	0,4	20	6	14	Метод контурных токов
25	210	90	1,5	0,5	30	14	30	Метод узловых и контурных уравнений
26	80	120	2	1	10	2,8	10	Метод контурных токов
27	85	200	0,3	2	12	1,7	12	Метод узловых и контурных уравнений
28	55	120	0,2	0,5	6	15	6	Метод контурных токов
29	105	146	2	2	50	4,5	50	Метод узловых и контурных уравнений
30	80	34	0,5	0,3	20	19	20	Метод контурных токов

 

Задача 2. Перед решением задачи изучите методические указания к решению задачи 2 и пример 4.

На рисунках 14. 15, 16 в однофазную электрическую сеть переменного синусои­дального тока включены активные и реактивные элементы, обладающие

сопротивления­ми.    

Определить: ток I в цепи;напряжение на каждом элементе цепи; активные, реактивные и полное сопротивления; угол сдвига фаз между напряжением и током ( по величине и знаку); активные и реактивные мощности элементов; активную, реактивную и полную мощности цепи.

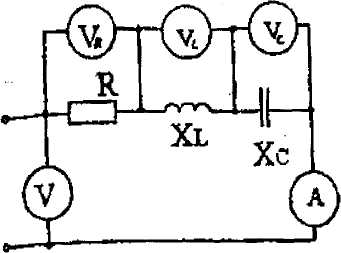
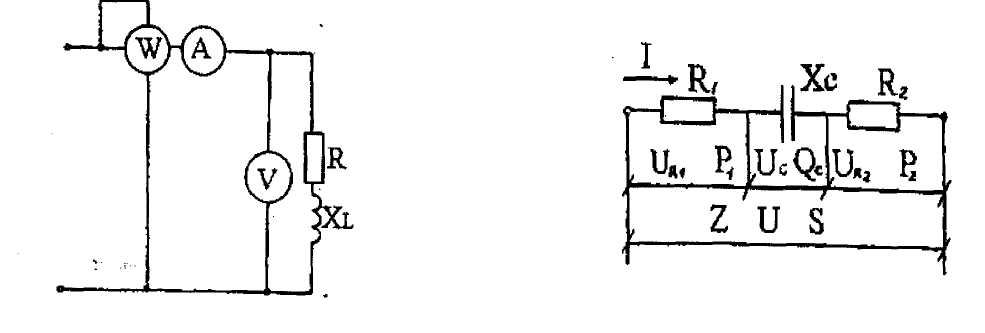
Рисунок 14

Рисунок 15

 

Рисунок 16

 

 

Построить в масштабе векторную диаграмму напряжений. После построения диаграммы измерить вектор суммарного напряжения и убедиться в том. что с учетом масштаба его величина равна напряжению, подведенному к зажимам цепи. Данные для своего варианта возьмите в таблице 6.

 

 

Таблица 6 - Исходные данные к задаче 2

 

№ вариант	№ рисунк	U , В	UR1 , В	UR 2 , В	I, А	Р, Вт	S , ВА	R , Ом	XL , Ом	XC , Ом
1	14	90	-	-	9	648	-	-	-	-
2	15	200	60	60	-	-	-	-	-	80
3	16	-	-	-	-	-	240	36	60	12
4	14	120	-	-	8	576	-	-	-	-
5	15	195	90	66	-	-	-	-	-	39
6	16	-	-	-	-	-	260	52	16	55
7	14	140	-	-	7	784	-	-	-	-
8	15	180	68	40	-	-	-	-	-	36
9	16	-	-	-	-	-	280	42	70	14
10	14	150	-	-	6	540	-	-	-	-
11	15	175	60	80	-	-	-	-	-	21
12	16	-	-	-	-	-	300	60	20	65
13	14	175	-	-	5	700	-	-	-	-
14	15	160	54	42	-	-	-	-	-	64
15	16	-	-	-	-	-	320	48	84	20
16	14	120	-	-	4	288	-	-	-	-
17	15	150	45	75	-	-	-	-	-	30
18	16	-	-	-	-	-	430	51	32	100
19	14	135	-	-	3	324	-	-	-	-
20	15	140	52	32	-	-	-	-	-	28
21	16	-	-	-	-	-	360	54	100	28
22	14	80	-	-	2	96	-	-	-	-
23	15	125	30	45	-	-	-	-	-	20
24	16	-	-	-	-	-	380	76	13	70
25	14	200	-	-	8	1280	-	-	-	-
26	15	170	70	32	-	-	-	-	-	68
27	16	-	-	-	-	-	400	60	120	40
28	14	200	-	-	4	528	-	-	-	-
29	15	165	48	84	-	-	-	-	-	33
30	16	-	-	-	-	-	440	88	33	99

 

 

Задача 3. Перед решением изучите методические указания к решению задачи 3 и пример 5.

На рисунке 11 показана трехфазная сеть, питающая две нагрузки, одна из которых соединена звездой, а другая – треугольником. Система линейных напряжений симметрична U_АВ = U_ВС = U_СА = U_л

    Определить:

а) фазные и линейные токи обеих нагрузок;

б) токи в проводах линии, питающей обе нагрузки;

в) ток в нейтральном проводе;

г) активную и реактивную мощности каждой из нагрузок и всей установки.

    В масштабе построить векторную диаграмму токов и напряжений.

Задачу решить графическим методом.

Все необходимые данные приведены в табл. 7.

Указания:

1. См. решение типовой задачи 2.

2. Нагрузка, коэффициент мощности которой cos φ не равен единице, имеет активно-индуктивный характер.                                                                                                                        

                                                                                                                                              

 

Таблица 7 - Исходные данные к задаче 3

 

Варианты

		Дата: 2018-12-21, просмотров: 1012. ⇐ Предыдущая12345678Следующая ⇒ Материалы представленные на сайте исключительно с целью ознакомления пользователям Интернета и не преследуют коммерческих целей или нарушение авторских прав. © 2018 - 2024