Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Эти задачи относятся к теме  ''Однофазные электрические цепи переменного синусоидального тока". В этих цепях, так же как и в цепях постоянного тока, при решении задач использует закон Ома, первый закон Кирхгофа, формулы мощности, свойства последовательного и параллельного соединений. Однако из-за того, что в переменном токе действует три вида совершенно различных по характеру сопротивлений (активное R, индуктивное Х_L и емкостное Х_C) форма записи законов изменяется. Иначе устанавливается связь и между однородными электрическими величинами. Так, при последовательном соединении в постоянном токе общее сопротивление было равно арифметической сумме сопротивлений, в переменном токе берется уже геометрическая сумма R, Х_L Х_C. Геометрически складываются также напряжения и мощности на этих сопротивлениях.

На основании закона Ома напряжения на активном, индуктивном и емкостном сопротивлениях могут быть определены по формулам: ; ;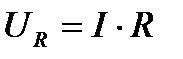

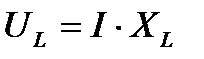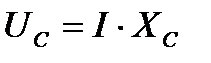
При этом следует иметь в виду, что 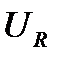 — совпадает по фазе с током,  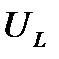-опережает по фазе ток на 90°,  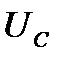- отстает от тока на 90°.

Результирующее напряжение 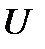представляет геометрическую сумму напряжени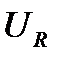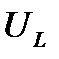и ,  и 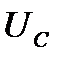. На рисунке 10 представлена векторная диаграмма этих напряжений.

 

 

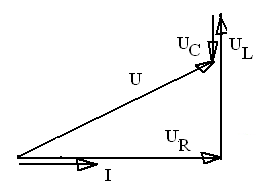
Рисунок 10-Векторная диаграмма

 

 

Результирующее напряжение U, которое является напряжением, подведенным к зажимам цепи, (можно найти не только графически в этом случае диаграмма должна быть построена в масштабе), но и математически, на основании теоремы Пифагора: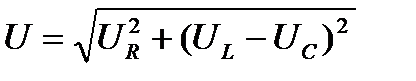

Если каждое из напряжений на векторной диаграмме (рисунок 10) разделить на ток I, то получится фигура, подобная векторной диаграмме, которая будет называться треугольником сопротивлений (рисунок 11) т.к.

; ;

 

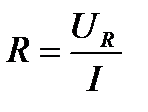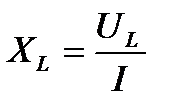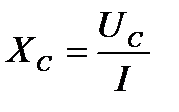
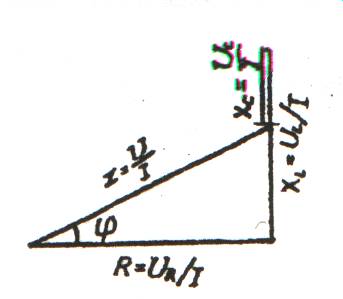
Рисунок11-Треугольник сопротивлений

 

Из треугольника сопротивлений следует, что

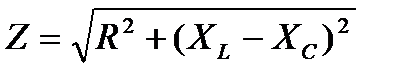
Если каждое из напряжений на векторной диаграмме (рисунке 10) умножить на ток I, то получится фигура, подобная векторной диаграмме, которая будет называться треугольником мощностей (рисунок 12), т. к. ; ;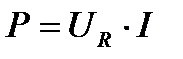  

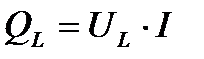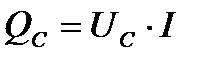
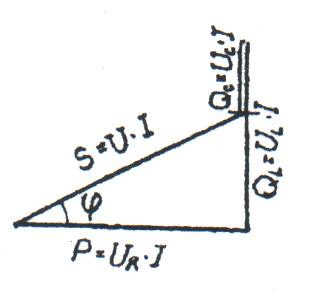
Рисунок 12- Треугольник мощностей

 

Из треугольника мощностей следует, что

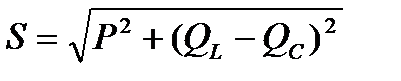
Используя закон Ома для каждого элемента цепи ток можно найти по формулам:

; ; ;

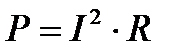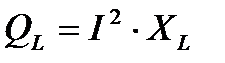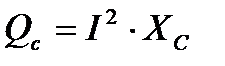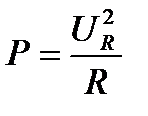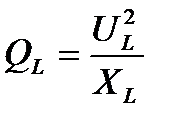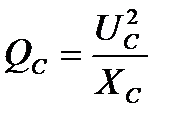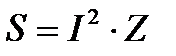; ; ;  или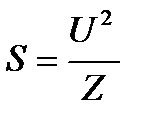

Из треугольника мощностей (рисунок 12) так же следует, что

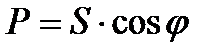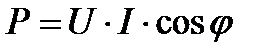
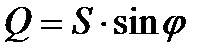 или

 или ,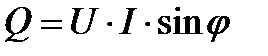

где 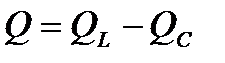  - результирующая реактивная мощность

Анализируя векторную диаграмму напряжений (рисунок 10), треугольник сопротивлений (рисунок 11), треугольник мощностей (рисунок12), можно сделать вывод что при U_L > U_C (Х_L> Х_C) результирующий вектор напряжения U опережает вектор тока I на угол φ <90°, а при U_L < U_C (Х_L < Х_C) результирующий вектор напряжения отстает от вектора тока на угол φ 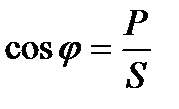 - называется коэффициентом мощности

Особенности расчета цепи при другой комбинации элементов схемы. При отсутствии одного из реактивных сопротивлений все электрические параметры определяются по вышеприведенным формулам. При этом из них нужно исключить параметры с индексом отсутствующего элемента.

 

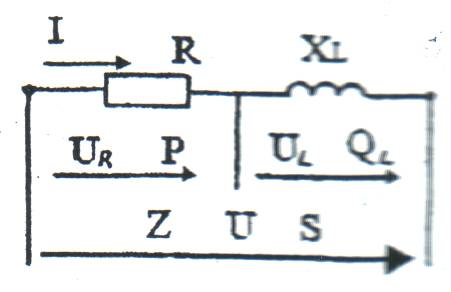
Рисунок 13-Электрическая схема

 

 

На рисунках 13 и 14 изображена цепь с последовательным соединением R и X_L, элемент X_С  отсутствует, поэтому ; ; ; ; ; ;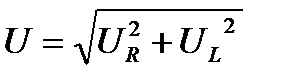

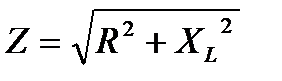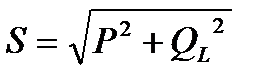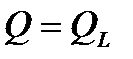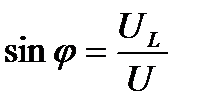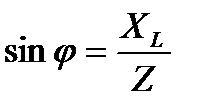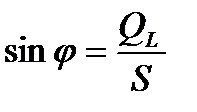
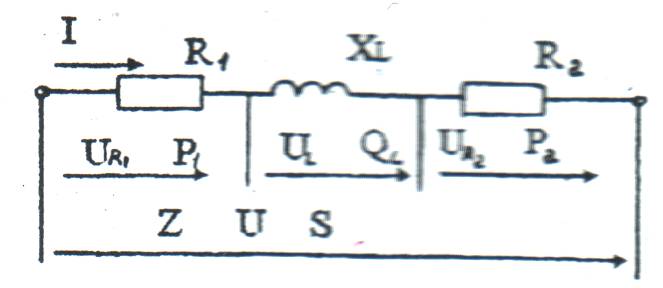
Рисунок 14-Электрическая схема

 

; ; ; ; ; .

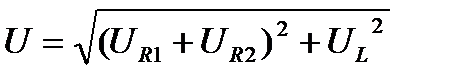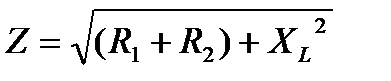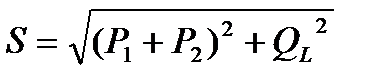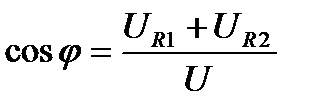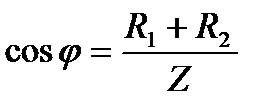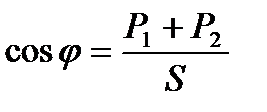Векторная диаграмма, треугольник сопротивлений и треугольник мощностей будут иметь вид, изображенный на рисунке 15

 

 

 

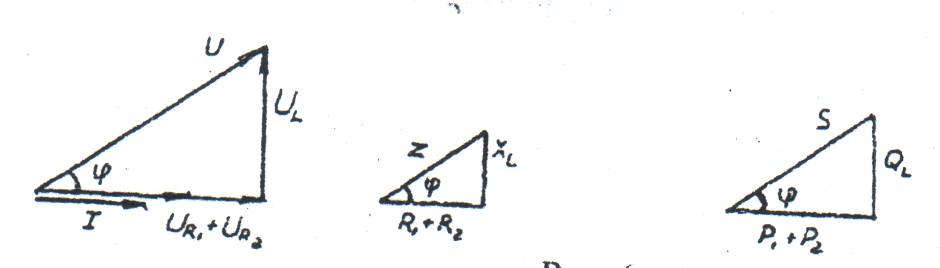
Рисунок 15-Векторная диаграмма

 

Пример 2

На рисунке 16 в однофазную электрическую цепь переменного синусои­дального тока напряжением U=50В включены активные R₁=9Ом и R₂=11Ом и реактивные элементы, обладающие сопротивления­ми Х_L = 12Ом, X_C =27Ом.

 

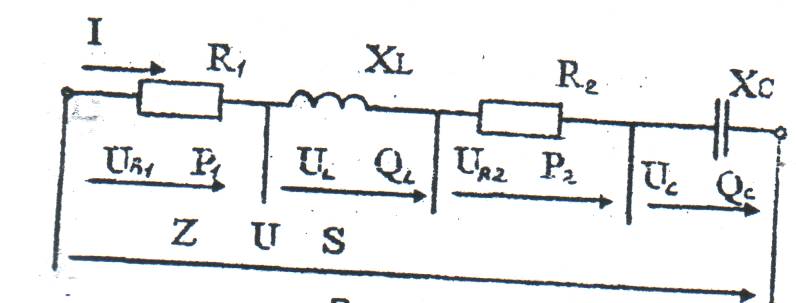
Рисунок 16-Электрическая схема

 

Определить: ток I в цепи; напряжение на каждом элементе цепи; активные, реактивные и полное сопротивления; угол сдвига фаз между напряжением и током ( по величине и знаку); активные и реактивные мощности элементов; активную, реактивную и полную мощности цепи.

Построить в масштабе векторную диаграмму напряжений. После построения диаграммы измерить вектор суммарного напряжения и убедиться в том, что с учетом масштаба его величина равна напряжению, подведенному к зажимам цепи

 

Решение

 

1. Определить полное сопротивление цепи

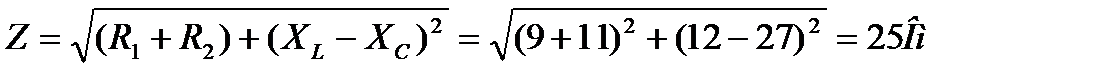
2. Определить ток цепи 

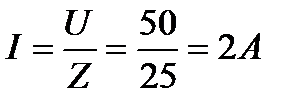
3. Определяем падение напряжения:

на активном сопротивлении R₁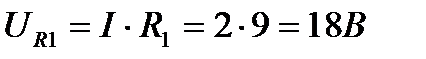

на активном сопротивлении R₂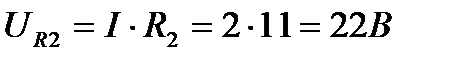

на индуктивном сопротивлении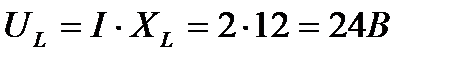

на емкостном сопротивлении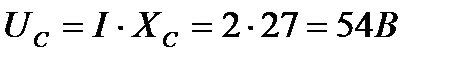

4. Определяем угол сдвига фаз между напряжением и током

;

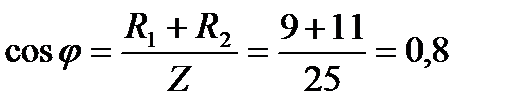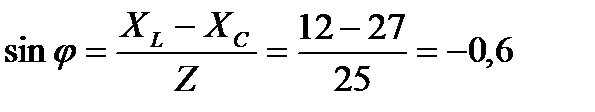
5. Определяем активную мощность цепи

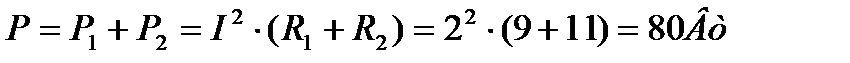
6. Определяем реактивную мощность цепи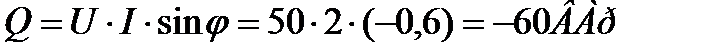

7. Определяем полную мощность цепи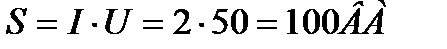

8. Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току и по напряжению ;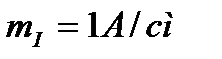

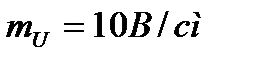
Здесь 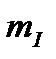 и 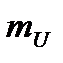 - масштабные коэффициенты. Они показывают, сколько ампер или вольт содержится в 1 см. Масштаб можно задавать и графически (см. рисунок 17).

 

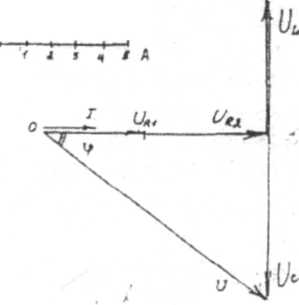
   Порядок построения

От точки 0 горизонтально вправо проводим вектор тока I общий для всей цепи. В выбранном масштабе его длина будет  

 

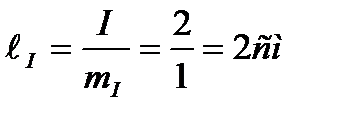
Рисунок 17-Векторная диаграмма

 

Вектор активного напряжения совпадает по фазе с током, угол сдвига фаз между ними равен 0, поэтому откладываем его вдоль вектора тока от точки 0 вправо. В выбранном масштабе его длина будет

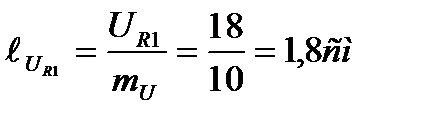
От конца вектора U_R1, откладываем вправо вдоль вектора тока вектор
активного напряжения U_R2. Его длина будет

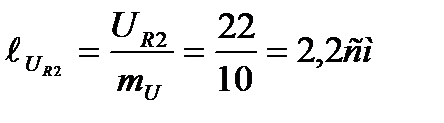
От конца вектора U_R2 откладываем вертикально вверх вектор падения напряжения на индуктивном сопротивлении U_L так как он опережает ток на угол 90°. Его длина будет

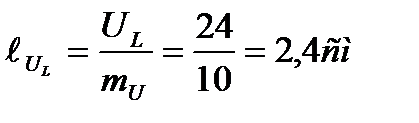
От конца вектора U_L  откладываем вертикально вниз вектор падения напряжения U_С на емкостном сопротивлении, т.к. он отстает от тока угол 90°. Его длина будет

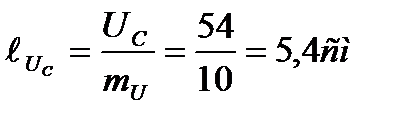
Геометрическая сумма векторов U_R1, U_R2, U_L и U_С должна быть равна полному напряжению U , приложенному к зажимам цепи, т.е.

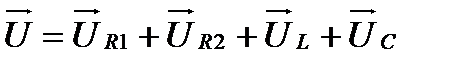
Измерив длину этого вектора, убеждаемся, что она l_U = 5 см. Это значит, что с учетом масштаба его величина будет: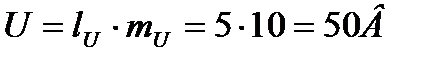

 По условию задачи именно такое напряжение приложено к зажимам

цепи.

Примечание:

Если в выбранном масштабе вектор суммарного напряжения не будет равен приложенному к зажимам цепи напряжению, то это будет говорить об ошибке, допущенной в решении задачи или в построении векторной диаграммы. Ее нужно найти и устранить:

Чаще всего наблюдаются ошибки, связанные с искажение масштабов при построении векторной диаграммы. Учтите это, при построении векторной диаграммы пользуйтесь чертежным инструментом. Выполняйте диаграмму точно и аккуратно.