Для составления схемы, в рабочей тетради начертить координатную сетку и оцифровать ее в масштабе 1:10000 с учетом координат исходных пунктов. Нанести по координатам пункты А, В, С, и по длинам линий с помощью измерителя и масштабной линейки, пункт Р.
Выбор наилучших вариантов засечки
Лучшими вариантами засечки считаются те, у которых углы при определяемой точке близки к 90° (определить визуально).
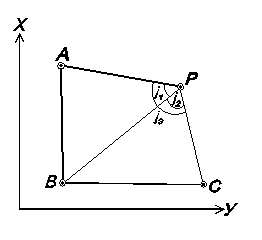
Рис. 10 – Схема построения для выбора лучших вариантов решения линейной засечки.
Решение наилучших вариантов засечки.
При решении данной задачи, прежде всего, необходимо определить длину стороны АВ по формуле:
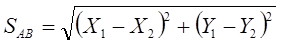 (2.12)
(2.12)
где: Х1, Х2, Y1, Y2 – координаты исходных точек.
Далее вычисляем основные коэффициенты:
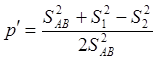 (2.13)
(2.13)
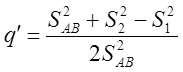 (2.14)
(2.14)
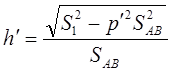 (2.15)
(2.15)
где: S1, S2 – длины измеренных линий.
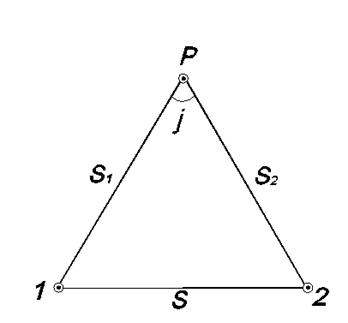
Рис. 11 – Схема обозначений к вычислениям по формулам (2.12-2.20)
Вычисляем координаты точки Р по формулам (2.16) и (2.17) с контролем правильности вычислений по формулам (2.18) и (2.19).
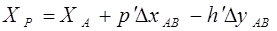 (2.16)
(2.16)
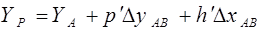 (2.17)
(2.17)
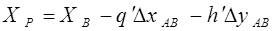 (2.18)
(2.18)
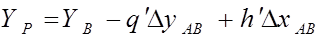 (2.19)
(2.19)
Расхождение координат вычисленной точки в приеме не должно превышать ошибок округления, то есть 0,01м.
Решить два наилучших варианта засечки, используя исходные данные и формулы (2.12-2.19). Вычисления произвести по схеме, приведенной в таблице 8.
Если расхождения координат в двух вариантах засечки не превысят 0,2 м (с учетом точности исходных данных) за окончательные значения координат принять их средние значения.
Схема для вычислений линейной засечки Таблица 8
| Название точки | координаты | приращения координат | Длина линии | коэффициенты | |
| X | Y | ||||
| А | XА | YА | ΔxАВ | S1 | p΄ |
| В | XВ | YВ | ΔyАВ | S2 | q΄ |
| Р’ | X (2.16) | Y (2.17) | SАВ | h΄ | |
| Р” | X (2.18) | Y (2.19) | |||
Оценка ожидаемой точности полученных результатов
Определить среднюю квадратическую ошибку положения точки Р для каждого варианта засечки по формуле:
 (2.20)
(2.20)
где: ms – средняя квадратическая ошибка измеренной стороны, γ – угол при определяемой точке.
Среднюю квадратическую ошибку измерянной стороны определить по формуле:
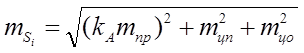 (2.21)
(2.21)
где: КА – коэффициент влияния атмосферных помех (принять КА = 2), 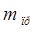 - средняя квадратическая ошибка измерения линии прибором (
- средняя квадратическая ошибка измерения линии прибором ( 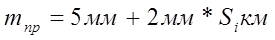 ),
), 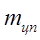 и
и 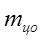 - средние квадратические ошибки центрирования прибора и отражателя (принять равными 10 мм.).
- средние квадратические ошибки центрирования прибора и отражателя (принять равными 10 мм.).
Среднюю квадратическую ошибку координат, полученных как средние значения из двух вариантов, вычислить по формуле (2.5).
Оформление работы.
Решение задачи определения координат пункта Р оформить на отдельных листах. При оформлении обязательно привести схему определения лучших вариантов решения данной задачи, таблицу вычисления координат точки Р и результаты оценки точности вычислений.
Лабораторная работа № 3.
Упрощенное уравнивание сетей триангуляции.
Приборы и инструменты: калькулятор.
Цель работы: изучение камеральной обработки геодезических измерений при уравнивании систем триангуляции 2 разряда.
Трудоемкость лабораторной работы 10 часов, в том числе 26 часов внеаудиторной работы.
3.1. Упрощенное уравнивание центральной системы.
3.1.1.Общие указания и исходные данные.
Центральной системой в геодезии принято называть такую систему треугольников триангуляции, которая имеет в своем составе точку, на которой измерянные углы образуют полный круг. Уравнивание центральной системы состоит в определении поправок к измерянным углам, уравненных координат точек и оценки точности геодезического построения. Данная методика уравнивания называется упрощенной потому, что решение возникающих в системе условных уравнений производится раздельно, по типам уравнений.
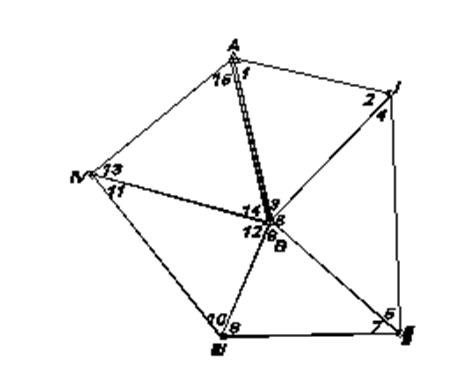
Рис. 12 – Схема центральной системы.
Исходные данные для решения центральной системы Таблица 9
| № угла | Угол | № угла | Угол | № угла | Угол | ||||||
| ˚ | ΄ | ˝ | ˚ | ΄ | ˝ | ˚ | ΄ | ˝ | |||
| 1 | 53 | 16 | 00+К1*Nв | 7 | 58 | 45 | 54+К2*Nв | 13 | 50 | 33 | 21+К3*Nв |
| 2 | 44 | 57 | 00+К2*Nв | 8 | 61 | 42 | 38+К4*Nв | 14 | 66 | 14 | 36+К1*Nв |
| 3 | 81 | 46 | 57+К3*Nв | 9 | 59 | 31 | 32+К3*Nв | 15 | 63 | 12 | 08+К2*Nв |
| 4 | 50 | 42 | 57+К1*Nв | 10 | 53 | 19 | 40+К2*Nв | ||||
| 5 | 43 | 27 | 39+К2*Nв | 11 | 57 | 00 | 29+К1*Nв | ||||
| 6 | 85 | 49 | 32+К3*Nв | 12 | 69 | 39 | 46+К3*Nв | ||||
Исходные координаты Таблица 10
| Исходный пункт | координаты | |
| Х | У | |
| А | 85443,47 | 30190,40 |
| В | 83659,97 + К5*Nв | 31146,19 + К6*Nв |
В таблицах 9 и 10, Nв - индивидуальный номер для студента, выдаваемый преподавателем, К1, К2, К3, К4, К5, К6 – коэффициенты, выдаваемые преподавателем для группы.
3.1.2.Общий порядок уравнивания центральной системы.
Подсчитать число возникающих в сети условных уравнений, разбить их по группам. Решить условные уравнения и вычислить уравненные углы. Вычислить длины всех сторон сети. Составить ходовую линию и вычислить координаты всех точек сети. Произвести оценку точности.
3.1.3.Порядок выполнения.
Подсчет числа и составление условных уравнений.
Составить схему уравниваемой сети. Подсчитать число измеренных углов и число определяемых пунктов. Вычислить число условных уравнений, возникающих в данной сети:
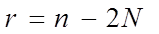 , (3.1)
, (3.1)
где: r – число условных уравнений, n – количество измерянных углов, N – количество определяемых пунктов сети.
Составление условных уравнений начинаем с уравнений фигур, в данном случае треугольников. Эти уравнения составляют первую группу.
(1) + (2) + (3) + W1 = 0 (3.2)
(4) + (5) + (6) + W2 = 0 (3.3)
(7) + (8) + (9) + W3 = 0 (3.4)
(10) + (11) + (12) + W4 = 0 (3.5)
(13) + (14) + (15) + W5 = 0 (3.6)
где: (1), (2), (3) и т.д. – поправки в измеренные углы, W – свободные члены уравнений, вычисляемые по следующим формулам:
W1 = 180˚ – 1 – 2 – 3 (3.7)
W2 = 180˚ – 4 – 5 – 6 (3.8)
W3 = 180˚ – 7 – 8 – 9 (3.9)
W4 = 180˚ – 10 – 11 – 12 (3.10)
W5 = 180˚ – 13 – 14 – 15 (3.11)
Вторая группа уравнений состоит из уравнения горизонта. Данное уравнение содержит поправки в углы измеренные при центральной точки.
(3) + (6) + (9) + (12) + (15) +W6 = 0, (3.12)
где: W6 = 360˚ – 3 – 6 – 9 – 12 – 15 (3.13)
Третья группа уравнений это уравнение полюса. Уравнение полюса для данной системы имеет следующий вид:
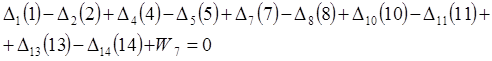 , (3.14)
, (3.14)
где: Δ – изменение шестого знака логарифма синуса угла при изменении угла на одну секунду,
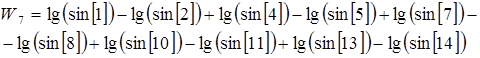 (3.15)
(3.15)
Решение условных уравнений
Решение данной задачи принято производить в таблице (см. таблица11). В таблицу выписать значения измеренных углов, по каждому треугольнику вычислить суммы углов и определить свободные члены уравнений первой группы (3.7 – 3.11). Поправки за уравнения первой группы распределить равномерно на все углы треугольника, в целых минутах таким образом, чтобы сумма поправок была равна свободному члену уравнения, взятому с противоположным знаком. Вычислить значения углов исправленных поправками уравнений первой группы.
Определить свободный член уравнения второй группы (3.13). Поправки за уравнения второй группы распределить равномерно на все углы, расположенные при центральной точке системы, в целых минутах таким образом, чтобы сумма поправок была равна свободному члену уравнения, взятому с противоположным знаком. Для компенсации влияния уравнения второй группы на уравнения первой ввести дополнительные поправки в остальные углы треугольника равномерно в целых минутах таким образом, чтобы сумма поправок была равна нулю. Вычислить значения углов исправленных поправками уравнения второй группы.
Вычислить десятичные логарифмы синусов углов входящих в уравнение третьей группы. Для простоты дальнейших вычислений прибавить к значениям логарифмов десять и округлить до седьмого знака после запятой. Определить свободный член уравнения третьей группы (3.15). Для вычисления поправок в уравнение вычислить коэффициент (3.16).
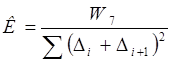 (3.16)
(3.16)
Величину поправки в углы вычислить по формуле:
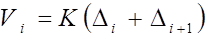 (3.17)
(3.17)
знак поправки определить из уравнения (3.14). Вычислить исправленные углы.
Оценку точности уравненного угла провести по формуле
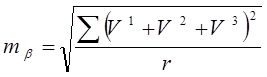 . (3.18)
. (3.18)
Примерная схема уравнивания центральной системы Таблица11
| № точки | Измеренный угол | V¹ | угол, уравненный первой группой поправок | V² | угол, уравненный второй группой поправок | lg(sin(i)) | Δ | V³ | Уравненный угол | ||||||||
| ˚ | ΄ | ˝ | ˚ | ΄ | ˝ | ˚ | ΄ | ˝ | ˚ | ΄ | ˝ | ||||||
| 1 | 53 | 16 | 00 | 1 | 53 | 16 | 01 | -1 | 53 | 16 | 00 | 9,9038644 | 1,6 | -2 | 53 | 15 | 58 |
| 2 | 44 | 57 | 00 | 1 | 44 | 57 | 01 | -1 | 44 | 57 | 00 | 9,8491057 | 2,1 | 2 | 44 | 57 | 02 |
| 3 | 81 | 46 | 57 | 1 | 81 | 46 | 58 | 2 | 81 | 47 | 00 | 81 | 47 | 00 | |||
| Σ | 179 | 59 | 57 | 3 | 180 | 00 | 00 | 0 | 180 | 00 | 00 | 3,7 | 0 | 180 | 00 | 00 | |
| 4 | 50 | 42 | 57 | -2 | 50 | 42 | 55 | -1 | 50 | 42 | 54 | 9,8887443 | 1,7 | -2 | 50 | 42 | 52 |
| 5 | 43 | 27 | 39 | -3 | 43 | 27 | 36 | -1 | 43 | 27 | 35 | 9,8374903 | 2,2 | 2 | 43 | 27 | 37 |
| 6 | 85 | 49 | 32 | -3 | 85 | 49 | 29 | 2 | 85 | 49 | 31 | 85 | 49 | 31 | |||
| Σ | 180 | 00 | 08 | -8 | 180 | 00 | 00 | 0 | 180 | 00 | 00 | 3,9 | 0 | 180 | 00 | 00 | |
| 7 | 58 | 45 | 54 | -1 | 58 | 45 | 53 | -1 | 58 | 45 | 52 | 9,9319878 | 1,3 | -1 | 58 | 45 | 51 |
| 8 | 61 | 42 | 38 | -1 | 61 | 42 | 37 | -1 | 61 | 42 | 36 | 9,9447590 | 1,1 | 1 | 61 | 42 | 37 |
| 9 | 59 | 31 | 32 | -2 | 59 | 31 | 30 | 2 | 59 | 31 | 32 | 59 | 31 | 32 | |||
| Σ | 180 | 00 | 04 | -4 | 180 | 00 | 00 | 0 | 180 | 00 | 00 | 2,4 | 0 | 180 | 00 | 00 | |
| 10 | 53 | 19 | 40 | 1 | 53 | 19 | 41 | -1 | 53 | 19 | 40 | 9,9042097 | 1,6 | -2 | 53 | 19 | 38 |
| 11 | 57 | 00 | 29 | 2 | 57 | 00 | 31 | -2 | 57 | 00 | 29 | 9,9236310 | 1,4 | 2 | 57 | 00 | 31 |
| 12 | 69 | 39 | 46 | 2 | 69 | 39 | 48 | 3 | 69 | 39 | 51 | 69 | 39 | 51 | |||
| Σ | 179 | 59 | 55 | 5 | 180 | 00 | 00 | 0 | 180 | 00 | 00 | 3,0 | 0 | 180 | 00 | 00 | |
| 13 | 50 | 33 | 21 | -1 | 50 | 33 | 20 | -1 | 50 | 33 | 19 | 9,8877511 | 1,7 | -1 | 50 | 33 | 18 |
| 14 | 66 | 14 | 36 | -2 | 66 | 14 | 34 | -2 | 66 | 14 | 32 | 9,9615439 | 0,9 | 1 | 66 | 14 | 33 |
| 15 | 63 | 12 | 08 | -2 | 63 | 12 | 06 | 3 | 63 | 12 | 09 | 63 | 12 | 09 | |||
| Σ | 180 | 00 | 05 | -5 | 180 | 00 | 00 | 0 | 180 | 00 | 00 | 0,0000274 | 2,6 | 0 | 180 | 00 | 00 |
Вычисление длин сторон сети
После уравнивания углов центральной системы вычислить длины всех сторон сети. Длину исходной стороны определить по координатам исходных точек (3.18). Вычисление остальных сторон провести по теореме синусов. (3.19 - формула для вычисления стороны АI). Контролем правильности уравнивания и вычисления сторон служит определение длины исходной стороны. Относительная ошибка определения стороны (3.20) не должна быть больше 1 / 10000.
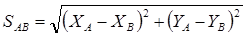 (3.19)
(3.19)
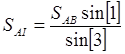 (3.20)
(3.20)
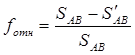 (3.21)
(3.21)
Вычисление координат точек сети
Перед началом вычисления координат всех точек сети проложить ходовую линию. Ходовая линия должна проходить через все определяемые точки сети, а начинаться и заканчиваться на твердых точках. По уравненным углам и вычисленным длинам линий составить ведомость вычисления координат и посчитать ее.
Оформление работы
Решение оформить на отдельных листах. При оформлении обязательно привести схему сети, таблицу уравнивания, ведомость вычисления координат и результаты оценки точности вычислений.
3.2. Упрощенное уравнивание цепочки треугольников с опорой на две отдельные твердые точки.
3.2.1.Общие указания и исходные данные.
Уравнивание цепочки треугольников с опорой на две твердые точки состоит в определении поправок к измерянным углам, уравненных координат точек и оценки точности геодезического построения.
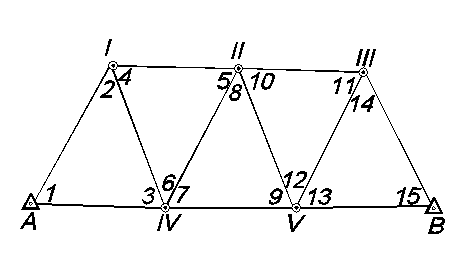
Рис. 13 – Схема цепочки треугольников.
Исходные данные для решения центральной системы Таблица 12
| № угла | Угол | № угла | Угол | № угла | Угол | ||||||
| ˚ | ΄ | ˝ | ˚ | ΄ | ˝ | ˚ | ΄ | ˝ | |||
| 1 | 53 | 19 | 53+К1*Nв | 7 | 81 | 46 | 39+К1*Nв | 13 | 84 | 45 | 15+К1*Nв |
| 2 | 69 | 39 | 37+К2*Nв | 8 | 44 | 57 | 15+К2*Nв | 14 | 45 | 47 | 06+К2*Nв |
| 3 | 57 | 00 | 20+К3*Nв | 9 | 53 | 15 | 49+К3*Nв | 15 | 49 | 27 | 13+К3*Nв |
| 4 | 50 | 32 | 56+К1*Nв | 10 | 61 | 40 | 36+К1*Nв | ||||
| 5 | 66 | 14 | 53+К2*Nв | 11 | 71 | 23 | 06+К2*Nв | ||||
| 6 | 63 | 12 | 05+К3*Nв | 12 | 46 | 55 | 52+К3*Nв | ||||
Исходные координаты Таблица 13
| Исходный пункт | координаты | |
| Х | У | |
| А | 31256,26 | 125689,21 |
| В | 39651,24+ К5*Nв | 125649,59+ К6*Nв |
В таблицах 12 и 13, Nв - индивидуальный номер для студента, выдаваемый преподавателем, К1, К2, К3, К5, К6 – коэффициенты, выдаваемые преподавателем для группы.
3.2.2.Общий порядок цепочки треугольников с опорой на две отдельные твердые точки.
Подсчитать число возникающих в сети условных уравнений. Решить условные уравнения и вычислить уравненные углы. Вычислить длины всех сторон сети. Составить ходовую линию и вычислить предварительные координаты всех точек сети. Определить поправку к начальному дирекционному углу и коэффициент масштабирования длин линий сети. Произвести оценку точности.
3.2.3.Порядок выполнения.
Подсчет числа и составление условных уравнений.
Составить схему уравниваемой сети. Подсчитать число измерянных углов и число определяемых пунктов. Вычислить число условных уравнений возникающих в сети (3.1).
Составить условные уравнения фигур, в данном случае треугольников.
(1) + (2) + (3) + W1 = 0 (3.22)
(4) + (5) + (6) + W2 = 0 (3.23)
(7) + (8) + (9) + W3 = 0 (3.24)
(10) + (11) + (12) + W4 = 0 (3.25)
(13) + (14) + (15) + W5 = 0 (3.26)
где: (1), (2), (3) и т.д. – поправки в измерянные углы, W – свободные члены уравнений, вычисляемые по следующим формулам:
W1 = 180˚ – 1 – 2 – 3 (3.27)
W2 = 180˚ – 4 – 5 – 6 (3.28)
W3 = 180˚ – 7 – 8 – 9 (3.29)
W4 = 180˚ – 10 – 11 – 12 (3.30)
W5 = 180˚ – 13 – 14 – 15 (3.31)
Решение условных уравнений
Решение данной задачи принято производить в таблице (см. таблица14). В таблицу выписать значения измерянных углов, по каждому треугольнику вычислить суммы углов и определить свободные члены уравнений (3.27 – 3.31). Поправки в углы распределить равномерно на все углы треугольника, в целых минутах таким образом, чтобы сумма поправок была равна свободному члену уравнения, взятому с противоположным знаком. Вычислить значения углов исправленных поправками уравнений.
Оценку точности уравненного угла провести по формуле
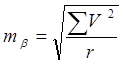 . (3.32)
. (3.32)
Вычисление длин сторон сети
После уравнивания углов вычислить длины всех сторон сети. Длину исходной стороны выбрать произвольно. Вычисление остальных сторон провести по теореме синусов. (3.19 - формула для вычисления стороны АI).
Вычисление координат точек сети
Перед началом вычисления координат всех точек сети проложить ходовую линию. Ходовая линия должна проходить через все определяемые точки сети, а начинаться и заканчиваться на одной из твердых точек. По уравненным углам, вычисленным длинам линий и произвольному начальному дирекционному углу составить ведомость вычисления координат и посчитать ее.
Используя вычисленные координаты твердой точки В и исходные координаты точки А вычислить дирекционный угол и длину стороны.
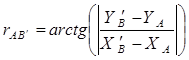 (3.33)
(3.33)
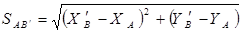 (3.34)
(3.34)
Аналогично вычислить точные значения дирекционного угла и стороны АВ, используя для этого исходные координаты пунктов.
Примерная схема уравнивания цепочки треугольников Таблица14
| № точки | Измеренный угол | V | Уравненный угол | S’ | ||||
| ˚ | ΄ | ˝ | ˚ | ΄ | ˝ | |||
| 1 | 53 | 19 | 53 | 3 | 53 | 19 | 56 | 1710,89 |
| 2 | 69 | 39 | 37 | 3 | 69 | 39 | 40 | 2000,00 |
| 3 | 57 | 00 | 20 | 4 | 57 | 00 | 24 | 1789,01 |
| Σ | 179 | 59 | 50 | 10 | 180 | 00 | 00 | |
| 4 | 50 | 32 | 56 | 2 | 50 | 32 | 58 | 1442,35 |
| 5 | 66 | 14 | 53 | 2 | 66 | 14 | 55 | 1710,89 |
| 6 | 63 | 12 | 05 | 2 | 63 | 12 | 07 | 1668,46 |
| Σ | 179 | 59 | 54 | 6 | 180 | 00 | 00 | |
| 7 | 81 | 46 | 39 | 5 | 81 | 46 | 44 | 2021,79 |
| 8 | 44 | 57 | 15 | 6 | 44 | 57 | 21 | 1443,35 |
| 9 | 53 | 15 | 49 | 6 | 53 | 15 | 55 | 1637,12 |
| Σ | 179 | 59 | 43 | 17 | 180 | 00 | 00 | |
| 10 | 61 | 40 | 36 | 8 | 61 | 40 | 44 | 1878,01 |
| 11 | 71 | 23 | 06 | 9 | 71 | 23 | 15 | 2021,79 |
| 12 | 46 | 55 | 52 | 9 | 46 | 56 | 01 | 1558,56 |
| Σ | 179 | 59 | 34 | 26 | 180 | 00 | 00 | |
| 13 | 84 | 45 | 15 | 8 | 84 | 45 | 23 | 2609,18 |
| 14 | 45 | 47 | 06 | 9 | 45 | 47 | 15 | 1878,01 |
| 15 | 49 | 27 | 13 | 9 | 49 | 27 | 22 | 1991,07 |
| Σ | 179 | 59 | 34 | 26 | 180 | 00 | 00 | |
По исходным и вычисленным дирекционным углам найти поправку в вычисленные дирекционные углы.
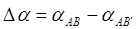 (3.35)
(3.35)
По исходным и вычисленным длинам сторон найти масштабный коэффициент.
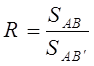 (3.36)
(3.36)
Составим новую ведомость вычисления координат. Исправим все ранее вычисленные дирекционные углы, прибавив к ним 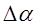 . Вычисленные в таблице 14 длины сторон умножим на масштабный коэффициент. Вычислим координаты всех точек сети. Контроль правильности вычислений заключается в получении координат точки В равных исходным.
. Вычисленные в таблице 14 длины сторон умножим на масштабный коэффициент. Вычислим координаты всех точек сети. Контроль правильности вычислений заключается в получении координат точки В равных исходным.
Оформление работы.
Решение оформить на отдельных листах. При оформлении обязательно привести схему сети, таблицу уравнивания, ведомость вычисления координат и результаты оценки точности вычислений.
Лабораторная работа №4.
Расчет номенклатуры и построение рамки листа карты масштаба 1:10000.
Цель работы: освоить методику определения номенклатуры трапеций средних масштабов, изучить зарамочное оформление листов трапеций.
Приборы и оборудование: калькулятор.
Трудоемкость лабораторной работы 8 часов, в том числе 8 часов внеаудиторной работы.
Исходные данные: широта (В) и долгота (L) точки, расположенной в определяемой трапеции (данные выдаются преподавателем).
Порядок выполнения работы.
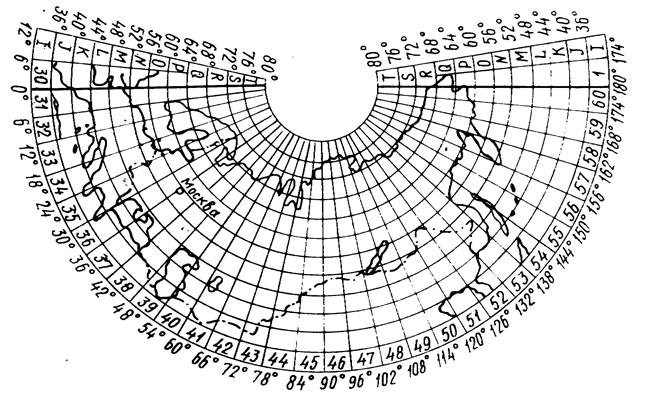
4.1. По широте и долготе точки определить номенклатуру листа карты масштаба 1:1000000 по схеме международной разграфки карт (Приложение В). По широте точки определить букву латинского алфавита, обозначающего ряд, а по долготе - номер колонны (Nк).
Установить значения широт и долгот углов трапеции масштаба 1:1000000 (Bю, Вс, Lз, Lв) и выписать их на схему (рисунок 14).
Для контроля найденных значений выполнить расчеты по следующим формулам:
| Nз = (L: 6° ) + 1 (4.1) | Lo = ( 6° * Nз ) - 3° (4.5) |
| Nк = Nз + 30 (4.2) | Lз = Lo - 3° (4.6) |
| Nр = (В: 4° ) + 1 (4.3) | Lв = Lo + 3° (4.7) |
Вс = 4° * Nр (4.4) Вю = Вс - 4° (4.8)
Пример решения приведен для точки с координатами: В=58°38’22”, L=60°53’45”. Вычислить номер шестиградусной зоны по формуле 4.2 и номер ряда по формуле 4.3. Согласно приложению А широтному ряду №15 соответствует буква латинского алфавита О.
Для рассматриваемого примера:
| Nз = ( 60°: 6° ) + 1 = 11 | Lo = ( 6° * 11 ) - 3° = 63° |
| Nк = 11 + 30 = 41 | Lз = 63° - 3° = 60° |
| Nр = ( 58° : 4° ) + 1 = 15 | Lв = 63° + 3° = 66° |
Вс = 4° * 15 = 60° Вю = 60° - 4° = 56°
Таким образом, окончательные значения основных параметров трапеции для рассматриваемого примера:
Nз = 11, номенклатура: О - 41, Вю = 56°,Вс = 60°,Lз = 60°,Lв = 66°.
4.2. Определить номенклатуру листа карты масштаба 1:100 000. Для этого на схеме (рисунок 13) лист карты масштаба 1:1 000 000 разделить на 144 разделительных листа карты масштаба 1:100000 и вычислить интерполированием широты и долготы разделительных параллелей и меридианов.
По широте и долготе точки определить номер листа карты масштаба 1:100000 и соответственно номенклатуру.
Для рассматриваемого примера искомая номенклатура О-41-50.
1.3. Определить номенклатуру листа карты масштаба 1:10000. Для этого на схеме (рисунок 14) лист карты масштаба 1:100000 разделить в последовательности по схеме:
4 листа 4 листа 4 листа
1:100000 ® 1:50000 ® 1:25000 ® 1:10000
А,Б,В,Г а,б,в,г 1,2,3,4
Вычислить интерполированием широты и долготы рамок трапеций масштаба 1:10000 и по заданным значениям широты и долготы установить искомую номенклатуру.
Для рассматриваемого примера номенклатура листа карты масштаба 1:10000 О-41-50-Б-б-1.
О – 41
| 60º00΄ | 66º00΄ | |||||||||||||||||
| 60º00΄ | 60º00΄ | |||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 40΄ | ||||||
| 13 | 24 | 20΄ | ||||||||||||||||
| 25 | 36 | 59º | ||||||||||||||||
| 37 | 48 | 40΄ | ||||||||||||||||
| 49 | 50 | 60 | 20΄ | |||||||||||||||
| 61 | 72 | 58º | ||||||||||||||||
| 73 | 84 | 40΄ | ||||||||||||||||
| 85 | 96 | 20΄ | ||||||||||||||||
| 97 | 108 | 57º | ||||||||||||||||
| 109 | 120 | 40΄ | ||||||||||||||||
| 121 | 132 | 20΄ | ||||||||||||||||
| 56º00΄ | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 56º00΄ | |||||
| 30΄ | 30΄ | 30΄ | 30΄ | 30΄ | 30΄ | |||||||||||||
| 60º00΄ | 61º | 62º | 63º | 64º | 65º | 66º00΄ | ||||||||||||
Рис. 14 – Деление трапеции масштаба 1:1 000 000.
О – 41 – 50
| 60º30΄ | 60º45΄ | 60º52΄30” |
| 61º00΄ |
| ||||||||||||||||||
| 58º40΄ | 60º56΄15” | 58º40΄ | |||||||||||||||||||||
|
| А | а | 1 | 2 | 58º40΄ |
| |||||||||||||||||
| 3 | 4 |
| 58º35΄ | ||||||||||||||||||||
| в | г |
| |||||||||||||||||||||
|
| 58º30΄ | ||||||||||||||||||||||
| В | Г |
|
| ||||||||||||||||||||
|
|
| ||||||||||||||||||||||
| 58º20΄ | |||||||||||||||||||||||
| 58º20΄ | |||||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||
| 60º45΄ |
|
| |||||||||||||||||||||
| 60º30΄ | 61º00΄ |
| |||||||||||||||||||||
Рис. 15 – Деление трапеции масштаба 1:100 000.
4.4. Вычислить прямоугольные координаты и сближение меридианов в проекции Гаусса-Крюгера для углов рамки трапеции масштаба 1:10 000.
Сначала по специальным таблицам [3] найти координаты и сближение меридианов для углов рамки трапеции масштаба 1:25 000, в которую входит трапеция масштаба 1:10 000. Выбор данных из таблицы [3] произвести по широте В и отклонению угла рамки от осевого меридиана
l = L - Lо. (1.9)
Найденные значения выписать на схему (рисунок 15). При расположении трапеции западней осевого меридиана ординаты и сближение меридианов будут иметь отрицательные значения. Затем вычислить прямоугольные координаты и сближение меридианов для углов рамки трапеции масштаба 1:10 000 линейным интерполированием между соответствующими значениями для углов рамки трапеции масштаба 1:25 000. Результаты интерполирования выписать на схему (рисунок 15).
О – 41 – 50 – Б – б
| lз = - 2˚ 07΄ 30˝ |
|
| lв = - 2˚ 00΄ 00˝ |
| |||||||||||||||
|
| 60˚ 52΄ 30˝ | 60˚ 56΄ 15˝ | 61˚ 00΄ 00˝ | ||||||||||||||||
| 58˚ 40΄ |
|
|
| ||||||||||||||||
|
x = 6 507 605.5 y = - 123 302.4 γ = - 1˚ 48΄ 55˝ |
x = 6 507 494.0 y = - 119 676.6 γ = - 1˚ 45΄ 43˝ |
x = 6 507 382.5 y = - 116 050.7 γ = - 1˚ 42΄ 31˝ | ||||||||||||||||
| 58˚ 35΄ |
x = 6 502 965.7 y = - 123 449.4
|
x = 6 502 854.1 y = - 119 819.2 γ = - 1˚ 45΄ 40˝ |
x = 6 502 742.5 y = - 116 189.2 γ = - 1˚ 42΄ 28˝ | ||||||||||||||||
|
x = 6 498 325.9 y = - 123 596.4 γ = - 1˚ 48΄ 49˝ |
x = 6 498 214.2 y = - 119 961.9 γ = - 1˚ 45΄ 37˝ |
x = 6 498 102.5 y = - 116 327.4 γ = - 1˚ 42΄ 25˝ | ||||||||||||||||
Рис. 16 – Схема вычисления прямоугольных координат углов трапеции масштаба 1:10 000.
В абсциссы углов, полученные при интерполировании, ввести поправку dх, которая приведена в приложении таблицы [3. с.510]. Поправка dх вводится с минусом, так как параллели в проекции Гаусса изображены дугами. Поправку вводить в точки расположенные на среднем меридиане трапеции масштаба 1:10 000.
Найденные значения масштаба 1:10000 занести в таблицу 1, предварительно преобразовав ординаты (прибавив 500 км) и указав впереди номер зоны. Например, если найденное значение У = -119676,6 м, то преобразованное значение У = 380323,4 м, а заносимое в таблицу 1.1, при Nз = 11, У = 11380323,4 м.
Таблица 15.
Координаты и сближение меридианов.
| Угол трапеции | Координат | Сближение Меридианов, g | |||
| Геодезические | прямоугольные Гаусса - Крюгера | ||||
| В | L | Х | У | ||
| СЗ | 58°40’00” | 60°52’30” | 6507605,7 | 11376697,6 | -1°48’55” |
| СВ | 58°40’00” | 60°56’15” | 6507492,3 | 11380323,5 | -1°45’43” |
| ЮЗ | 58°37’30” | 60°52’30” | 6502965,7 | 11376550,6 | -1°48’52” |
| ЮВ | 58°37’30” | 60°56’15” | 6502852,4 | 11380180,8 | -1°45’40” |
gср. = - 1°47’17,5”
Оформление работы.
Решение оформить на отдельных листах. При оформлении обязательно привести схемы деления листов карты и вычисления координат углов трапеции. а также таблицу окончательных значений основных параметров трапеции.
Вопросы для самостоятельного контроля
1. Опишите устройство и поверки теодолита 2Т5К.
2. Опишите устройство и поверки теодолита 3Т5КП.
3. Опишите технологию измерения горизонтальных углов теодолитом 2Т5К способом круговых приемов.
4. Дайте понятие прямой засечки.
5. Опишите выбор лучших вариантов решения прямой засечки.
6. Приведите описание решения прямой засечки по формулам Юнга.
7. Дайте понятие обратной засечки.
8. Опишите выбор лучших вариантов решения обратной засечки.
9. Приведите описание решения обратной засечки по формуле Деламбра.
10. Дайте понятие линейной засечки.
11. Опишите выбор лучших вариантов решения линейной засечки.
12. Приведите описание решения линейной засечки.
13. Приведите виды условных уравнений, возникающих при математической обработке сетей сгущения 2 разряда, построенных методом триангуляции.
14. Опишите упрощенное уравнивание и оценку точности центральной системы.
15. Опишите упрощенное уравнивание и оценку точности цепочки треугольников, опирающихся на два твердых пункта.
16. Дайте понятие картографических проекций.
17. Опишите номенклатуру листов карт средних масштабов.
Список рекомендуемой литературы
1. Куштин, И. Ф. Геодезия: учебно - практическое пособие / И. Ф. Куштин, В. И. Куштин. - Ростов н/Д : Феникс, 2009.- 909 с.
2. Маслов А.В. Геодезия: Учебное пособие для ВУЗов/ А.В. Маслов, А.В. Гордеев, Ю.Г. Батраков. – М.: Недра, 1993. -
3. Михелев Д. Ш. Геодезия : учебник / - М. : Академия, 2014. - 496 с.
4. Федотов Г.А. Инженерная геодезия: Учебное пособие для ВУЗов /Г.А. Федотов, - М.: Высшая Школа,2002. – 464 с.
5. Уставич, Г. А. Геодезия : в 2-х кн. : учебник. Кн. 1 / Г. А. Уставич ; Сиб. гос. геодез. акад. - Новосибирск : СГГА, 2012. - 352 с.
Приложение А.
Пример оформления журнала измерения углов способом круговых приемов.
Дата Время
Погода Ветер Изображение Наблюдал
| Название пункта | Название направ. |
Круг
Отчет
Средний отчет
Приведенный отчет
Среднее направление
Гео
Гео
95
4к
124
95
95
4к
124
95
Приложение Б
Схема международной разграфки листов карты масштаба 1:1 000 000
Дата: 2018-12-21, просмотров: 422.


 γ = - 1˚ 48΄ 52˝
γ = - 1˚ 48΄ 52˝