Для составления схемы, в рабочей тетради начертить координатную сетку и оцифровать ее в масштабе 1:10000 с учетом координат исходных пунктов. Нанести по координатам пункты А, В, С, и по углам, с помощью транспортира, пункт Р.
Выбор наилучших вариантов засечки
Для определения лучших вариантов засечки, на схеме построить инверсионные треугольники: для этого от пункта Р по направлениям РА, РВ, РС отложить отрезки (r), длину которых вычислить по формуле:
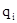 =
= 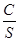 , (2.2)
, (2.2)
где: С – постоянное произвольное число, выбранное с таким расчетом, чтобы значения величины q были порядка 1-3 см; (С ≈ 10 см), S – расстояние от определяемого пункта до исходного, измеренное по схеме в сантиметрах.
Вершинами инверсионного треугольника для каждого варианта засечки будут являться пункт Р и конечные точки соответствующих отрезков qi.
Лучшими вариантами засечки считаются те, у которых наибольшие площади инверсионных треугольников (определить визуально).
Рисунок 4 - Схема построения инверсионных треугольников.
Решение наилучших вариантов засечки.
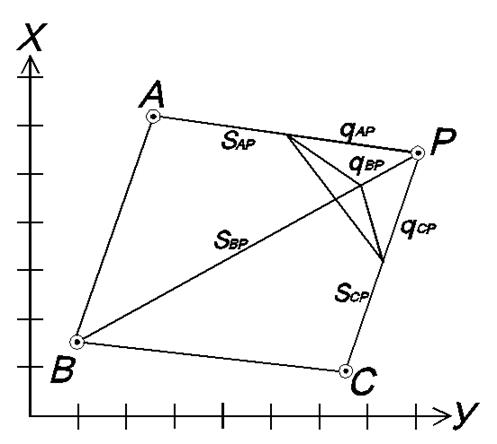
Рис. 4 – Выбор лучших вариантов обратной засечки.
Для решения вариантов засечки использовать следующие формулы Юнга:
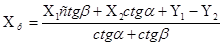 ,
, 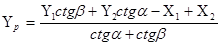 , (2.3)
, (2.3)
где Х1, Y1, Х2, Y2 - координаты исходных пунктов,
α, β - горизонтальные углы, измеренные на исходных пунктах.
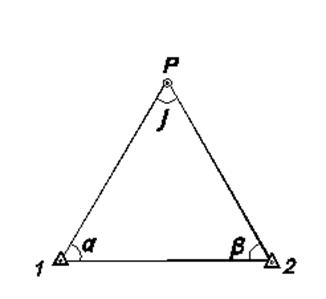
Рис. 5 - Схема к вычислениям прямой засечки по формулам (2.3).
В формулах (2.3) обозначения соответствуют схеме, приведенной на рисунке 5, при вычислении координат по второму варианту засечки следует применить те же обозначения.
Согласно варианту, используя формулы Юнга, вычислить координаты определяемого пункта Р, считая исходными пунктами сначала пункты А и В, а затем В и С. Расчеты свести в таблицу 3.
Таблица 3
Пример вычисления вариантов прямой засечки.
| Обозначения | Углы, º ′ ″
| Х, м | сtg α, ctg β, сtg α+ ctg β | Y,м | |
| пунктов | углов | ||||
| 1(А) 2(В) Р | α β | 87 41 20 44 19 20 | 8783,61 8084,10 8521,72 | 0,040358 1,023943 1,064301 | 4320,30 4069,80 4968,05 |
| 1(В) 2(С) Р | α β | 28 38 08 92 18 39 | 8084,10 8044,30 8521,74 | 1,831425 -0,040353 1,791072 | 4069,80 4926,53 4968,05 |
Среднее значение координат пункта Р: Х = 8521,73 м Y = 4968,05м
Оценка ожидаемой точности полученных результатов
Определить среднюю квадратическую ошибку положения точки Р для каждого варианта засечки по формуле:
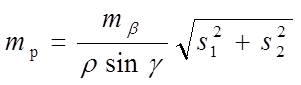 , (2.4)
, (2.4)
где mβ – средняя квадратическая ошибка измерения углов (принять в задании mβ = 10˝),
γ - угол в треугольнике при точке Р,
S1, S2 - стороны засечки, в м (определить по схеме),
Значение ρ принять в секундах (ρ =206265˝).
Среднюю квадратическую ошибку координат, полученных из двух вариантов засечки, найти по формуле:
Mpср= 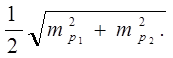 (2.5)
(2.5)
Оформление работы.
Решение задачи определения координат пункта Р оформить на отдельных листах. При оформлении обязательно привести схему определения лучших вариантов решения данной задачи, таблицу вычисления координат точки Р и результаты оценки точности вычислений.
2.2. Вычисление координат дополнительного пункта, определенного обратной многократной засечкой
2.2.1.Общие указания и исходные данные
Решение однократной обратной засечки заключается в определении координат четвертого пункта по трем исходным пунктам и двум углам, измеренным на определяемом пункте. С целью контроля правильности решения задачи на определяемом пункте производятся измерения углов, как минимум на четыре исходных пункта, т.е. засечка делается многократной.
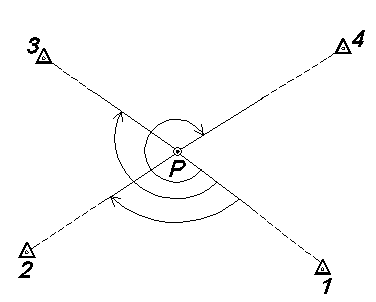
Рис. 6 - Схема обратной многократной засечки
Таблица 4
Исходные данные для решения обратной засечки
| Группы | Назв. пунктов | Координаты, м. | Измеренные на пункте Р направления º ′ ″ | |
| X | Y | |||
| 21 | 1 | 7104,51+0,20 № | 5851,55+0,12№ | 0º 00 ′00″ |
| 2 | 6613,06+0,20 № | 5816,43+0,12№ | 59 00 48 +1′ 27″ № | |
| 3 | 6652,86+0,20 № | 4959,70+0,12№ | 177 04 59 +3′ 42″ № | |
| 4 | 7352,37+0,20 № | 4210,20+0,12№ | 273 06 14 +1′ 06″№ | |
| 22 | 1 | 7114,61-0,60 № | 3841,45-0,25№ | 0º 00′ 00″ |
| 2 | 6623,16 -0,60 № | 3806,33-0,25№ | 60 14 58 -1′ 27″ № | |
| 3 | 6662,96–0,60 № | 2949,60-0,25№ | 180 13 31-3′ 41″ № | |
| 4 | 7362,47–0,60 № | 3200,10-0,25№ | 274 03 12-1′ 08″№ | |
В таблице 4, №-индивидуальный номер для каждого студента, выдаваемый преподавателем.
2.2.2.Общий порядок решения обратной многократной засечки.
Составить схему расположения определяемого и исходных пунктов, используя известные координаты и углы.
По схеме выбрать два наилучших варианта решения засечки путем сравнения площадей инверсионных треугольников.
Решить два выбранных варианта засечки. Расхождение координат, полученных в двух вариантах, с учетом точности измерений допускается до 0,2 м. При допустимом расхождении за окончательные значения координат принять их средние значения из двух вариантов.
Произвести оценку точности полученных координат определяемого пункта Р.
2.2.3.Порядок выполнения.
Дата: 2018-12-21, просмотров: 363.