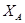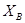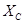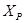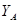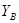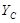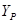Для составления схемы, в рабочей тетради начертить координатную сетку и оцифровать ее в масштабе 1:10000 с учетом координат исходных пунктов. Нанести по координатам пункты А, В, С, D и по способу Болотова (направлениям) пункт Р.
Выбор наилучших вариантов засечки
Если число исходных пунктов (направлений) в обратной засечке больше трех, то выбираются лучшие варианты ее решения из числа вариантов, рассчитываемых по формуле:
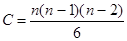 , (2.6)
, (2.6)
где n- число направлений.
Выбор лучших вариантов засечки производится так же, как в прямой засечке по площадям инверсионных треугольников, но вершинами в них будут только конечные точки отрезков qi.
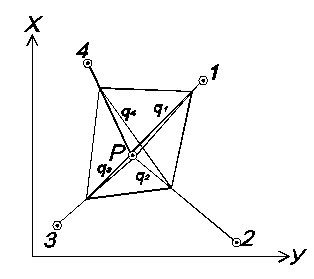
Рис. 7 - Схема построения инверсионных треугольников при выборе вариантов решения обратной засечки
Решение наилучших вариантов засечки
Обратная угловая засечка имеет множество способов решения. Для решения поставленной задачи сначала определить дирекционный угол одного из направлений (АР), принятого в качестве главного, по формуле Деламбра:

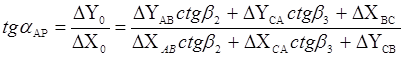 (2.7)
(2.7)

далее, определить дирекционный угол следующего направления:
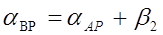 (2.8)
(2.8)
После определения дирекционных углов направлений АР и ВР, координаты определяемой точки вычислить по формулам Гаусса:
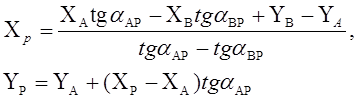 (2.9)
(2.9)
Для контроля вычислений вторично найти ординату определяемой точки по формуле:
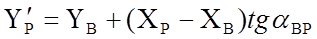 (2.10)
(2.10)
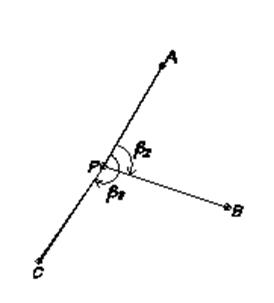
Рис.8 - Схема обозначений к вычислениям по формулам (2.7-2.11)
Решить два наилучших варианта засечки, используя исходные данные и формулы (2.7-2.10). Вычисления произвести по схеме, приведенной в таблице 5.
Если расхождения координат в двух вариантах засечки не превысят 0,2 м (с учетом точности исходных данных) за окончательные значения координат принять их средние значения.
Схема для вычислений обратной угловой засечки Таблица 5
| Обозначения пунктов | Координаты | - | 
| - | 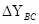
| |
|
А
В
С
Р |
|
| 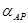
| - | tg 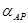
| - |
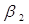
| 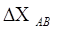
| ctg 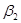
| 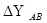
| |||
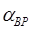
| - | tg 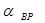
| - | |||
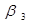
| 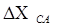
| ctg 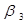
| 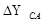
| |||
| - | 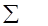
| - | 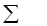
| |||
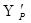
| 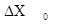
| tg 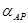 - tg - tg 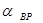
| 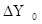
| |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Оценка ожидаемой точности полученных результатов
 Для оценки ожидаемой точности полученных координат по каждому варианту засечки применить формулу (обозначения согласно рисунку 8):
Для оценки ожидаемой точности полученных координат по каждому варианту засечки применить формулу (обозначения согласно рисунку 8):

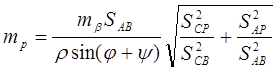 , (2.11)
, (2.11)
где:
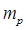 -средняя квадратическая ошибка положения определяемого пункта,
-средняя квадратическая ошибка положения определяемого пункта,
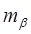 = 10²- средняя квадратическая ошибка измерения углов,
= 10²- средняя квадратическая ошибка измерения углов,
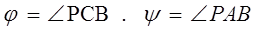 - углы, измеренные по схеме,
- углы, измеренные по схеме,
 - расстояния, измеренные по схеме (м)
- расстояния, измеренные по схеме (м)
Среднюю квадратическую ошибку координат, полученных как средние значения из двух вариантов, вычислить по формуле (2.5).
Оформление работы.
Решение задачи определения координат пункта Р оформить на отдельных листах. При оформлении обязательно привести схему определения лучших вариантов решения данной задачи, таблицу вычисления координат точки Р и результаты оценки точности вычислений.
2.3. Вычисление координат дополнительного пункта, определенного линейной многократной засечкой
2.3.1.Общие указания и исходные данные.
При решении линейной однократной засечки определяют координаты третьего пункта по известным координатам двух исходных пунктов и длинам линий, измеренным между определяемым и исходными пунктами. Для контроля правильности определения координат пункта засечку делают многократной, т.е. используют более двух исходных пунктов с измерениями на них, что заранее предусматривается в проекте работ. При этом число вариантов решения однократных засечек подсчитывают по формуле (2.1).
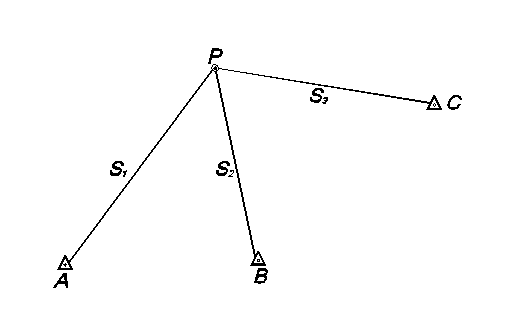
Рис. 9 – Схема линейной многократной засечки.
Исходные данные для решения линейной засечки Таблица 6
| Исходный пункт | координаты | Расстояние | |
| Х | У | ||
| А | 3676,45 | 3422,97 | 689,658+J |
| В | 3615,90+D | 4317,02+D | 730,791 |
| С | 2728,92 | 4370,50 | 679,877+J |
Значения индивидуальных поправок Таблица 7
| группы | Δ, м. | J, м. |
| 21 | 0,1 № | -0,026 № |
| 22 | -0,1 № | 0,026 № |
В таблице 7, № - индивидуальный номер для студента, выдаваемый преподавателем.
2.3.2.Общий порядок решения линейной многократной засечки
Составить схему расположения исходных и определяемого пунктов А, В, С и Р, используя известные координаты и длины линий.
По схеме выбрать два наилучших варианта решения засечки, путем сравнения углов, расположенных при определяемой точке, построенных треугольников.
Решить два выбранных варианта засечки, используя формулы для численного решения линейной засечки, расхождение координат, полученных в двух вариантах, с учетом точности измерений, допускается до 0,2 м. При допустимом расхождении за окончательные значения координат принять средние их значения из двух вариантов.
Произвести оценку точности полученных координат.
2.3.3.Порядок выполнения.
Дата: 2018-12-21, просмотров: 398.