Рассмотрим вынужденные колебания в последовательном контуре, изображённом на рис. 2.21. Будем рассматривать случай установившихся колебаний, когда все переходные процессы закончились, то есть после включения источника напряжения прошло достаточно много времени t >> 1/ δ .
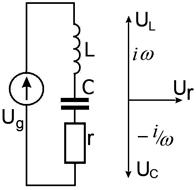
Рис. 2.21. Последовательный колебательный контур, возбуждаемый генератором переменного напряжения и комплексная диаграмма напряжений на элементах контура на резонансной частоте.
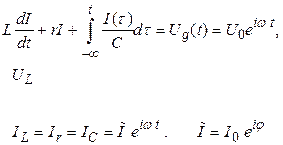Рассмотрим случай действия источника гармонических (синусоидальных) колебаний и напряжение источника запишем в комплексной форме U g (t) = U0 eiωt. Тогда:
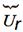(2.38)
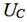Напряжения разные, а ток через элементы цепи одинаковый.
– комплексная величина. Она может быть сдвинута
по фазе относительно напряжения генератора.
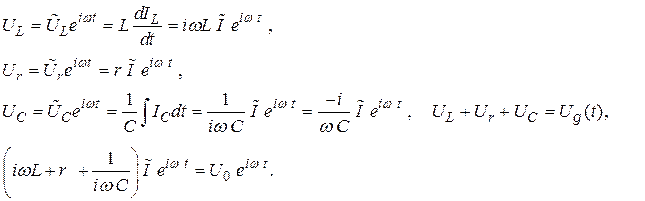
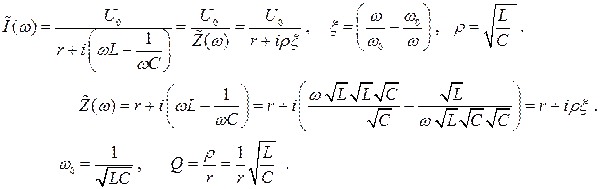
(2.39)
Здесь
где (2.40)
Здесь 
– импеданс последовательного колебательного контура, ξ – расстройка частоты, ρ – характеристическое или волновое сопротивление контура, Q – его добротность.
Физический смысл добротности Q будет рассмотрен ниже.
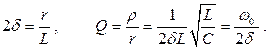
Кстати из (2.34): (2.41)
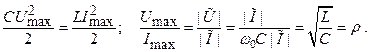Физический смысл волнового сопротивления контура в том, что это – отношение максимального напряжения на конденсаторе (или на индуктивности) к максимальному току. Проще всего получить это выражение через равенство максимальных энергий, запасённых
конденсатором и катушкой индуктивности.
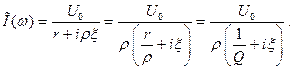
Из (2.39) : (2.42)
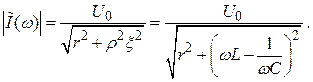
(2.43)
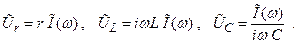Запишем комплексные амплитуды колебаний напряжений в виде:
(2.44)
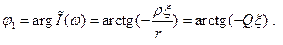
Из (2.42): (2.45)
Это – сдвиг фаз между напряжением на контуре и током. Сдвиг фаз зависит от частоты.
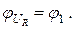
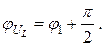Напряжение на сопротивлении не сдвинуто по фазе относительно тока:
Напряжение на индуктивности умножено на i (см. (2.44)), то есть
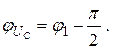
Напряжение на конденсаторе умножено на – i (2.44) и
См. диаграмму напряжений на рис. 2.21.
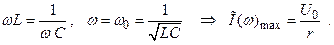Ток через контур максимален на резонансе, при условии:
Если в (2.43)
Здесь ω0 – резонансная частота, частота максимума тока.
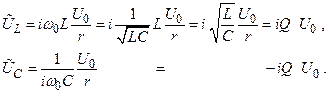На этой частоте напряжения на индуктивности и ёмкости равны и противофазны:
(2.46)
(2.47)
Сумма напряжений на ёмкости и индуктивности равна нулю на резонансной частоте, а импеданс контура минимален и равен r.
В этом случае фазы колебаний напряжений UL и UC таковы, что они компенсируют друг друга – это называется резонансом напряжений. Векторная диаграмма напряжений для этого случая приведена на рис. 2.21 справа.
На резонансе амплитуды напряжений UL и UC в Q раз больше напряжения генератора!
Если подавать на такой контур переменные напряжения с разными частотами, то контур будет выделять частоты, близкие к резонансной.
Напомним, что величина Q называется добротностью и для последовательного контура она равна отношению характеристического сопротивления ρ к сопротивлению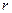 
.
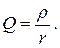
(2.48)
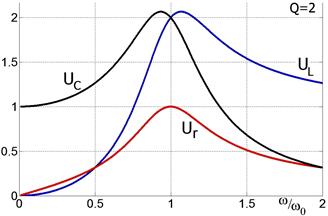
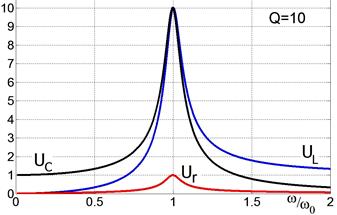
Рис. 2.22. Зависимости амплитуд вынужденных колебаний на ёмкости, сопротивлении и индуктивности для двух разных добротностей. При низкой добротности Q ~ 1 максимумы амплитуд разделяются. При добротностях Q >> 1 они почти совпадают. Напряжение на ёмкости при низкой частоте больше напряжения на индуктивности и равно напряжению на генераторе. На частотах выше резонансной напряжение больше на индуктивности. Соответственно изменится и вид векторной диаграммы на рис. 2.21. На максимумах напряжения на индуктивности и ёмкости равны и в Q-раз больше, чем напряжение на генераторе.
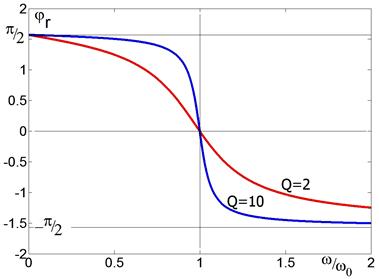
Рис. 2.23. Две фазовые характеристики, построенные по формуле (2.45) для разных добротностей. Это сдвиг фаз между напряжением на контуре и током.
Фазовые характеристики для напряжений на ёмкости и индуктивности просто сдвинуты вниз и вверх на π/2, см. (2.44).
Физический смысл добротности можно понять, если записать отношение запасённой в контуре энергии к энергии, теряемой за период.
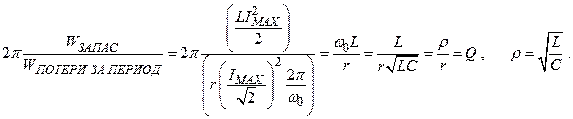
(2.49)
Последовательный контур можно использовать как полосовой фильтр, пропускающий частоты около резонанса. В радиоэлектронике принято характеризовать полосу граничными
частотами (на рис. 2.24 это частоты ω1 и ω2 ), при которых коэффициент передачи по модулю
падает до . Эти частоты определяются из уравнения:
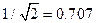
из ( 2.43)
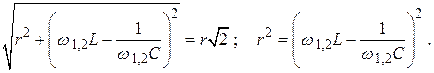
Отсюда: (2.50)
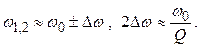
Решая уравнение (2.50), находим, что при Q >> 1 (2.51)
Заметим, что не каждому удаётся в уме решить даже квадратное уравнение и из (2.50) получить (2.51). Это решение приведено ниже. При первом чтении этот раздел можно пропустить.
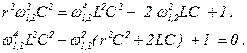
Из (2.50)
Окончательно:
из (2.49):
(2.52)
если Q >> 1, то: (2.53)
Если Q << 1, то (2.52) лучше переписать в таком виде:
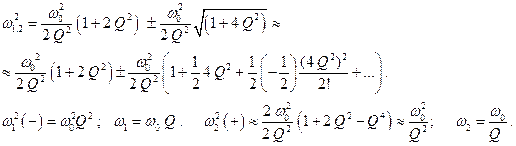
Сейчас пригодится третий член.
(2.54)
При выводе этой формулы пришлось учитывать и линейный, и квадратичный члены формулы бинома Ньютона.
Видим, что в случае малой добротности частоты ω1 и ω2 сильно различаются.
Величина добротности определяет полосу контура:
если Q >> 1, то или лучше (2.55)
Величину добротности контура по экспериментальной резонансной кривой можно вычислить, разделив резонансную частоту на ширину резонансной кривой на уровне 0.7.
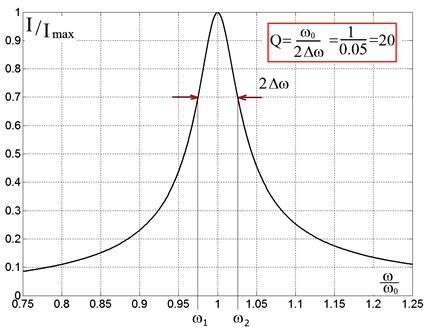
Рис. 2.24.
Резонанс тока в последовательном колебательном контуре с добротностью Q = 20.
График сосчитан по формуле (2.43) и нормирован на единицу.
Добротность, вычисленная по графику действительно равна 20!
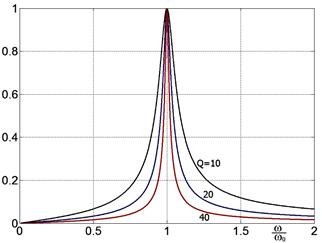
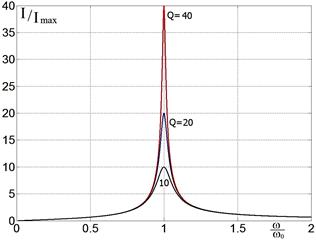
| Рис. 2.25. Резонансные кривые для токов в последовательном колебательном контуре с различными добротностями Q = 10, 20 и 40 сосчитаны по формуле (2.43). Видно, что токи на резонансной частоте в Q-раз больше. | Рис. 2.26. Те же резонансные кривые для токов в последовательном колебательном контуре с различными добротностями Q = 10, 20 и 40, но нормированные на единицу. Чем выше добротность, тем у́же резонансная кривая. |
Ток в последовательном контуре максимален на резонансной частоте. Значит, импеданс контура минимален на резонансе. На низких частотах импеданс емкостно́й, на высоких – индуктивный. На частоте, близкой к резонансной, его сопротивление минимальное и чисто омическое.
Пример – фильтр-пробка
Часто используют резонансные свойства контура для различных фильтрующих устройств, например как показано на рис. 2.27.
При условии ρ >> R i >> r схема на рис. 2.27 будет работать как фильтр-пробка, то есть сильно ослаблять переменное напряжение в полосе частот вблизи резонансной частоты, а напряжение вне полосы пропускать.
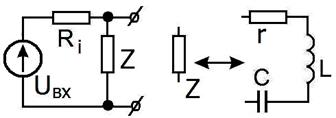
Рис. 2.27.
Схема фильтра-пробки.
Рассчитаем коэффициент передачи такой цепи:
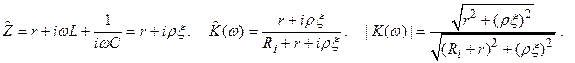Если Ri >> | 
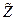( ω)|, то 
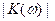→ 0. Если Ri <<| 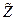( ω)|, то 
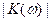→ 1.
(2.56)
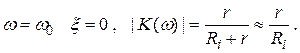
При
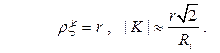
При
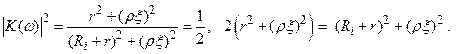
Вычислим частоты, на которых модуль коэффициента передачи уменьшается до уровня 0.7.
Так как Ri >> r , то: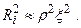 
(2.57)
Корень извлекать нельзя, так как расстройка бывает отрицательной (см. рис. 2.28).
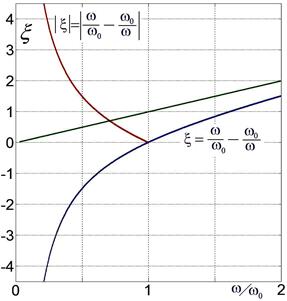
Рис. 2.28.
График зависимости расстройки ξ от круговой частоты ω.
Зелёная прямая линия – асимптота для больших частот.
Красная линия – график | ξ ( ω )| .
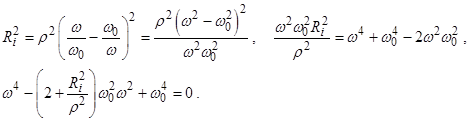
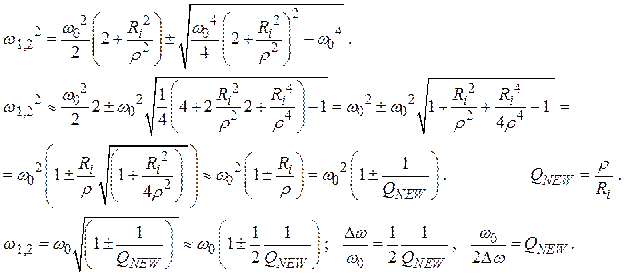
Здесь
(2.58)
2Δ ω – это ширина резонансной кривой на уровне 0.7, а QNEW – новая добротность – только для этой схемы.
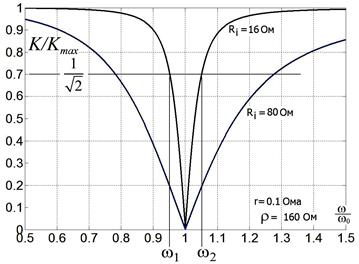
Рис. 2.29.
Зависимость нормализованного коэффициента передачи
фильтра-пробки от частоты по формуле (2.56).
Показана ширина полосы частот на уровне 0.7 для контура с добротностью QNEW = ρ / Ri = 10.
ρ >> R i >> r ,
160 Ом >> 16 Ом >> 0.1 Ома.
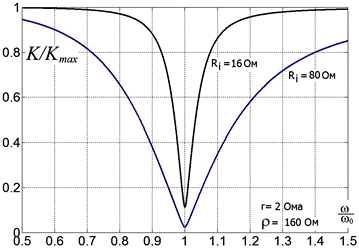
Рис. 2.30.
Те же зависимости для бόльшего сопротивления катушки индуктивности r = 2 Ома.
Пример: полосовой фильтр
В качестве другого примера рассмотрим полосовой фильтр (т.е. фильтр, хорошо пропускающий сигналы на частоте внутри заданной полосы и отсекающий сигналы других частот) – на рис. 2.31 приведена схема. Нетрудно видеть, что эта схема отличается от схемы на рис. 2.27 лишь тем, что выходное напряжение снимается с конденсатора (а не со всего контура). Опять примем, что выполнено неравенство ρ >>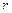 
. Записываем коэффициент передачи:
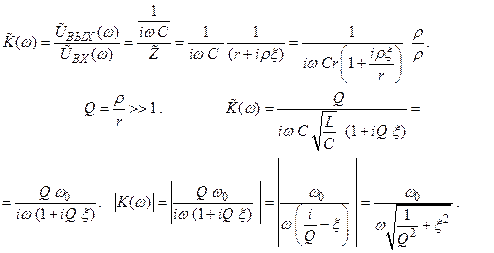
(2.59)
Выберем Тогда
(2.60)
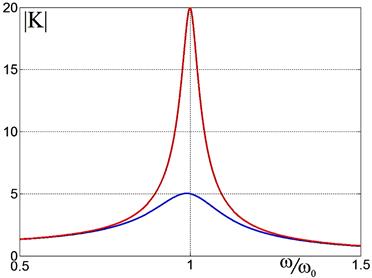
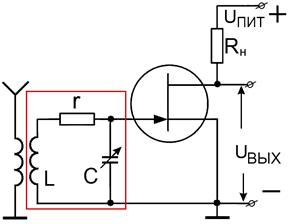
Рис. 2.31. Рис. 2.32.
Пример полосового фильтра в Резонансные кривые полосового фильтра
радиоприёмном устройстве. для двух значений добротности Q = 5 и 20.
На резонансе ( ω = ω 0 ) имеем: | K( ω 0)| = Q >> 1 .
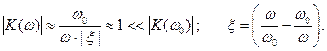
Вдали от резонанса: ω << ω 0 ,
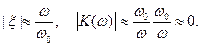
ω >> ω 0 ,
ширина полосы фильтра:
Это видно и на графике рис. 2.32.
Цепочка Вина
Цепочка Вина с равными сопротивлениями и ёмкостями (симметричная) попала в один раздел с LC-контурами потому, что частотная характеристика цепочки имеет максимум.
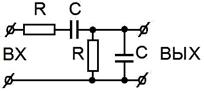
Рис. 2.33.
Схема цепочки Вина (Max Carl Wien).
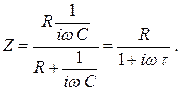
Импеданс параллельной RC цепочки будет: Здесь τ = RC.
Коэффициент передачи будет:
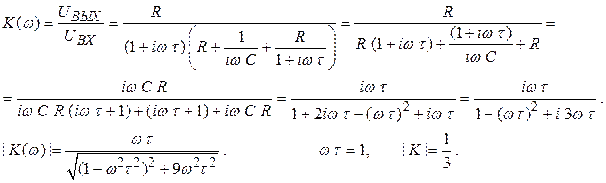
(2.61)
При (2.62)
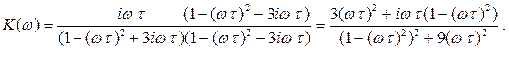Фазовую характеристику можно получить из (2.61), выделив вещественную и мнимую части.
(2.61')
Отсюда: (2.63)
Графики частотной характеристики приведены ниже. При ωτ = 1 ЧХ достигает максимума, и на этой частоте сдвиг фаз φ между входным и выходным напряжениями равен нулю.
Эти свойства используются в генераторах низкой частоты. Современная схема происходит из работы Уильяма Хьюлетта на степень магистра в 1939 г. в Стэнфордском университете. Хьюлетт с Дэвидом Паккардом основали фирму Хьюлетт-Паккард. Их первой продукцией был прецизионный синусоидальный генератор HP200A, основанный на мосте Вина.
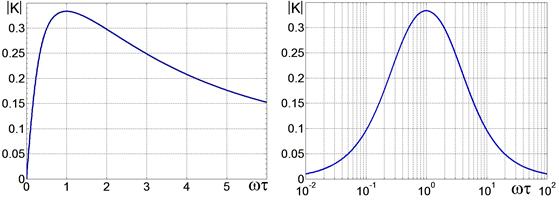
Рис. 2.34. Рис. 2.35.
ЧХ симметричной цепочки Вина с линейной и логарифмической шкалой частот.
Параллельный контур
Рассмотрим параллельный колебательный контур, возбуждаемый гармоническим генератором тока, то есть таким генератором, ток которого не зависит от сопротивления внешней цепи (рис. 2.36). Опять будем рассматривать только случай установившихся колебаний. Выражение для комплексной проводимости параллельного контура можно найти, если сложить проводимости индуктивности, ёмкости и сопротивления.
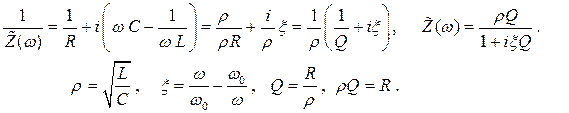
(2.64)
Здесь
Расстройку ξ мы ввели при выводе формулы (2.40), а добротность Q для данной схемы параллельного контура определена не так, как у последовательного.
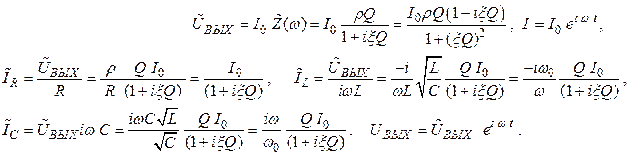Выходное напряжение: (2.65)
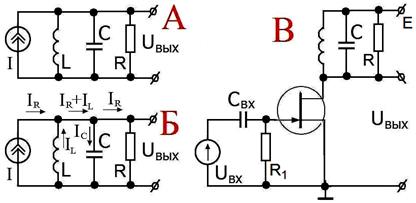Заметно, что IC = – IL при ω = ω0 или ξ = 0, ток от генератора течёт только через сопротивление R и токи через индуктивность и ёмкость в Q-раз больше. Токи равны и противофазны! При этом, конечно, сопротивление контура равно R и говорят, что оно чисто омическое.
Рис. 2.36.
А – параллельный колебательный контур.
Б – токи в цепи на резонансе.
В – пример использования параллельного контура в цепи стока резонансного усилителя на полевом транзисторе.
Частотная характеристика резонансного усилителя, показанного на схеме рис. 2.36 В, определяется частотной зависимостью модуля импеданса контура. Из (2.64) мы можем получить эту зависимость:
(2.66)
При ξ =0 модуль импеданса равен ρ Q = R.
На рис. 2.37 показан график зависимости обезразмеренного импеданса | Z ̃ / ρ| от частоты. Он имеет максимум на резонансной частоте, равный значению добротности Q.
Значение частот, при которых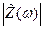 
равен 0.7 от максимального можно найти из (2.66).
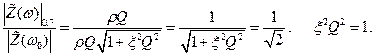
Такое уравнение мы уже решали
(см. (2.57), (2.58)).
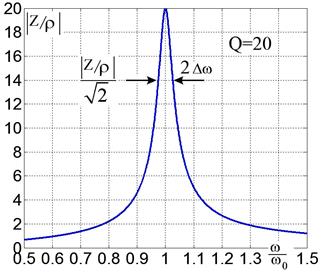
Рис. 2.37.
Зависимость безразмерного модуля импеданса параллельного контура от частоты.
На уровне 0.7 получаем условие ξ2 Q2 = 1.
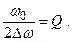
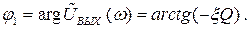Из (2.65):
Напряжение на выходе сдвинуто по фазе относительно тока генератора. Формула для фазы получается такая же, как и (2.45) а, значит, и график будет такой же. Поэтому, посмотрите график на рис. 2.23.
И векторная диаграмма токов на резонансе будет похожа на рис. 2.21. Токи в катушке индуктивности L и в конденсаторе C будут равны и противофазны! И вдвоём не будут потреблять энергию от источника питания, который будет работать только на нагрев резистора R.
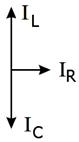
Рис. 2.38.
Векторная диаграмма токов на резонансе.
Для предельных случаев большой и малой добротностей получаем для уровня 0.7 ξ2 Q 2 =1.
Решая это биквадратное уравнение для Q << 1, нужно при извлечении корня опять удерживать и линейный и квадратичный члены разложения бинома Ньютона.
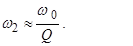
При Q << 1 ω1 ≈ Q ω 0 ,
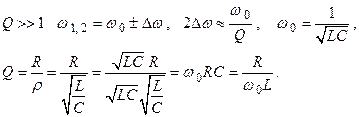
При
(2.67)
Заметим, что для нашего параллельного контура определение добротности Q отличается от определения добротности для последовательного контура.
В последовательном – чем меньше сопротивление, тем выше добротность. См. (2.40).
В параллельном – чем больше сопротивление, тем выше добротность. См. (2.67). Это вполне логично.
Добротность
Понятие добротности является важнейшей характеристикой резонаторов. Во многих приборах максимальная величина добротности является ключевым параметром.
Приведём различные определения добротности Q:
Запасённая энергия Это из (2.49).
( Потеря энергии за период )
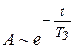Введём новую константу TЗ – время затухания в контуре, в котором амплитуда
свободных колебаний уменьшается по закону (см. (2.36)).
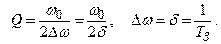
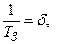
Тогда из (2.36) а из (2.41 и 2.55)
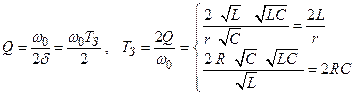
(последовательный контур),
(параллельный контур).
Свободные колебания в контуре затухают по закону e – δt . Если t = QT, то
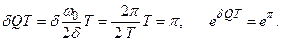
Итак, при свободных колебаниях амплитуда уменьшается в e π раз, то есть в 23 раза за
Q периодов. Посмотрите на колебания в контуре с добротностью Q = 5 на рис. 2.20. Пятый максимум как раз в 23 раза меньше первого. Проверьте! Это ещё один замечательный способ представить себе, что такое добротность.
Таблица. Примеры добротностей различных резонаторов.
| Вид резонатора | Добротность | Частотный диапазон |
| Обычный LC контур при комнатной температуре | Q ≈ 50…300 | f ≈105…108 Гц |
| СВЧ резонатор при комнатной температуре | Q ≈ 50…105 | f ≈ 10 9 …10 12 Гц |
| Сверхпроводящий СВЧ резонатор при гелиевой температуре ~ 4 K | Q ≈ 10 6 …10 10 | f ≈ 10 9 …10 12 Гц |
Мкостный датчик
Ёмкостный датчик является прибором для высокоточных измерений механических смещений. Принцип его работы следующий. Генератор гармонических колебаний настраивается на склон резонансной частоты контура, как показано на рис. 2.40. Тогда изменение расстояния d между пластинами конденсатора (которое и измеряется) на величину Δd приведёт к изменению собственной частоты контура, а, следовательно, к сдвигу резонансной кривой. Это в свою очередь приведёт к изменению напряжения UС на конденсаторе на величину ΔUC , которое и измеряется. Можно показать, что при определённых условиях связь между ΔUC и Δd имеет вид
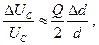
где Q — добротность контура. Чтобы оценить, какую величину Δd можно измерить, зададим следующие параметры:
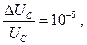
Q = 200, d = 0.1 мм. Тогда Δd =0.01 нм = 0.1 Å.
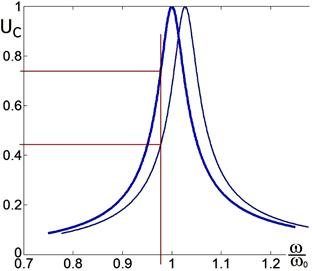
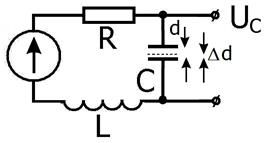
Рис. 2.39.
Схема простого ёмкостного датчика.
Настоящие схемы много сложнее.
Рис. 2.40.
При увеличении расстояния между пластинами конденсатора его ёмкость уменьшается. Резонансная кривая сдвигается в область бо́льших частот. Если частота генератора постоянна, то выходное напряжение в нашей ситуации падает.
Связанные контуры
Рассмотрим два связанных контура, изображённых на рис. 2.41. Пусть на вход первого действует гармоническое напряжение U BX (t)=U ̃0 eiωt и нас интересует, каково будет напряжение на выходе UВЫХ (t) = V ̃0 eiωt. Опять рассматриваем случай установившихся колебаний. Тогда для токов I1 и I2 в каждом контуре получаем систему двух уравнений:
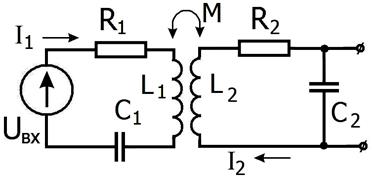
Рис. 2.41.
Схема двух связанных контуров.
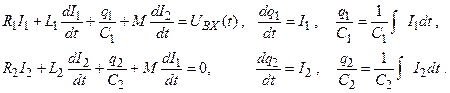
(2.68)
(2.69)
Здесь М – коэффициент взаимоиндукции.
Ищем токи в виде
где I ̃1 , I ̃2 – комплексные амплитуды. Подставляя их в систему (2.68, 2.69) получаем:
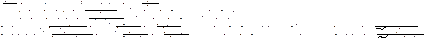
или
(2.70)
(2.71)
Эта система может быть решена. Для простоты рассмотрим более подробно простейший случай, когда контуры одинаковы:
Обозначим:
Заметьте, что здесь – безразмерное.
Тогда разделив оба уравнения (2.70, 2.71) на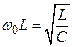 
, можно их переписать в виде:
Получим: (2.72)
(2.73)
Исключим Ĩ1 . В результате получим решение для Ĩ2 , через которое можно выразить комплексную амплитуду V ̃0 выходного напряжения и коэффициент передачи K ̃ :
Вычтем и получим:
Напряжение на конденсаторе будет (2.74)
(2.75)
(2.76)
Рассмотрим случай большой добротности, т.е.
При большой добротности нас будут интересовать только малые расстройки ξ << 1. Поэтому, мы можем считать, что κ ≈ const. Чтобы оценить форму резонансной кривой будем искать экстремумы квадрата модуля знаменателя (2.76) по переменной ξ :
(2.77)
Корни (2.77): (2.78)
Отсюда сразу видно, что при κ < δ NEW коэффициент передачи K ̃( ω) имеет один экстремум, а при κ > δ NEW — три экстремума. Два максимума и один минимум.
Рис. 2.42.
Резонансные кривые связанных контуров (2.76). QN = 100.
При увеличении связи между контурами резонансные кривые становятся двугорбыми.
Буквой П помечены кривые, более всего похожие на эту букву.
Использование комбинации нескольких контуров позволяет сделать почти идеальный
П-образный полосовой фильтр. Ширина полосы и крутизна фронтов зависит от числа и параметров использованных контуров.
Для любознательных. Не для экзамена.Программа для MATLAB . Вычисляет и строит кривые рис.2.42.
clear all; clc; % Рис.2.46. Связанные контура
FigureColor=[1,1,1]; hFigure=gcf; set(hFigure, 'Color', FigureColor)
for M =0.002: 0.002: 0.022 %Разные коэффициенты связи
del=.01; %Дельта
w=[0.96:.0001:1.04]; %Омега
kap=M./w; %Каппа
ksi=(w.*w-1)./w; %Кси
K=M./sqrt((kap.*kap+del.*del-ksi.*ksi).*(kap.*kap+del.*del-ksi.*ksi)+4.*del.*del.*ksi.*ksi);
%Модуль коэффициента передачи
plot(w+4*M,K-M*2500,'b-', 'LineWidth',3); hold on; %grid on;
end
Трансформатор
В электротехнике трансформатор (рис. 2.43) представляет собой устройство для увеличения или уменьшения переменного напряжения. В радиоэлектронике он ещё используется и для согласования нагрузок, а также для разделения цепей питания. Рассмотрим его работу подробнее. Опять записываем входное напряжение генератора синусоидального напряжения в комплексной форме UВХ ( t) = U 1 e iωt , а токи в каждом контуре в виде I1 = i1 e iωt , I2 = i2 e iωt . Тогда, записывая правило Кирхгофа в каждом контуре, получим систему:
(2.79)
(2.80)
Рис. 2.43.
Схема идеального трансформатора.
Здесь мы для дальнейшего удобства выбрали знак (–) перед коэффициентом взаимоиндукции М. Обычно в электротехнических приборах для работы трансформатора должны быть выполнены три условия:
1. Коэффициент взаимоиндукции М максимален, т.е. М 2 ≈ L1 L2.
2. Индуктивное сопротивление в первом контуре значительно больше активного, т.е. R1 << ω L1 .
3. То же самое для второго контура: R2 << ω L2 .
Используя эти условия, и вводя обозначение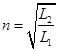 
, получаем из уравнения (2.80):
Величина n называется коэффициентом трансформации (это название понятно из последнего равенства). Индуктивность пропорциональна квадрату числа витков для идеального трансформатора с полностью общим магнитным потоком. Потерями магнитного потока пренебрегаем.
Отношение числа витков – это коэффициент трансформации: w2/ w1 = n. Если трансформатор повышает напряжение, то ток во вторичной обмотке уменьшается.
Решаем систему (2.79, 2.80), учитывая условия работы трансформатора.
Из (2.80)
(2.81)
(2.82)
(2.83)
Из выражений (2.82, 2.83) следует, что трансформатор на рис. 2.43 может быть представлен двумя эквивалентными схемами, изображёнными на рис. 2.44.
Можно сказать, что схема А “приведена к выходу” – она показывает, какой эквивалентный генератор действует во вторичной цепи с сопротивлением R2 .
Тогда схему Б можно назвать “приведённой ко входу” – по ней видно, как сопротивление R2 пересчитывается в эквивалентное сопротивление в первичной цепи генератора U1.
Рис. 2.44.
Две
эквивалентные
схемы
трансформатора.
Из (2.83) и схемы А мы можем рассчитать напряжение U2 = i2 R2 на нагрузке во вторичной цепи и вычислить коэффициент передачи напряжения K:
при (2.84)
Мы видим, что коэффициент передачи равен коэффициенту трансформации (K ~ n) лишь при достаточно малом сопротивлении в первичной цепи, т.е. при R2 >> n2 R1 , и полностью совпадает лишь при разомкнутой внешней цепи, то есть в режиме холостого хода.
В заключение выпишем выражения для мощности во вторичной цепи, соответствующие двум эквивалентным схемам:
– схема А , – схема Б . (2.85)
Они одинаковы. Мощность здесь поделена на 2 потому, что ток синусоидальный. А эффективное значение синусоидального тока равно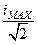 
.
Трансформаторы часто применяются для согласования источника сигнала с нагрузкой. Действительно, в простейшей схеме с источником напряжения, внутреннее сопротивление которого равно Ri , передаваемая в нагрузку мощность зависит от сопротивления нагрузки RH. Если сопротивление нагрузки равно нулю, то на ней нет напряжения и мощность тоже равна нулю. Если сопротивление нагрузки стремится к бесконечности, то ток стремится к нулю, а вместе с ним и мощность.
Где находится максимум передаваемой мощности?
Рис. 2.45.
Согласование с нагрузкой.
Максимум при
По схеме А: то есть . (2.86)
Запомните! Это – нужная формула!
Если то из
Это ток холостого хода, ХХ, в первичной обмотке.
Ток ХХ во вторичной обмотке будет: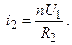 
Если то Это – ток короткого замыкания, КЗ.
И, наконец, , то есть сопротивление трансформируется пропорционально n2.
Максимальная мощность передаётся в нагрузку при равенстве внутреннего (выходного) сопротивления источника напряжения и сопротивления нагрузки. Коэффициент трансформации для согласования должен быть равен корню из отношения сопротивлений (2.86).
Рис. 2.46.
Простой делитель напряжения. Чтобы понизить его выходное сопротивление (R g), можно параллельно выходу подключить небольшое сопротивление R 2. Здесь удобно применить ещё один способ определения выходного сопротивления двухполюсника. Нужно только вычислить или измерить сопротивление (или импеданс) между выходными клеммами при закороченных источниках ЭДС (как на рис. 2.46) или при разомкнутых генераторах тока. Кстати, выходное сопротивление простого делителя напряжения по теореме об эквивалентном генераторе равно сопротивлению резисторов R 1 и R 2 , включённых параллельно.
3. Теория гармонических спектров сигналов
Сигналы
В радиотехнике важным понятием является сигнал – изменение физической величины, несущее информацию, кодированную определённым способом, либо синхронизированное отсутствие изменения физической величины. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым сообщением. Понятие "сигнал" позволяет абстрагироваться от конкретной физической величины, например тока, напряжения, давления в акустической волне и рассматривать вне физического контекста явления связанные с кодированием информации и извлечением её из сигналов, которые обычно искажены шумами. В исследованиях сигнал часто представляется функцией времени, параметры которой могут нести нужную информацию. Рассмотрим два примера.
Рис. 3.1.
Азбука Морзе. Буква "А".
Точка, пауза с длительностью точки, тире с длительностью в три точки. Паузы между буквами – три длительности точки, между словами – семь.
В 1957 г. в СССР был запущен первый в мире спутник. Он подавал сигналы, похожие на морзянку, но в длительности сигнала и паузы содержалась информация о давлении и температуре на борту.
Распространённым случаем является запись информации изменением параметров “синусоидальной” несущей. Можно записывать информацию, меняя амплитуду (АМ – амплитудно-модулированный сигнал), меняя частоту или фазу (ЧМ, ФМ – частотно- или фазово-модулированный сигнал). Если относительная величина модуляции мала (m << 1), то гармонические функции удобны для анализа. Удобным методом изучения свойств сигналов различной природы является Фурье-анализ.
Рис. 3.2.
Амплитудно-модулированный сигнал. "AM".
Рис. 3.3.
Амплитудно-модулированный
сигнал без несущей.
"DSB" (Double Sideband).
Рис. 3.4.
Сигнал несущей, промодулированной по частоте.
"FM" (Frequency Modulation).
Напряжение, модулирующее несущую.
Сигнал может иметь форму радиоимпульса (рис. 3.5А) или видеоимпульса (рис. 3.5Б). Можно сказать, что видеоимпульс – это огибающая радиоимпульса. А иногда говорят, что радиоимпульс – это видеоимпульс с высокочастотным заполнением. Заполнение не обязательно синусоидальное.
Рис. 3.5.
А – Радиоимпульс.
Б – Видеоимпульс.
Ряды Фурье
Если f( t) – "хорошая" периодическая функция с периодом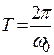 
, то её можно разложить в ряд Фурье.
(3.1)
(3.2)
Этот ряд можно записать и в другом виде:
Все необходимые тригонометрические формулы есть в приложении.
Окончательно: (3.3)
Где (3.4)
Аналогично:
(3.5)
Каждый отдельный член ряда (3.3) или (3.5) называется гармоникой. Часто гармоникой называют только амплитуду cn .
Из формулы Эйлера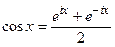 
.
Представляя каждый косинус в (3.5) суммой этих комплексно-сопряжённых слагаемых, получим:
(3.6)
Таким образом, разложение в ряд по косинусам можно заменить разложением по экспонентам, если ввести комплексные амплитуды гармоник:
(3.7)
(3.8)
Если договориться, что для отрицательных n мы будем вычислять то есть менять знак в (3.8) на минус не перед i, а перед n, то
(3.9)
Это разложение короче и симметричнее своего вещественного аналога и поэтому чаще применяется в физике.
Если в (3.1) косинус и синус записать по формулам Эйлера как
то получится:
Если сравнить это выражение с первой частью (3.8), то станет ясно, что комплексная амплитуда С̃ n связана с с n и ψ n , а также с а n и bn выражениями:
(3.10)
Сложим пару гармоник с номерами n и –n.
(3.11)
Получается, что сумма парных комплексных гармоник есть гармоника прежнего вещественного ряда Фурье.
Вещественная часть комплексного коэффициента С̃̃ n – чётная функция, а мнимая – нечётная по n.
(3.12)
чётная по n нечётная
Заметьте, что фаза есть нечётная функция относительно n, то есть относительно частоты (см. (3.4), (3.10) и (3.12)), а модуль комплексной амплитуды – чётная. Это и продемонстрировано на рис. 3.6. Действительно, видно, что в (3.10) мнимые части коэффициентов разного знака, а их модули одинаковые.
Иногда говорят, что ряд (3.9) при отрицательных n содержит гармоники с отрицательными частотами n ω0 . Это странно, но этот формализм можно объяснить тем простым фактом, что нам пришлось привлекать комплексно-сопряжённые амплитуды гармоник и знак минус появился не перед n , а перед i . С другой стороны, круговая частота ω – родственница угловой скорости. А угловая скорость вращения комплексного числа может быть и отрицательной.
n n
Рис. 3.6.
Пример комплексного спектра. По горизонтальной оси отложены номера гармоник.
Для объяснения смысла гармоник с отрицательными частотами обратимся к простейшему гармоническому колебанию и запишем его в виде двух разных выражений:
(3.13)
(3.14)
Первому выражению соответствует векторное представление, изображённое на рис. 3.7 А, а второму выражению – на рис. 3.7 Б.
Вещественная функция f( t) получается в первом случае как проекция вектора ,
равная А cos( ω 0 t – ψ), а во втором – как сумма проекций на ту же ось двух векторов (3.14) с
амплитудами , вращающимися с круговой частотой ω0 во взаимно противоположных
направлениях: – против часовой стрелки, – по часовой.
В сумме они дают ту же вещественную проекцию.
В соответствии с этим второе слагаемое в (3.14) можно трактовать как колебание с отрицательной в некотором смысле частотой. Видно, что в данном случае отрицательные частоты имеют формальный характер и связаны с применением комплексной формы для представления вещественной функции времени.
Рис. 3.7 А и Б. К объяснению смысла гармоник с отрицательными частотами.
P . S .
Дата: 2018-12-21, просмотров: 305.
