Сигнал проходит через линейную цепь без искажений, если форма его на выходе не меняется, но могут измениться только его величина и появиться запаздывание по времени. Это возможно только в случае равномерной частотной характеристики и линейной фазовой характеристики цепи.
Справедливость такого условия можно показать и аналитически с помощью преобразования Фурье. Пусть на вход цепи подано напряжение UBX ( t), имеющее спектральную функцию (или Фурье-образ) 
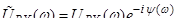. Выразим это напряжение с помощью интеграла Фурье:
Пусть цепь имеет коэффициент передачи с модулем K и с фазой, линейно растущей с частотой:
(3.52)
Тогда на выходе получим напряжение, определяемое выражением
или
Окончательно UВЫХ ( t) = K UВХ ( t – t0) . (3.53)
Действительно, напряжение на выходе имеет ту же форму, что и на входе, но изменено по величине в K раз и запаздывает по отношению к входному напряжению на время t0 . Для этого в (3.52) коэффициент передачи K должен быть постоянным, а фаза, как и написано в (3.52), должна линейно расти с частотой. Это нужно для того, чтобы гармоники с большей частотой запаздывали на большее число периодов.
Обычно передача сигнала (от "входа" к "выходу") может быть описана интегро-дифференциальным оператором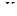 
:
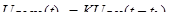
Переходя к преобразованию Фурье, можно записать это соотношение в виде:
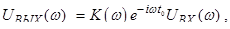
где K( ω) – комплексная рациональная функция (коэффициент передачи). Если K точно известно, то можно точно восстановить исходный сигнал, применив к полученному сигналу преобразование, обратное оператору .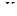
Часто удобнее (из-за технических ограничений) иметь дело не с самой функцией UВЫХ (t), а с рядом её дискретных отсчётов. Тогда естественно возникает вопрос, а эквивалентно ли представление функции в виде дискретных отсчётов самой функции? Здесь на помощь приходит теорема Котельникова. В зарубежной литературе она известна как теорема отсчётов – Sampling Theorem или теорема Найквиста – Nyquist- Shannon Theorem.
Теорема Котельникова (теорема отсчётов)
Зададим непрерывный сигнал U( t) набором отсчётов: U n = U( n Δ), где Δ — интервал дискретизации, 1/Δ — частота дискретизации (см. рис. 3.32).
Рис. 3.32. График функции U( t) и набор дискретных отсчётов Un c интервалом дискретизации Δ.
Это – наивысшая гармоника или наивысшая частота сплошного спектра сигнала.
Тогда справедлива теорема Котельникова (приводится без доказательства):
Если спектр сигнала ограничен и верхняя частота спектра меньше
то по дискретному набору Un можно точно восстановить исходный сигнал:
(3.54)
f c – частота Найквиста. Подчеркнём, что размерность f c – Гц.
В физическом эксперименте спектр любой функции всегда ограничен. Однако для математика функция, ограниченная по времени интервалом Т, имеет бесконечный спектр. В качестве примера можно привести формально неограниченный спектр прямоугольного сигнала, рассмотренный выше (см. рис. 3.11). На практике можно выбрать наивысшую частоту спектра fc так, чтобы “хвосты” спектра (содержащие частоты выше fс) содержали достаточно малую долю энергии сигнала. Величина малости определяется в каждом случае желаемой точностью воспроизведения сигнала.
Смысл теоремы в том, что наивысшая гармоника или наивысшая частота сплошного спектра сигнала должна быть задана двумя отсчётами.
Диоды
С точки зрения проводимости твёрдые вещества делятся на три категории: металлы, диэлектрики и полупроводники.
1. В металле есть свободные электроны, и поэтому их сопротивление мало.
2. В диэлектрике свободных электронов нет, все электроны распределены по атомам. Энергия отрыва (ионизации) электрона от атома велика. Естественным масштабом для оценки величины энергии ионизации является тепловая энергия, приходящаяся на колебательную степень свободы при T = 290K; kТ ~ 4·10–21 Дж = 0,03 эВ (k – постоянная Больцмана). Например, для алмаза энергия ионизации ε АЛМАЗ ~ 5,4 эВ >> kТ.
3. В беспримесном полупроводнике электроны тоже распределены по атомам, но энергия ионизации меньше, например, для кремния Si εSi ~1,1 эВ, для галлия εGa ~ 0,67 эВ. Поскольку энергия отрыва электрона от атома всё-таки значительно больше kТ, то сопротивление беспримесных полупроводников тоже довольно значительно.
4. Несобственный полупроводник – это полупроводник, легированный примесями, атомы которых легко “расстаются” с электронами или присоединяют их. Различают n-тип (например, донор мышьяк As в Si) и р-тип (например, акцептор индий In в Si). Концентрация примесей обычно лежит в пределах ~ 1014 ... 1017 см-3. В 1 см3 Si порядка 0.5 1023 атомов. Энергия отрыва (или присоединения) мала, например, ε As ~ 0,01 ... 0,04 эВ ~ kТ.
n p
Рис. 4.1.
Кремний Si, легированный пятивалентным Или трёхвалентным индием In
мышьяком As (проводимость n-типа). (проводимость p-типа).
В данном случае перенос заряда В данном случае перенос заряда
осуществляется электронами. осуществляется дырками.
От количества свободных носителей и их подвижности зависит проводимость вещества. В чистых полупроводниковых веществах количество свободных носителей малó. Это и определяет низкую проводимость (или высокое удельное сопротивление) чистых полупроводников. При наличии примесей удельная проводимость может сильно изменяться. Например, у чистого германия проводимость около 2 Ом-1 м-1. При введении в германий всего 10-5 примеси мышьяка, удельная проводимость увеличивается до 2·104 Ом-1 м-1.
На использовании несобственных (легированных) полупроводников основана большая часть современной электроники. Простейший прибор из этого класса – полупроводниковый диод, с которого мы и начнём рассмотрение.
Полупроводниковый диод
В основе большинства полупроводниковых диодов и транзисторов лежит контакт двух полупроводников с различным типом электропроводности. Такой контакт называют электронно-дырочным переходом или p- n-переходом. Он может быть получен, например, путём диффузии донорной примеси в полупроводник p-типа.
В зоне контакта электроны из n полупроводника диффундируют в область p полупроводника. Встречая на своём пути дырки, электроны рекомбинируют с ними и выходят из игры. Этот процесс поддерживается постоянно, и таким образом реализуется состояние динамического равновесия: в приграничном слое в р полупроводнике постоянно присутствует слой отрицательного заряда. Аналогично положительно заряженные дырки из р полупроводника диффундируют в приграничный слой n полупроводника, в котором возникает слой положительного заряда (см. рис. 4.2a). Эти поверхностные заряды образуют систему, подобную плоскому конденсатору так, что распределение потенциала имеет вид ступеньки (рис. 4.2а).
Рис. 4.2. Схема действия полупроводникового диода.
Прямое напряжение
(UД > 0) – малое сопротивление.
Обратное напряжение
(UД < 0) – большое сопротивление.
Говорят, что возникает контактная разность потенциалов. Ток неосновных носителей при этом практически ничтожен, так как он лимитируется малым числом неосновных носителей.
Теперь рассмотрим, что будет, если к р полупроводнику приложить положительное напряжение, а к n полупроводнику – отрицательное, как показано на рис. 4.2б. В этом случае возникает ток, причём положительные дырки движутся слева направо, а отрицательные электроны справа налево. В области контакта эти потоки встречаются и рекомбинируют. За счёт этого притока темп рекомбинации в области контакта становится больше, чем в случае отсутствия тока через контакт. Увеличение рекомбинации в контакте приводит к тому, что объёмные заряды в области контакта уменьшаются, следовательно, уменьшается и контактная разность потенциалов. Это в свою очередь уменьшает сопротивление контакта. Таким образом, при такой полярности напряжения ток нелинейно возрастает при увеличении напряжения. Такой режим диода называют работой в прямом направлении. В прямом направлении сопротивление диода нелинейно уменьшается с увеличением напряжения.
Рассмотрим, что будет, если приложить напряжение обратной полярности, как показано на рис. 4.2в. В этом случае возникает такой ток, что положительные дырки двигаются справа налево, а отрицательные электроны – слева направо. При этом основные носители – и электроны, и дырки – движутся прочь от области контакта. В результате процессы рекомбинации в области контакта замедляются. Это приводит к увеличению объёмных зарядов вблизи контакта, а, следовательно, и к увеличению контактной разности потенциалов. В свою очередь это значительно увеличивает сопротивление контакта. Такой режим диода называют работой в обратном направлении. В обратном направлении сопротивление диода велико, и ток практически отсутствует.
Если продолжать увеличение напряжения обратной полярности, то при некотором напряжении произойдёт пробой перехода. Это связано с тем, что в закрытом состоянии перехода почти всё приложенное напряжение действует в тонком пограничном слое. Поэтому в нём формируется большая напряжённость электрического поля, способная ускорить электрон на малом расстоянии до энергий, достаточных для "выбивания" электрона из ковалентной связи. Далее уже оба электрона будут ускорены, они выбьют ещё электроны и так далее. Получится подобие электронной лавины, приводящей к пробою перехода.
Можно дать и простое, наглядное объяснение таких сильных отличий проводимости перехода в разных направлениях. При включении перехода в прямом направлении (рис. 4.2б) дырки в левой области будут двигаться к границе раздела, и электроны из правой области также будут двигаться к границе раздела. На границе они будут рекомбинировать. Ток на всех участках цепи обеспечивается основными носителями, сам переход обогащён носителями тока. Проводимость перехода будет большой.
При включении перехода в обратном направлении и дырки в левой области будут двигаться от границы раздела, и электроны из правой области также будут двигаться от границы раздела. На границе раздела областей, в итоге, не останется основных носителей тока. Ток на этой границе обеспечивается очень малым числом неосновных носителей, образовавшихся вблизи тонкого перехода. Проводимость перехода будет малой.
Таким образом, р- n переход хорошо проводит ток в прямом направлении и практически не проводит ток в обратном направлении. Такие полупроводниковые диоды широко применяются в электронике. На рис. 4.3 изображена типичная вольт-амперная характеристика (ВАХ) диода. Типичные величины прямого напряжения порядка UПРЯМ ~ 0.5 В.
Из сказанного выше ясно также, что диод в закрытом состоянии обладает ёмкостью. Характерная нелинейная зависимость ёмкости от обратного напряжения на диоде приведена на рис. 4.5. Ёмкость С перехода зависит от площади S контакта, типичная величина – C/ S ~ 103 пФ/см2. Комбинация сопротивления контакта и ёмкости определяет его быстродействие в радиотехнических устройствах, которое обычно измеряют величиной предельной частоты, вплоть до которой используется данный диод. Типичная частота для точечного p- n-перехода f = ( RC)–1 ~ 1012 Гц, для плоскостного p- n-перехода f = ( RC)–1 ~ 109 Гц.
Рис. 4.3. Рис. 4.4.
Вот как выглядит вольт-амперная Та же характеристика, но масштаб
характеристика силового для обратного тока увеличен в 1000 раз.
кремниевого диода Д233. Обратите внимание! Во многих
учебниках ВАХ диода рисуют как на
этом рисунке, а про смену масштаба
пишут очень маленькими буквами!
Рис. 4.5.
Зависимость ёмкости диода (варикапа) BB201 от обратного напряжения.
Рис. 4.6. Здесь изображена прямая часть Рис. 4.7. Это прямая часть вольт-амперной
вольт-амперной характеристики точечного характеристики силового
германиевого диода Д2Е. Она хорошо кремниевого диода Д233.
описывается квадратичной зависимостью.
Заметьте, что при напряжениях в несколько десятых вольта сопротивления диодов очень большое, и ток в прямом направлении через него практически не идёт. А при напряжении
больше 0.5 В дифференциальное сопротивление порядка единиц Ом. Это свойство
используется в ограничителях входного напряжения.
Рис. 4.8.
Аналогично выглядит и характеристика высокочастотного кремниевого диода КД521А. Касательная к характеристике в выбранной точке даёт дифференциальное сопротивление около 7 Ом.
ВАХ кремниевого диода сильно отличается от германиевого и уже нельзя говорить о квадратичной зависимости. Сплошная кривая i ~ U4 .
Зависимость обратного тока от напряжения у всех диодов выглядит примерно одинаково. Обратный ток очень мал и он растёт с ростом напряжения.
Дата: 2018-12-21, просмотров: 269.
