Давайте рассмотрим, при каких условиях цепочки, изображённые на рис. 2.14, будут приближённо дифференцирующими для гармонического (синусоидального) сигнала.
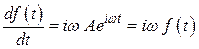
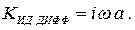 Из (2.10) . Значит, коэффициент передачи идеальной
Из (2.10) . Значит, коэффициент передачи идеальной
дифференцирующей цепочки должен быть (2.23)
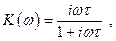
Коэффициент передачи этих цепочек будет: (2.24)
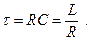
где постоянные времени этих цепочек:
 Из (2.24) виден ещё один признак хорошего дифференцирования: ωτ должно быть много меньше единицы, а постоянная времени цепочки должна быть много меньше периода
Из (2.24) виден ещё один признак хорошего дифференцирования: ωτ должно быть много меньше единицы, а постоянная времени цепочки должна быть много меньше периода
синусоиды T: то есть частота (2.25)
При этом условии в знаменателе (2.24) останется только единица, а коэффициент передачи будет |K( ω)| << 1.
Обратим сразу внимание, что две цепочки, составленные из разных элементов, обладают подобными характеристиками. Более того, эти цепочки становятся идентичными при RC = L/ R.
Это означает, что на выходе наших цепочек мы получим производную от входного сигнала, если частоты будут достаточно низкими, ω << 1/τ . Естественно, мы получим производную в некотором приближении, и это приближение будет тем лучше, чем лучше выполняется неравенство (2.25).
Условие дифференцируемости на временно́м языке
 Кроме частотного рассмотрения, полезно рассмотреть действие наших дифференцирующих цепочек на временно́м языке.
Кроме частотного рассмотрения, полезно рассмотреть действие наших дифференцирующих цепочек на временно́м языке.
Рис. 2.15.
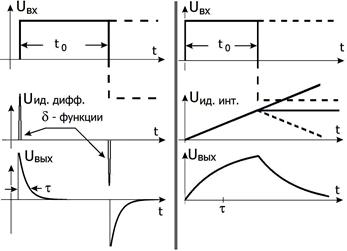
Слева – дифференцирование прямоугольного импульса.
Справа – интегрирование прямоугольного импульса.
В качестве примера рассмотрим прямоугольный импульс длительности t0 , изображённый на рис. 2.15 слева. Прямоугольный импульс можно представить как суперпозицию (наложение) двух ступенек (показаны пунктиром на верхнем графике рис. 2.15).
Сразу отметим, что математически производная от такого прямоугольного импульса с вертикальными фронтами есть две дельта-функции ( UИД ДИФФ на рис. 2.15 слева). Это следует из того, что производная от ступеньки (функции Хевисайда) есть просто дельта-функция.
Нетрудно найти выходное напряжение в наших цепочках, воспользовавшись переходной характеристикой (2.21) – это будут две спадающие экспоненты, как показано на рис. 2.15 слева внизу.
Причём, если постоянная времени τ << t0 , (2.26)
то выходное напряжение похоже на производную от сигнала.
Таким образом, мы получили приближённое условие дифференцируемости на временном языке. Это условие приложимо и к сигналу произвольной формы, если под t0 мы будем понимать характерную длительность сигнала.
Заметим, что условия (2.23) и (2.26) эквивалентны, а применение одного или другого зависит от того, какой язык (частотный или временно́й) используется в задаче.
Интегрирующие цепочки
Рассмотрим для примера две интегрирующие цепочки, изображённые на рис. 2.16.
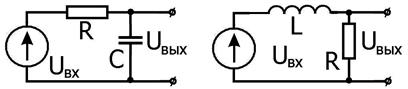
Рис. 2.16.
RC и RL-цепочки.
Эти цепочки имеют идентичные характеристики при RC = L/ R:
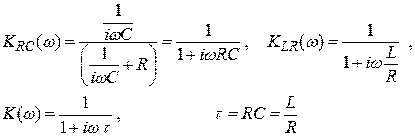
(2.27)
где – это время релаксации цепочки.
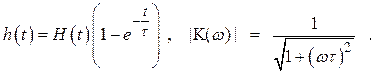
h ИНТ (t)= 1 – h ДИФФ (t), (2.28)
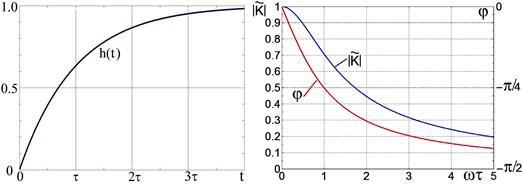 Рис. 2.17. Переходная, частотная и фазовая характеристики интегрирующей цепочки.
Рис. 2.17. Переходная, частотная и фазовая характеристики интегрирующей цепочки.
Дата: 2018-12-21, просмотров: 372.