Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Поверхностный слой очень тонок, поэтому поверхностную энергию можно считать постоянной величиной по всей толщине слоя.

В открытых системах изменение этой энергия может быть связано с превращением ее в энергию Гиббса, в теплоту, в химическую энергию, в электрическую энергию и. т. д.

С точки зрения термодинамики, это можно представить следующим образом.

Объединенное уравнение первого и второго закона термодинамики для открытых гетерогенных систем, в которых протекает химическая реакция, изменение поверхности (П) и совершается электрическая работа (φ – электрический потенциал, q – количество электричества) имеет вид:

 

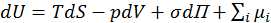d 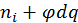(1.1.1)

 

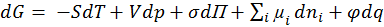(1.1.2),

 

где 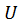 - внутренняя энергия;  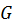- энергия Гиббса; 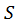– энтропия;  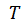– температура; 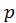– давление; 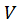– объем;  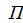- площадь поверхности;  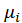- химический потенциал;  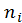- число моль.

В этих уравнениях σ – это поверхностное натяжение, которое математически можно представить как частную производную любого термодинамического потенциала по площади межфазной поверхности при постоянстве других параметров:

 

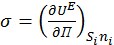                              (1.1.3)

 

Из этого следует, что изменение поверхностной энергии можно рассматривать как произведение σ d П .

Для термодинамического описания поверхности раздела фаз используют два подхода:

• Метод «слоя конечной толщины»;

• Метод избыточных величин Гиббса.

Суть первого подхода состоит в том, что в системе жидкость - газ межфазовая граница характеризуется наличием поверхностного слоя конечной толщины в несколько диаметров молекул. Поверхностный слой состоит из двух слоев. Один из них толщиной 1 – со стороны фазы 1, а второй - 2 - со стороны фазы 2 (рис 1.2).

 

 

Рис. 1.2. Сравнение термодинамических методов: I – метод «слоя конечной толщины»; II – метод избыточных величин Гиббса

 

Поверхностный слой по строению неоднороден, для него характерно резкое отличие термодинамических параметров (плотность, концентрации компонентов, давление) от значений тех же параметров в объемной фазе. Этот слой – открытая термодинамическая система (то есть может происходить обмен энергией и массой). Проблема состоит в том, что определить точно размеры поверхностного слоя затруднительно.

Метод избыточных величин Гиббса относит все изменения термодинамических параметров в поверхностном слое, по сравнению со значениями этих параметров в объемной фазе, к разделяющей поверхности, не имеющей толщины. Эта поверхность находится внутри поверхностного слоя и воспроизводит его форму. Реальную межфазовую поверхность Гиббс заменил на идеализированную поверхность нулевой толщины, назвав ее разделяющей поверхностью. Поверхностный слой обладает избыточной энергией (рис.1.2).

Выведем основное уравнение для межфазной поверхностной энергии.

Если система состоит из двух объемных фаз и поверностного слоя между ними, то условием равновесия любой изолированной системы при постоянных значениях общей энтропии, общего объема и общего количества каждого из компонентов является минимум ее внутренней энергии:

 

d(U¹ +U²+U) = dU¹+ dU² + dU = 0,  (1.1.4)

где dU ¹ , dU ² – изменение внутренней энергии объемных фаз 1 и 2; dU – изменение внутренней энергии поверхностного слоя.

Изменение внутренней энергии для каждой фазы из объединенного уравнения первого и второго законов термодинамики имеет вид:

 

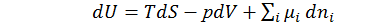(1.1.5)

 

При условии равенства изменения объемов фаз общим условием термического и химического равновесия в системе будет:

 

Т¹ = Т² = Т

 

μ_i¹ = μ_i² =μ_i

 

При рассмотрении термодинамических характеристик поверхностного слоя учитывают, что поверхностный слой обладает избыточными величинами внутренней энергии, энтропии, чисел моль компонентов:

 

U^E = U – U¹ – U²;

 

S^E = S – S¹ – S²;

 

n_i^E= n_i – n_i¹ – n_i²,

 

где U^E – полная поверхностная энергия;S^E – поверхностная энтропия слоя; n_i^E – избытки каждого из компонентов в поверхностном слое.

 

Тогда

 

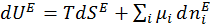.        (1.1.6)

 

Если межфазная поверхность раздела изменяется, то выражение приобретает вид:

 

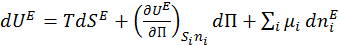, (1.1.7)

где 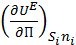 - поверхностное натяжение .

 

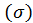Поверхностная энергия является однородной функцией. Таким образом, в соответствии с правилами интегрирования однородных функций, выражение (1.1.7) принимает вид:

 

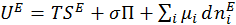      (1.1.8)

 

После полного дифференцирования и сопоставления с уравнением (1.1.6) получаем:

 

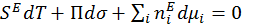           (1.1.9)

 

 

При постоянной температуре:

 

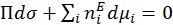                       (1.1.10)

 

Уравнения (1.1.8), (1.1.9) и (1.1.10) носят название фундаментальных уравнений Гиббса для межфазного поверхностного слоя.

Из вышесказанного следует:

¢ На границе раздела фаз располагается переходнаязона – поверхностный слой, свойства которого отличаются от свойств объемных фаз.

¢ В поверхностных явлениях участвуют молекулы, которые находятся у самой поверхности тел.

¢ Если размеры тел достаточно велики, то число таких молекул весьма мало по сравнению с числом молекул в основном объеме. В этом случае поверхностные явления обычно не играют большой роли.

¢ Однако для тел малых размеров поверхностные явления приобретают огромное значение.

¢ Свойства молекул на границе раздела фаз и в объеме отличаются в связи с изменением ближнего порядка и силового поля на поверхности и в объеме.

¢ Это приводит к тому, что удельные значения экстенсивных параметров: объема, энтропии, энергии, теплоемкости, химического состава и ряда других величин, – в общем случае окажутся различными для объема и поверхностного слоя каждой фазы.

¢ К поверхностным явлениям относят все эффекты, связанные с различием термодинамических свойств изучаемых систем, зависящих от различного поведения молекул в поверхностном слое и объеме фазы.

 

 

Поверхностное натяжение

Уже упоминалось, что поверхностное натяжение - это частная производная любого термодинамического потенциала по площади межфазной поверхности при постоянстве соответствующих параметров (1.1.3).

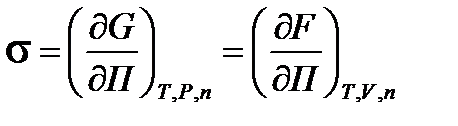
                                                                      (1.2.1.)

Таким образом, получается, что поверхностное натяжение (σ) - это мера поверхностной энергии. Оно характеризует избыток поверхностной энергии, приходящийся на 1 м²  межфазной поверхности.

По системе СИ, единицей измерения поверхностного натяжения является Дж/м²  или (Н·м)/м², то есть Н/м.

 Поверхностное натяжение является важнейшей термодинамической характеристикой поверхностного слоя. Физический смысл может иметь разное толкование. Поверхностное натяжение жидкости на границе с газом - это работа переноса молекул жидкости из объема на поверхность. Можно дать и другое определение поверхностному натяжению - это сила, действующую на единицу длины граничной поверхности.

Поверхностное натяжение зависит от температуры . Для чистых однокомпонентных систем на границе с газом оно понижается с повышением температуры, то есть 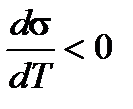, причем температурный коэффициент  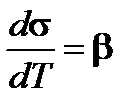имеет почти всегда отрицательное значение вплоть до температур, близких к критической:

 

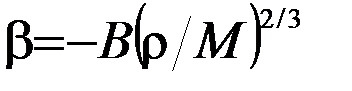,                  (1.2.2)

 

где В – коэффициент, постоянный для всех жидкостей; 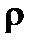 − плотность жидкости; М – молярная масса.

Уменьшение поверхностного натяжения с ростом температуры происходит из-за увеличения энтропии поверхностного слоя чистой жидкости по сравнению с энтропией внутри жидкости. Для расчета используют уравнение Гиббса – Гельмгольца для единицы поверхности:

 

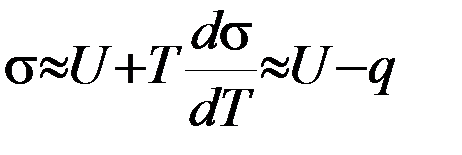,         (1.2.3)

 

где U – внутренняя энергия единицы поверхности, а q – связанная энергия единицы поверхности.

При линейном изменении поверхностного натяжения с температурой Т внутренняя энергия поверхностного слоя является температурным инвариантом, то есть не зависит от температуры. Это происходит потому, что при увеличении температуры свободная поверхностная энергия уменьшается на величину 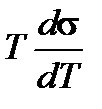, а связанная энергия на ту же величину возрастает.

При критической температуре исчезает различие между граничащими фазами, и поверхностное натяжение становится равным нулю. Для большинства неполярных жидкостей температурная зависимость поверхностного натяжения линейная и в первом приближении может быть представлена соотношением:

 

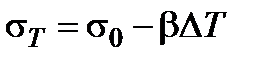,                    (1.2.4)

 

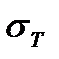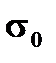где  и  − поверхностное натяжение при температуре Т и стандартной температуре;  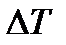− разность между данной и стандартной температурами;  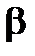– постоянная, равная температурному коэффициенту поверхностного натяжения, взятому с обратным знаком.

Другие вещества в меньшей степени соответствуют зависимости (1.2.4), но часто при проведении исследований этими отклонениями можно пренебречь.

В двухкомпонентных системах изменение поверхностного натяжения зависит от второго компонента. Вещества, уменьшающие σ, называются поверхностно-активными веществами (ПАВ). К ним относятся спирты, альдегиды, органические кислоты и их соли, амины и другие соединения. Особенностью строения их молекул является дифильность, то есть двойственность, характеризующаяся наличием неполярного (углеводородного) радикала и полярных групп −ОН; −СОН; −СООН; −NH₂ и др. (рис.1.3).

 

 

Рис.1.3. Схема ПАВ

 

Вещества, увеличивающие σ, называются поверхностно-инактивными веществами (ПИВ). К ним относятся электролиты.

Зависимость поверхностного натяжения от концентрации 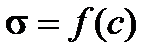при постоянной температуре называется изотермой поверхностного натяжения (рис.1.4).

 

 

 

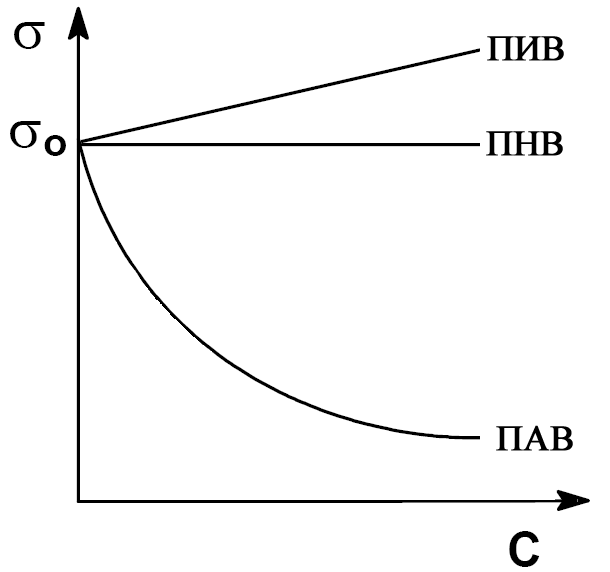
Рис.1.4. Изотермы поверхностного натяжения

 

Производная 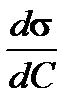называется поверхностной активностью и определяется из графика как тангенс угла наклона касательной с положительным направлением оси абсциссα, то есть как тангенс смежного угла 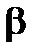, но с противоположным знаком (см. рис.1.5).

 

 

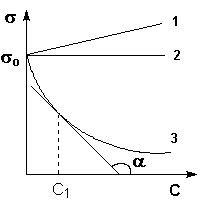
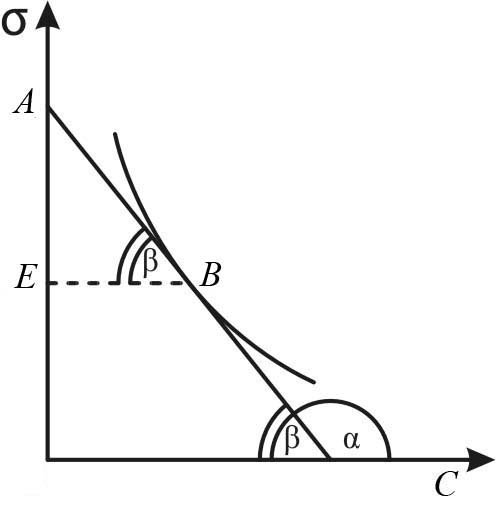
Рис.1.5. Графическое определение поверхностной активности

 

Поверхностная активность вещества, или его способность понижать поверхностное натяжение, увеличивается при переходе к каждому высшему гомологу в среднем в 3,5 раза. Эта зависимость была установлена и сформулирована как эмпирическое правило Дюкло - Траубе. Чем длиннее углеводородная цепь, тем меньшее сродство с водой имеют молекулы, и тем сильнее они стремятся собраться на границе раздела фаз, образуя насыщенный слой даже при самых маленьких концентрациях ПАВ в растворе.