Определение. Комплексными числами называются числа вида a + bi, где a и b – действительные числа, а число i, определяемое равенством i 2 = -1, называется мнимой единицей, если для этих чисел понятия равенства и действия сложения и умножения определены следующим образом:
1) два комплексных числа a 1 + b 1 i и a 2 + b 2 i называются равными, если
a 1 = a 2 и b 1 = b 2;
2) суммой двух комплексных чисел a 1 + b 1 i и a 2 + b 2 i называется комплексное число ( a 1 + a 2 ) +( b 1 + b 2 ) i;
3) произведением двух комплексных чисел a 1 + b 1 i и a 2 + b 2 i называется комплексное число ( a 1 a 2 - b 1 b 2 ) + ( a 1 b 2 + a 2 b 1 ) i.
4) вычитание : (a1 + b1i) – (a2 + b2i) = (a1 - a2) + (b1 = b2)i
5) деление: 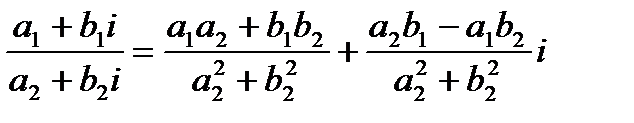
Модулем комплексного числа z = а + bi называется число 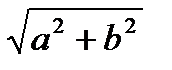 :
:
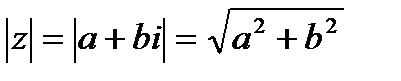 ,
, 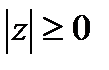 .
.
Аргумент комплексного числа z = а + bi записывается так φ =argz или φ =arg(а + bi). Наименьшее по абсолютной величине значение аргумента из промежутка 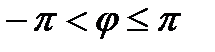 называется главным значением аргумента.
называется главным значением аргумента.
Если φ =arg(а + bi), то cos φ = 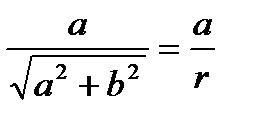 , sin φ =
, sin φ = 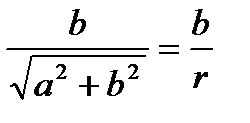 .
.
Практическая работа №7
Тема: Выполнение действий над комплексными числами
Цель работы: Формирование навыков при выполнении действий над комплексными числам, заданными в алгебраической форме
Задания.
1. Построить на плоскости точки, изображающие следующие комплексные числа:
1.1. а) 3 + 2i, б) 5, в) -4i
1.2. а) 2 + 4i, б) -3, в) 4i
1.3. а) -1 + 2i, б) 6i, в) 4.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел:
2.1. 9 + 2ix + 4iy = 10i + 5x - 6y
2.2. 2ix + 3iy + 17 = 3x + 2y - 18i
2.3. 5x – 2y + (x + y)i = 4 + 5i .
3. Найти модуль и главное значение аргумента комплексного числа:
3.1. -2 - 2i
3.2. 1 + i 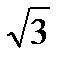
3.3. - 3i .
4. Выполнить действия:
4.1. а) 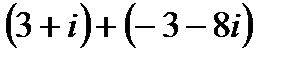
б) 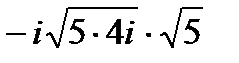
в) 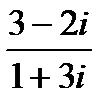
4.2 а) 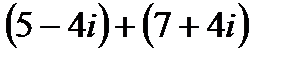
б) 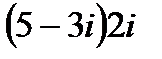
в) 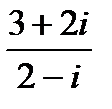
4.3 а) 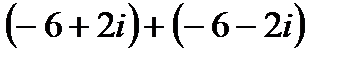
б) 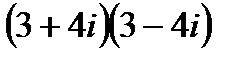
в) 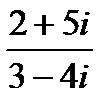
Тема « Основы дискретной математики»
Краткие теоретические сведения
Под множеством в математике понимают совокупность или собрание некоторых объектов. Сами объекты, входящие в данное множество, называются элементами этого множества.
Операции над множествами.
1. Пересечением множеств А и В называется множество тех и только тех элементов, которые принадлежат и множеству А и множеству В.
Пересечение множеств обозначается символом 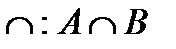 .
.
2. Объединением множеств А и В называется множество тех и только тех элементов, которые входят хотя бы в одно из множеств А и В.
Объединение множеств обозначается символом 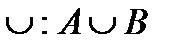 .
.
3. Разностью двух множеств А и В называется множество, состоящее из тех и только тех элементов множества А, которые не принадлежат множеству В.
Разность множеств Аи В обозначается символом \: А \ В.
Практическая работа № 8
Тема: Операции над множествами
Цель работы: Формирование навыков задания множеств различными способами, выполнение действий над множествами
Задания.
1. Составить список элементов множества, заданного следующим образом:
1.1 а) 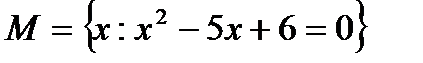 ; б)
; б) 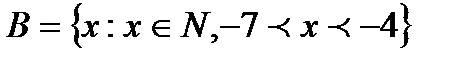 .
.
1.2 а) 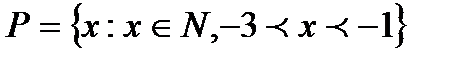 ; б)
; б) 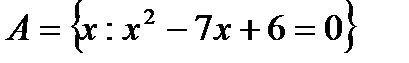 .
.
1.3 а) 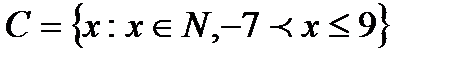 ; б)
; б) 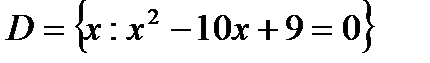 .
.
2. Найти объединение и пересечение множеств:
2.1 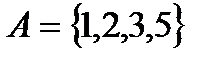 и
и 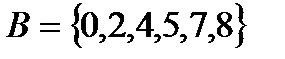 .
.
2.2 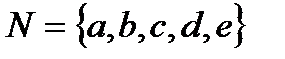 и
и 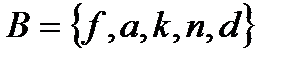 .
.
2.3 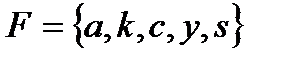 и
и 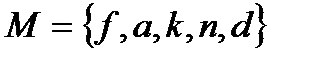 .
.
3. Выписав все подмножества заданного множества, подсчитайте их число:
3.1 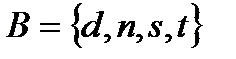 . 3.2
. 3.2 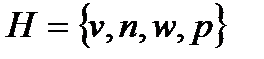 . 3.3
. 3.3 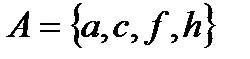 .
.
4. Выполните операции с заданными множествами:
4.1 а) 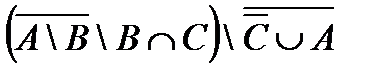 ; б)
; б) 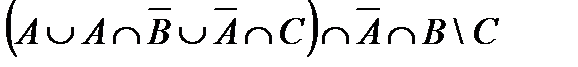 , где
, где 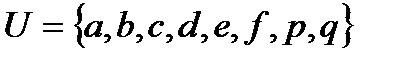 ,
, 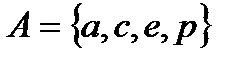 ,
, 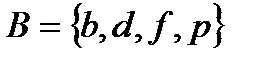 ,
, 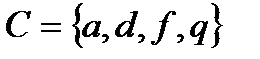 .
.
4.2 а) 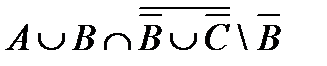 ; б)
; б) 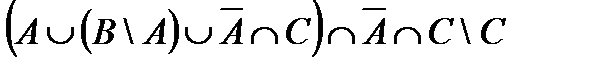 , где
, где 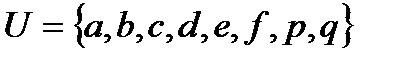 ,
, 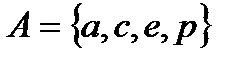 ,
, 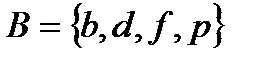 ,
, 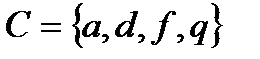 .
.
4.3 а) 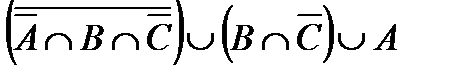 ; б)
; б) 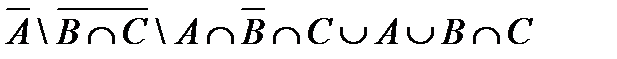 , где
, где 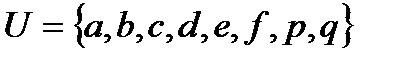 ,
, 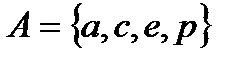 ,
, 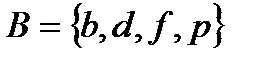 ,
, 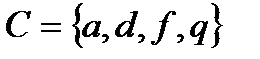 .
.
5. С помощью диаграмм Эйлера-Венна упростите выражение:
5.1 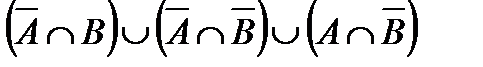 .
.
5.2 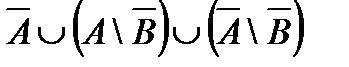 .
.
5.3 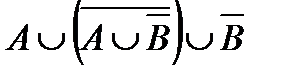 .
.
Примечание: Сначала выполняется операция дополнения (  ), затем пересечения
), затем пересечения 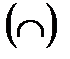 и только затем объединения
и только затем объединения 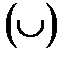 и разности
и разности 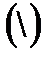 . Для изменения этого порядка в выражении используются скобки.
. Для изменения этого порядка в выражении используются скобки.
Контрольная самостоятельная работа
1. Найти решение системы линейных уравнений 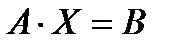 , пользуясь правилом Крамера.
, пользуясь правилом Крамера.
Варианты заданий
| Номер варианта | Матрица А коэффициентов системы | Столбец В свободных членов | ||
| 1 | 1 3 2 | 2 1 -1 | 1 4 1 | 3 5 -1 |
| 2 | 2 3 2 | -3 1 3 | 4 -2 -2 | 1 -1 1 |
| 3 | 5 6 2 | -2 4 -1 | 5 -2 4 | 3 2 3 |
| 4 | 2 3 5 | -1 7 4 | 6 -3 -5 | 1 10 9 |
| 5 | 3 5 3 | -2 -6 2 | 5 2 -3 | 6 1 2 |
| 6 | 2 3 1 | 5 -2 -2 | -3 2 4 | 4 3 3 |
| 7 | 1 2 3 | 3 -1 2 | -1 5 -2 | 0 7 1 |
| 8 | 5 1 2 | 7 2 -1 | -2 3 5 | 3 4 7 |
| 9 | 3 2 1 | 4 -1 1 | -3 2 3 | 0 4 4 |
| 10 | 2 3 2 | 3 -2 5 | -3 5 -6 | 5 1 7 |
2. Найти решение системы линейных уравнений 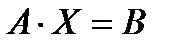 , пользуясь методом Гаусса, по вариантам задания 1.
, пользуясь методом Гаусса, по вариантам задания 1.
3. Найти решение системы линейных уравнений 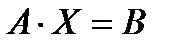 , пользуясь матричным методом, по вариантам задания 1. Произвести проверку вычисления обратной матрицы.
, пользуясь матричным методом, по вариантам задания 1. Произвести проверку вычисления обратной матрицы.
4. Найти предел функции.
4.1. 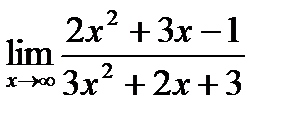
| 4.5. 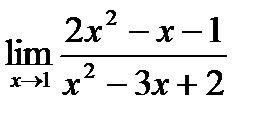
| 4.8. 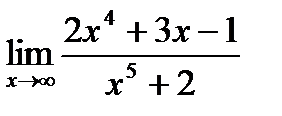
|
4.2. 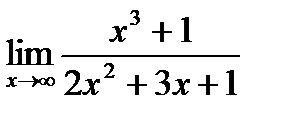
| 4.6. 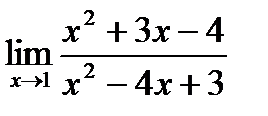
| 4.9. 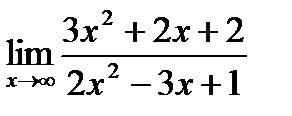
|
4.3. 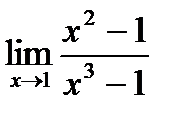
| 4.7. 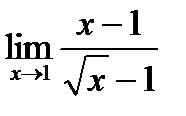
| 4.10. 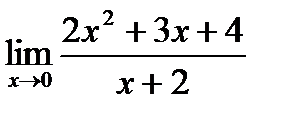
|
4.4. 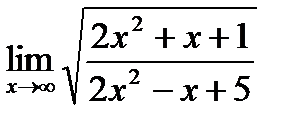
|
5. Найти предел функции:
5.1. 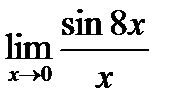
| 5.5. 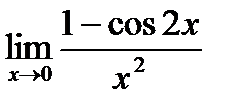
| 5.8. 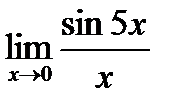
|
5.2. 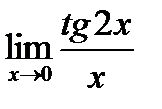
| 5.6. 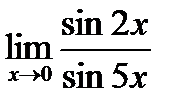
| 5.9. 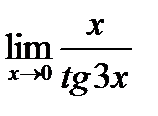
|
5.3. 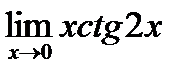
| 5.7. 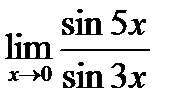
| 5.10. 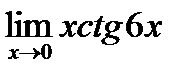
|
5.4. 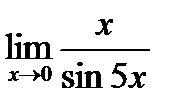
|
6. Найти предел функции:
6.1. 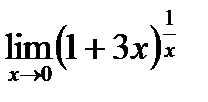
| 6.5. 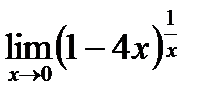
| 6.8. 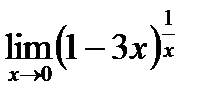
|
6.2. 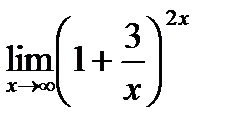
| 6.6. 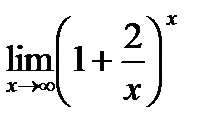
| 6.9. 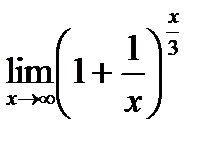
|
6.3. 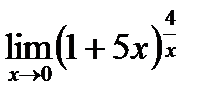
| 6.7. 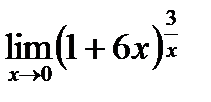
| 6.10. 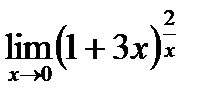
|
6.4. 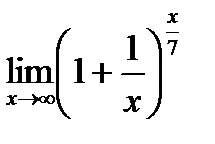
|
7. Найти производные функций:
7.1. 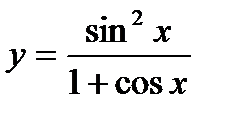
| 7.5. 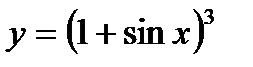
| 7.8. 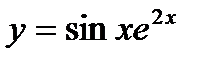
|
7.2. 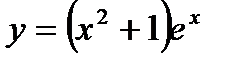
| 7.6. 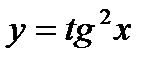
| 7.9. 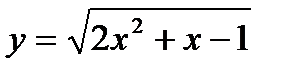
|
7.3. 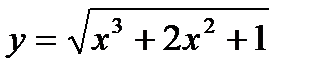
| 7.7. 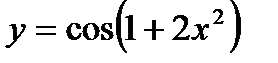
| 7.10. 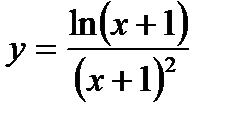
|
7.4. 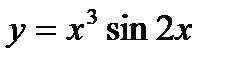
|
8. Вычислить определенный интеграл:
8.1. 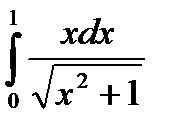
| 8.5. 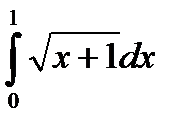
| 8.8. 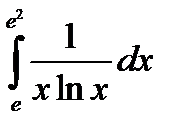
|
8.2. 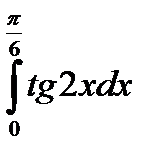
| 8.6. 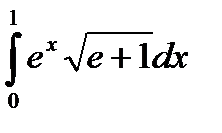
| 8.9. 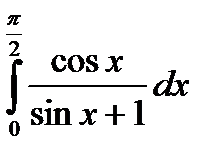
|
8.3. 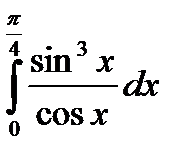
| 8.7. 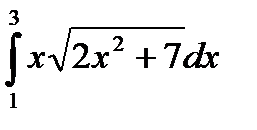
| 8.10. 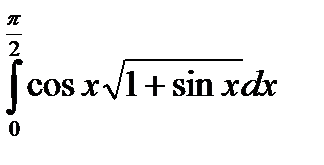
|
8.4. 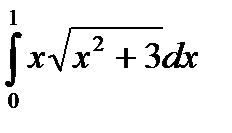
|
9. Вычислить значение функции 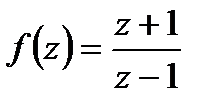 в точке
в точке 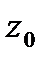 . Записать ответ в алгебраической, тригонометрической и показательной формах.
. Записать ответ в алгебраической, тригонометрической и показательной формах.
9.1. 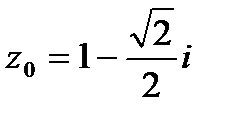
| 9.5. 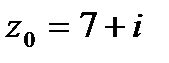
| 9.8. 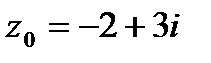
|
9.2. 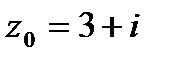
| 9.6. 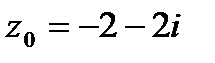
| 9.9. 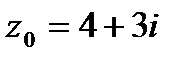
|
9.3. 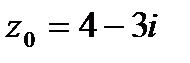
| 9.7. 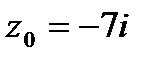
| 9.10. 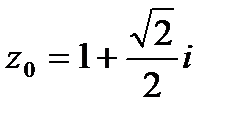
|
9.4. 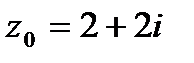
|
10. Найти 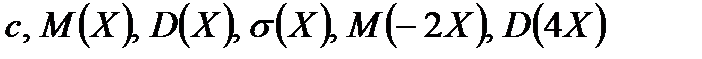 , если закон распределения дискретной случайной величины задан таблично:
, если закон распределения дискретной случайной величины задан таблично:
10.1.
| xi | -2 | -1 | 0 | 1 | 2 | 3 |
| pi | 0,1 | 0,2 | 0,25 | с | 0,1 | 0,2 |
10.2.
| xi | -2 | -1 | 0 | 1 | 2 | 3 |
| pi | с | 0,25 | 0,15 | 0,2 | 0,1 | 0,1 |
10.3.
| xi | -3 | -1 | 0 | 1 | 2 |
| pi | 0,2 | 0,1 | 0,15 | с | 0,3 |
10.4.
| xi | 0 | 1 | 2 | 3 | 4 |
| pi | 0,35 | 0,2 | 0,15 | с | 0,1 |
10.5.
| xi | -1 | 0 | 1 | 2 | 3 |
| pi | с | 0,1 | 0,4 | 0,1 | 0,15 |
10.6.
| xi | -2 | -1 | 0 | 1 | 2 |
| pi | 0,25 | 0,1 | с | 0,3 | 0,1 |
10.7.
| xi | -3 | -2 | -1 | 0 | 1 |
| pi | 0,15 | 0,1 | 0,2 | 0,1 | с |
10.8.
| xi | -1 | 0 | 1 | 2 | 3 |
| pi | с | 0,25 | 0,35 | 0,1 | 0,1 |
10.9.
| xi | -2 | 0 | 2 | 3 | 4 |
| pi | 0,1 | 0,2 | 0,25 | с | 0,1 |
10.10.
| xi | 0 | 1 | 2 | 3 | 4 |
| pi | 0,15 | с | 0,1 | 0,2 | 0,15 |
Дата: 2018-11-18, просмотров: 321.