Определение. Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных элементарных исходов опыта.
Вероятность события А обозначают через Р(А). Если через т обозначить число элементарных исходов, благоприятствующих событию А, а через п – число всех равновозможных элементарных исходов опыта, образующих полную группу событий, то 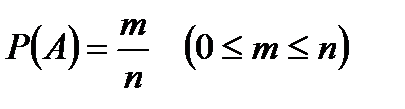 .
.
Законом распределения дискретной случайной величины называется соответствие между значениями х1, х2, х3, … этой величины и их вероятностями р1, р2, р3, …
Например, если дискретная случайная величина Х принимает конечное множество значений х1, х2, х3, …, х n с вероятностями р1, р2, р3, …, р n соответственно, то ее закон распределения определяется числами
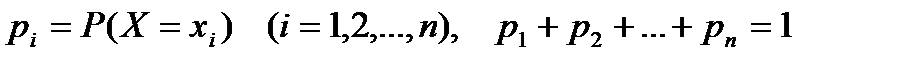 .
.
Определение. Математическим ожиданием или средним значением дискретной случайной величины Х с законом распределения
| Х | x1 | x2 | x3 | … | xn |
| Р | р1 | р2 | р3 | … | р n |
называется число 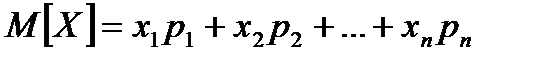 .
.
Определение. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Обозначим дисперсию случайной величины через 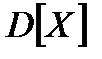 , тогда согласно определению будем иметь
, тогда согласно определению будем иметь 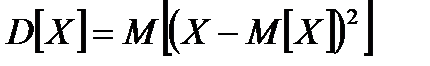 .
.
Средним квадратичным отклонением случайной величины Х называется величина 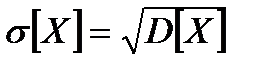 .
.
Формулы комбинаторики
1. Размещения: 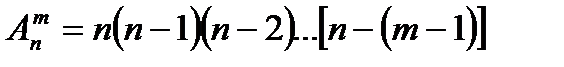 .
.
2. Перестановки: 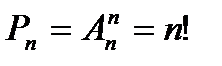
3. Сочетания: 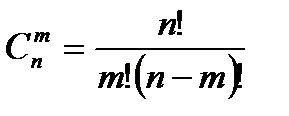
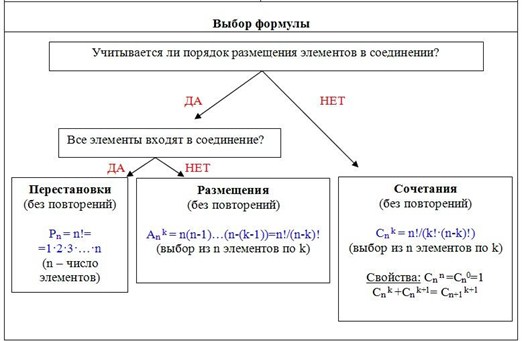
Большинство комбинаторных задач решается с помощью двух основных правил – правила суммы и правила произведения. Выбор правила:
| Правило суммы | Правило произведения |
| Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор объекта либо А, либо В можно осуществить (m + n) способами. | Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары А и В можно осуществить (m · n) способами. |
Практическая работа №6
Тема: Решение простейших задач математической статистики и теории вероятностей
Цель работы: Научиться решать простейшие задачи математической статистики и теории вероятностей
Задания.
1. Найдите число размещений:
1.1 а) 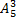 ; б) t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>3</m:t></m:r></m:sub><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
; б) t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>3</m:t></m:r></m:sub><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 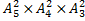 .
.
1.2 а) 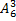 ; б)
; б) 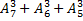 .
.
1.3 а) 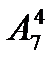 ; б)
; б) 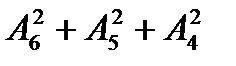 .
.
2. Вычислите:
2.1 а) 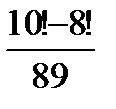 ; б)
; б) 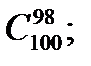
2.2 а) 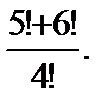 б)
б) 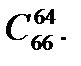
2.3 а) 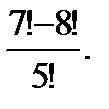 б)
б) 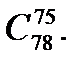
3. Решите уравнение:
3.1 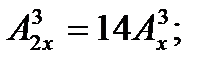 3.2
3.2 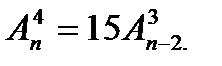 3.3
3.3 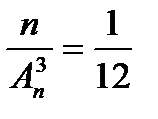 .
.
4. Составьте всевозможные перестановки из элементов:
4.1 a, b, c, d 4.2 1, 2, 3, 4 4.3 к, ш, м, о
Задание 5.
5.1 В партии из 12 деталей имеется 7 стандартных. Найти вероятность того, что среди шести взятых наугад деталей 4 стандартных.
5.2 На стеллаже 15 учебников, 5 из них в переплете. Наудачу выбираются 3 учебника. Какова вероятность, что хотя бы один из них будет в переплете?
5.3 В урне находятся 15 белых и 6 черных шаров. Из нее вынимают наугад один шар, снова возвращают его в урну и шары перемешивают. Найдите вероятность того, что оба вынутых шара белые.
Задание 6. Закон распределения случайной величины Х задан таблично. Вычислите математическое ожидание, дисперсию и среднее квадратичное отклонение заданной случайной величины. Постройте многоугольник распределения.
6.1
| х | -2 | -1 | 1 | 2 | 3 |
| р | 0,3 | 0,1 | 0,2 | 0,1 | р5 |
6.2
| х | -2 | -1 | 1 | 2 |
| р | 0,1 | р2 | 0,5 | 0,2 |
6.3
| х | -1 | 1 | 2 | 3 |
| р | 0,1 | 0,2 | 0,1 | р4 |
Тема «Комплексные числа»
Дата: 2018-11-18, просмотров: 337.