Содержание
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Аннотация
Рабочая тетрадь по дисциплине «Математика» предназначена для использования на практических занятиях и составлена в соответствии с рабочей программой дисциплины.
В рабочей тетради приведены материалы для практических работ, а также задания контрольной самостоятельной работы для студентов. Задания имеют двойную нумерацию: первое число – номер задания, второе число – номер варианта.
Практические работы составлены в трех вариантах.
Выбор варианта практической работы определяется в зависимости от первой буквы фамилии студента по таблице:
| Первая буква фамилии | А, Г, Ё, И, Л, О, С, Ф, Ч, Э | Б, Д, Ж, Й, М, П, Т, Х, Ш, Ю | В, Е, З, К, Н, Р, У, Ц, Щ, Я |
| Номер варианта | 1 | 2 | 3 |
Контрольная самостоятельная работа составлена в десяти вариантах.
Выбор варианта контрольной работы определяется в зависимости от первой буквы фамилии студента по таблице:
| Первая буква фамилии | А, К, Ф | Б, Л, Х | В, М, Ц | Г, Н, Ч | Д, О, Ш | Е, П, Щ | Ё, Р, Э | Ж, С, Ю | З, Т, Я | И, Й, У |
| Номер варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Тема «Предел функции»
Тема «Производная функции»
Практическая работа № 1
Тема: Вычисление предела функции и производной функции
Цель работы: Сформировать навыки вычисления пределов и производных функции, раскрытия неопределенностей типа 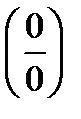 ,
, 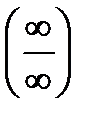 , использования первого и второго замечательных пределов
, использования первого и второго замечательных пределов
Задания
1. Вычислить пределы функций:
1.1. а) 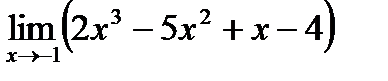 ;
б) ;
б) 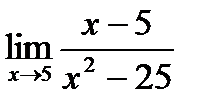 ;
в) ;
в) 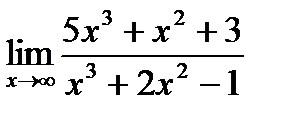 ;
г) ;
г) 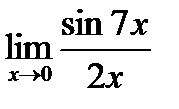 ;
д) ;
д) 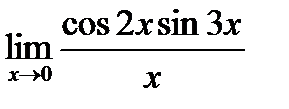 ;
е) ;
е) 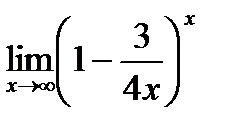 ;
ж) ;
ж) 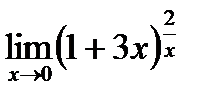 . .
| 1.2. а) 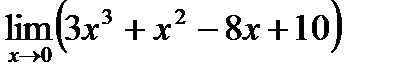 ;
б) ;
б) 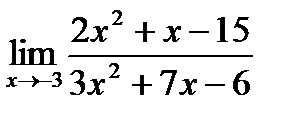 ;
в) ;
в) 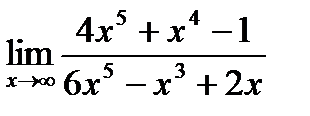 ;
г) ;
г) 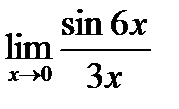 ;
д) ;
д) 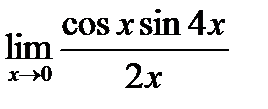 ;
е) ;
е) 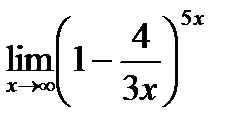 ;
ж) ;
ж) 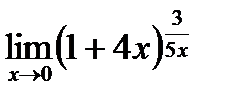 . .
| 1.3. а) 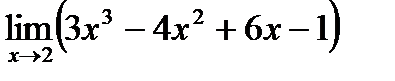 ;
б) ;
б) 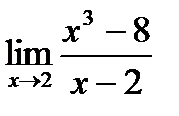 ;
в) ;
в) 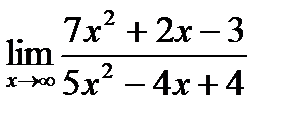 ;
г) ;
г) 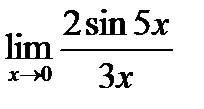 ;
д) ;
д) 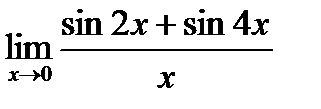 ;
е) ;
е) 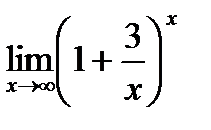 ;
ж) ;
ж) 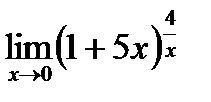 . .
|
2. Вычислите производную 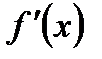 при данном значении аргумента х:
при данном значении аргумента х:
2.1
а) 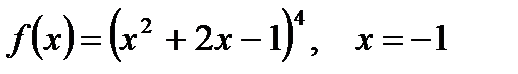
| 2.2
а) 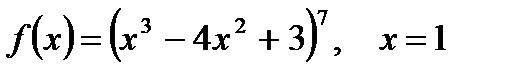
| 2.3
а) 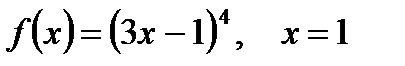
|
б) 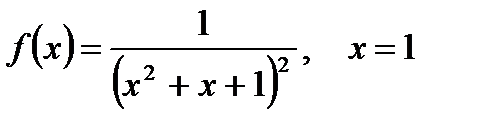
| б) 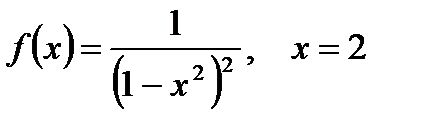
| б) 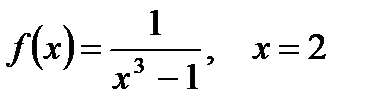
|
в) 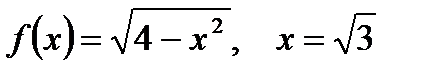
| в) 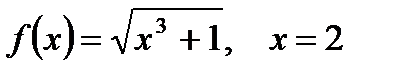
| в) 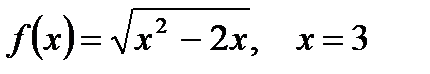
|
г) 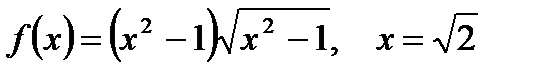
| г) 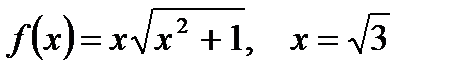
| г) 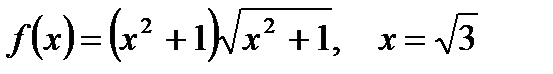
|
д) 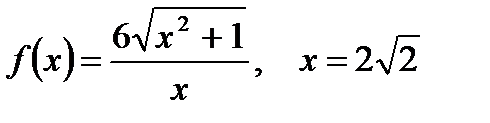
| д) 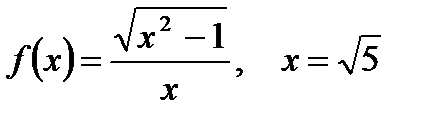
| д) 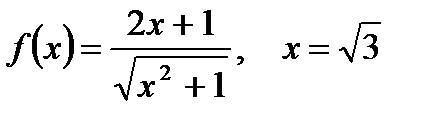
|
е) 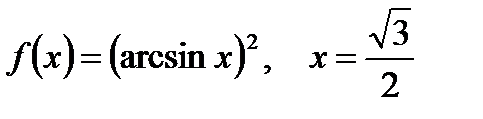 . .
| е) 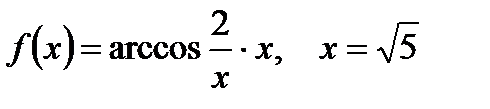
| е) 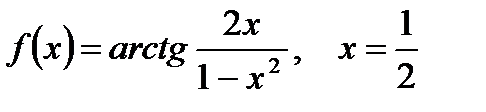
|
Тема «Интегрирование функций»
Практическая работа № 2
Тема: Вычисление интегралов различными методами
Цель работы: Формирование умений и навыков при вычислении интегралов, используя основные формулы для вычисления табличных интегралов, применение методов интегрирования заменой переменной и интегрирования по частям
Задания.
1. Вычислить интегралы, применяя формулы интегрирования
| 1.1. | а) 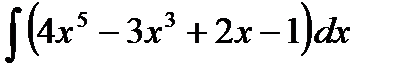 ; ;
| б) 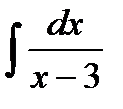 ; ;
| в) 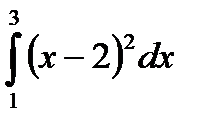 ; ;
| г) 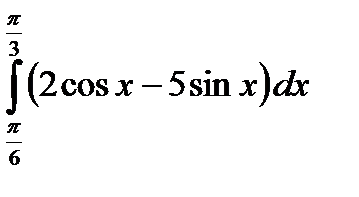 . .
|
| 1.2. | а) 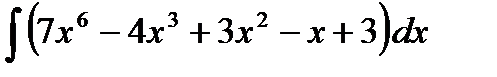 ; ;
| б) 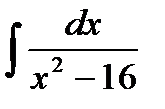 ; ;
| в) 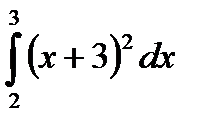 ; ;
| г) 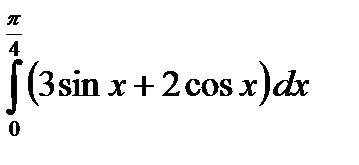 . .
|
| 1.3. | а) 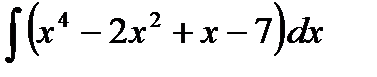 ; ;
| б) 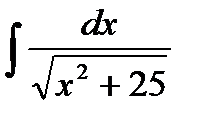
| в) 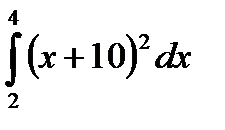 ; ;
| г) 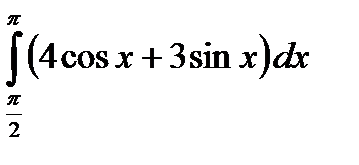 . .
|
2. Используя метод замены переменной, найти следующие интегралы
| 2.1. | а) 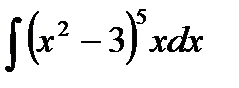 ; ;
| б) 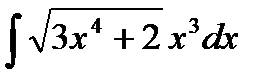 ; ;
|
в) 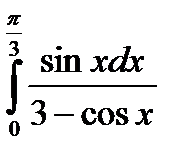
| г) 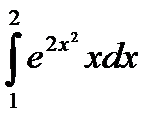 . .
| |
| 2.2. | а) 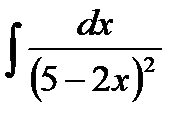 ; ;
| б) 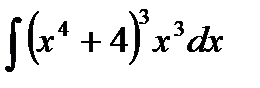 ; ;
|
в) 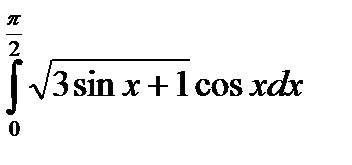
| г) 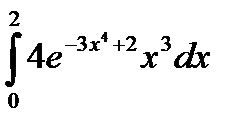 . .
| |
| 2.3. | а) 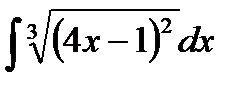 ; ;
| б) 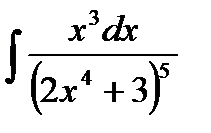 ; ;
|
в) 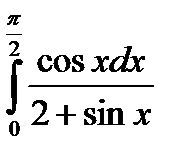
| г) 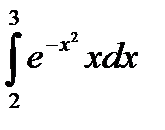 . .
|
3. Используя метод интегрирования по частям, найти интегралы.
3.1. а) 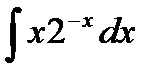 ; б)
; б) 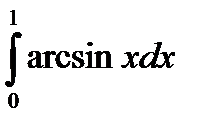 .
.
3.2. а) 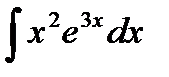 ; б)
; б) 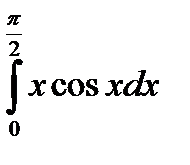 .
.
3.3. а) 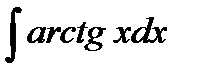 ; б)
; б) 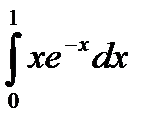 .
.
Практическая работа № 3
Тема: Решение дифференциальных уравнений первого и второго порядков
Цель работы: Научиться находить общие и частные решения уравнений первого порядка и второго порядков
Задания
1. Найти общее решение уравнений:
1.1 а) 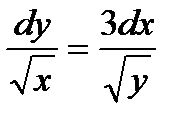 ;
б) ;
б) 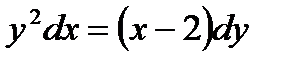 . .
| 1.2 а) 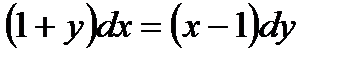 ;
б) ;
б) 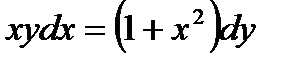 . .
| 1.3 а) 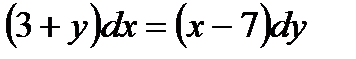 ;
б) ;
б) 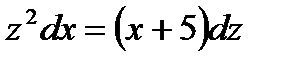 . .
|
2. Найти частные решения уравнений, удовлетворяющие указанным начальным условиям:
2.1 а) 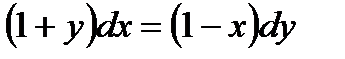 ,
, 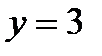 при
при 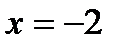 ;
;
б) 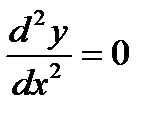 ;
; 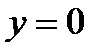 при
при 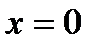 ;
; 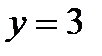 при
при 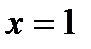 .
.
2.2 а) 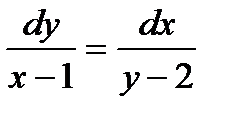
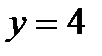 при
при 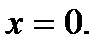
б) 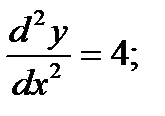
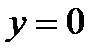 при
при 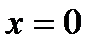 ;
; 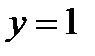 при
при 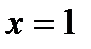 .
.
2.3 а) 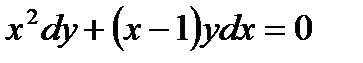 ,
, 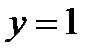 при
при 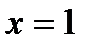 .
.
б) 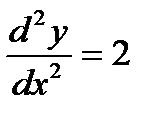 ;
; 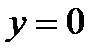 при
при 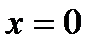 ;
; 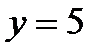 при
при 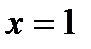 .
.
3. Найти общее решение уравнений:
3.1 а) 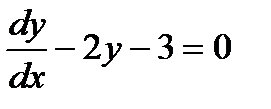 .
.
3.2 а) 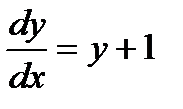 .
.
3.3 а) 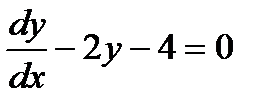 .
.
4. Решите уравнения:
4.1 а) 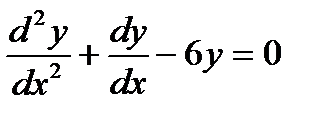 ; б)
; б) 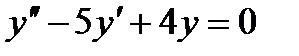 .
.
4.2 а) 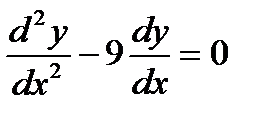 ; б)
; б) 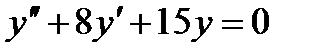 .
.
4.3 а) 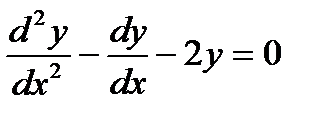 ; б)
; б) 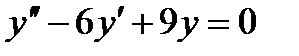 .
.
Практическая работа №4
Тема: Действия над матрицами. Вычисление определителей.
Цель работы: Научиться выполнять операции над матрицами, вычислять определители 2-го и 3-его порядка.
Задания.
1. Умножить данную матрицу А на число λ
1.1. 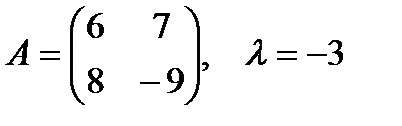
1.2. 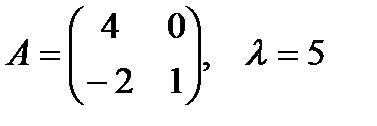
1.3. 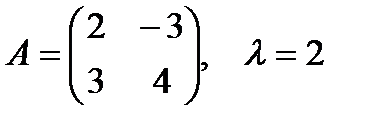
2. Найти сумму матриц A и B
2.1. 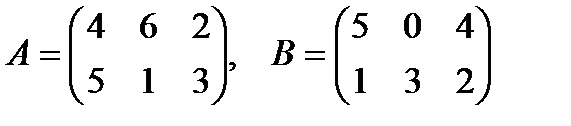
2.2. 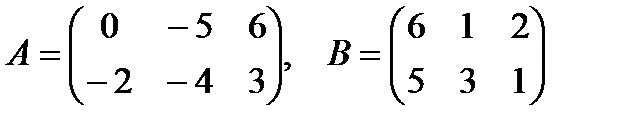
2.3. 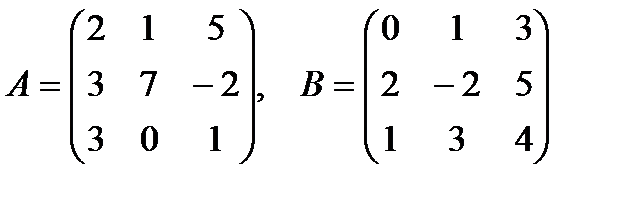
3. Найти произведение A 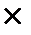 B, где
B, где
3.1. 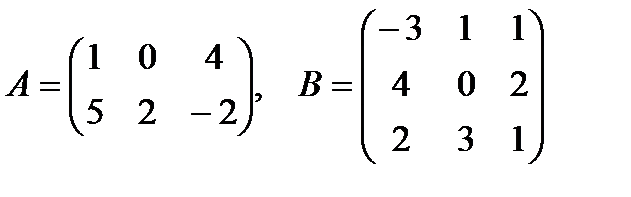
3.2. 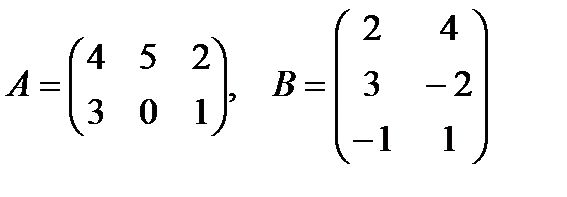
3.3. 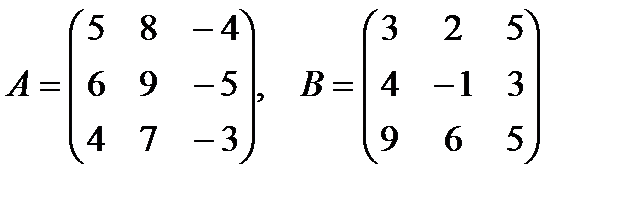
4. Вычислить линейные комбинации с матрицами A и B
4.1. 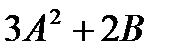 , если
, если 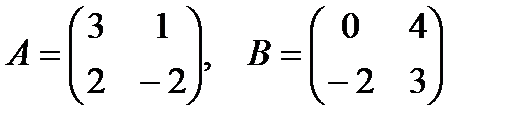
4.2. 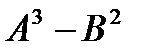 , если
, если 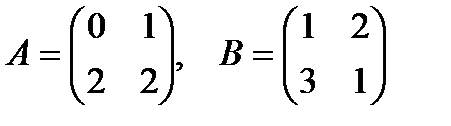
4.3. 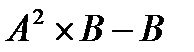 , если
, если 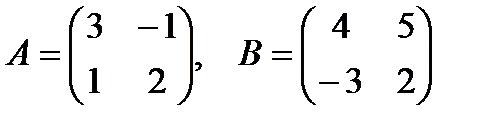
5. Вычислить определитель второго и третьего порядка
5.1. а) 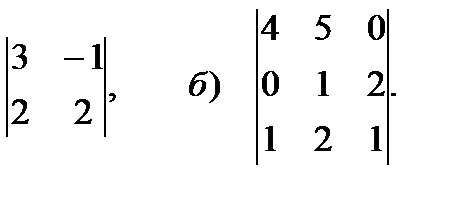
5.2. а) 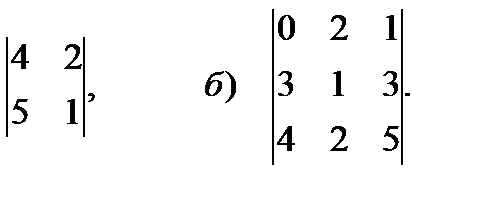
5.3. а) 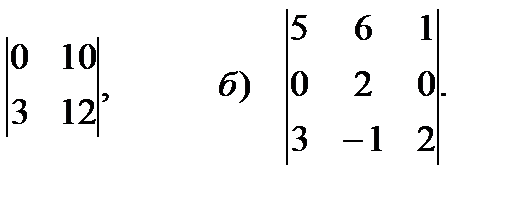
Практическая работа № 5.
Тема: Решение систем линейных уравнений различными методами
Цель работы: Формирование навыков решения линейных уравнений по правилу Крамера, методом Гаусса и методом обратной матрицы.
Задания.
1. Решить систему уравнений:
а) методом обратной матрицы; б) по формулам Крамера
1.1 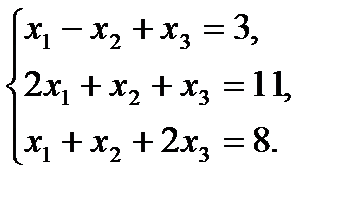
1.2 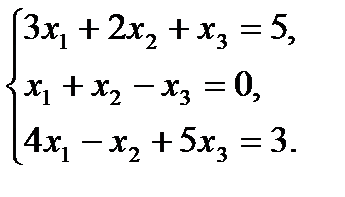
1.3 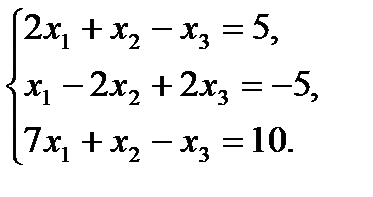
2. Решить систему уравнений методом Гаусса:
2.1 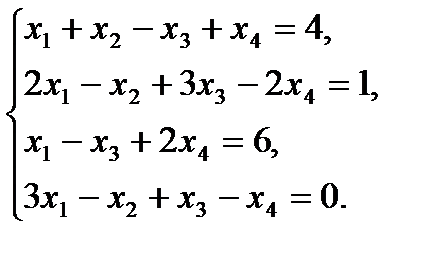
2.2 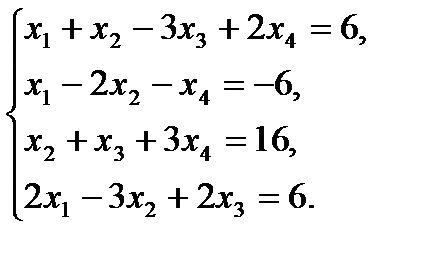
2.3 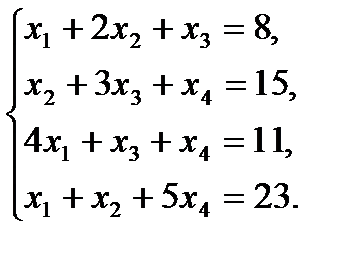
Практическая работа №6
Тема: Решение простейших задач математической статистики и теории вероятностей
Цель работы: Научиться решать простейшие задачи математической статистики и теории вероятностей
Задания.
1. Найдите число размещений:
1.1 а) 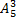 ; б) t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>3</m:t></m:r></m:sub><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
; б) t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>3</m:t></m:r></m:sub><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 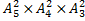 .
.
1.2 а) 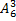 ; б)
; б) 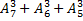 .
.
1.3 а) 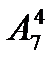 ; б)
; б) 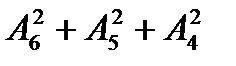 .
.
2. Вычислите:
2.1 а) 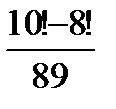 ; б)
; б) 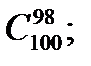
2.2 а) 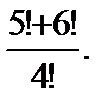 б)
б) 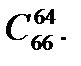
2.3 а) 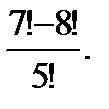 б)
б) 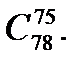
3. Решите уравнение:
3.1 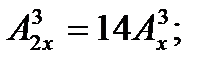 3.2
3.2 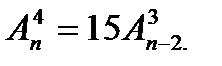 3.3
3.3 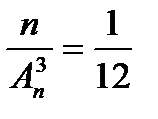 .
.
4. Составьте всевозможные перестановки из элементов:
4.1 a, b, c, d 4.2 1, 2, 3, 4 4.3 к, ш, м, о
Задание 5.
5.1 В партии из 12 деталей имеется 7 стандартных. Найти вероятность того, что среди шести взятых наугад деталей 4 стандартных.
5.2 На стеллаже 15 учебников, 5 из них в переплете. Наудачу выбираются 3 учебника. Какова вероятность, что хотя бы один из них будет в переплете?
5.3 В урне находятся 15 белых и 6 черных шаров. Из нее вынимают наугад один шар, снова возвращают его в урну и шары перемешивают. Найдите вероятность того, что оба вынутых шара белые.
Задание 6. Закон распределения случайной величины Х задан таблично. Вычислите математическое ожидание, дисперсию и среднее квадратичное отклонение заданной случайной величины. Постройте многоугольник распределения.
6.1
| х | -2 | -1 | 1 | 2 | 3 |
| р | 0,3 | 0,1 | 0,2 | 0,1 | р5 |
6.2
| х | -2 | -1 | 1 | 2 |
| р | 0,1 | р2 | 0,5 | 0,2 |
6.3
| х | -1 | 1 | 2 | 3 |
| р | 0,1 | 0,2 | 0,1 | р4 |
Тема «Комплексные числа»
Практическая работа №7
Тема: Выполнение действий над комплексными числами
Цель работы: Формирование навыков при выполнении действий над комплексными числам, заданными в алгебраической форме
Задания.
1. Построить на плоскости точки, изображающие следующие комплексные числа:
1.1. а) 3 + 2i, б) 5, в) -4i
1.2. а) 2 + 4i, б) -3, в) 4i
1.3. а) -1 + 2i, б) 6i, в) 4.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел:
2.1. 9 + 2ix + 4iy = 10i + 5x - 6y
2.2. 2ix + 3iy + 17 = 3x + 2y - 18i
2.3. 5x – 2y + (x + y)i = 4 + 5i .
3. Найти модуль и главное значение аргумента комплексного числа:
3.1. -2 - 2i
3.2. 1 + i 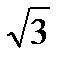
3.3. - 3i .
4. Выполнить действия:
4.1. а) 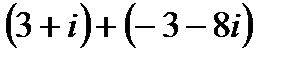
б) 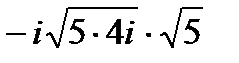
в) 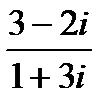
4.2 а) 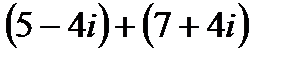
б) 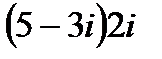
в) 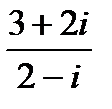
4.3 а) 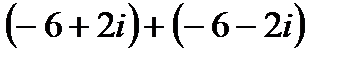
б) 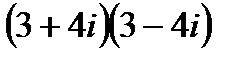
в) 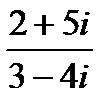
Практическая работа № 8
Тема: Операции над множествами
Цель работы: Формирование навыков задания множеств различными способами, выполнение действий над множествами
Задания.
1. Составить список элементов множества, заданного следующим образом:
1.1 а) 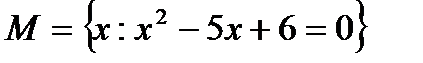 ; б)
; б) 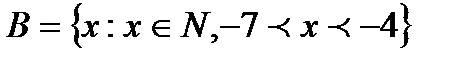 .
.
1.2 а) 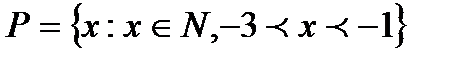 ; б)
; б) 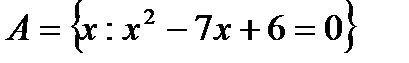 .
.
1.3 а) 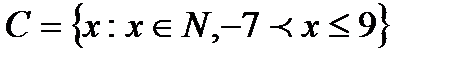 ; б)
; б) 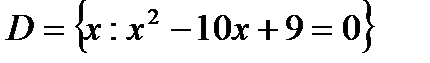 .
.
2. Найти объединение и пересечение множеств:
2.1 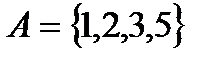 и
и 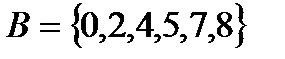 .
.
2.2 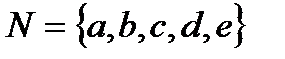 и
и 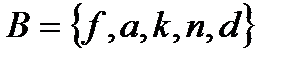 .
.
2.3 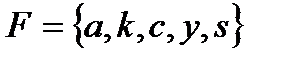 и
и 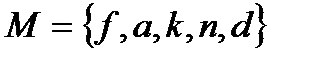 .
.
3. Выписав все подмножества заданного множества, подсчитайте их число:
3.1 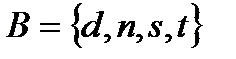 . 3.2
. 3.2 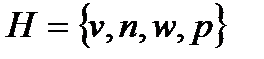 . 3.3
. 3.3 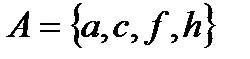 .
.
4. Выполните операции с заданными множествами:
4.1 а) 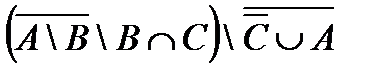 ; б)
; б) 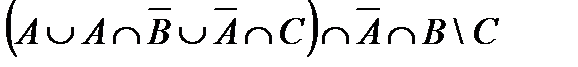 , где
, где 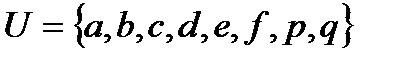 ,
, 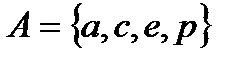 ,
, 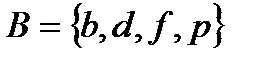 ,
, 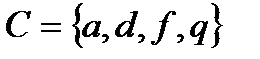 .
.
4.2 а) 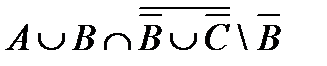 ; б)
; б) 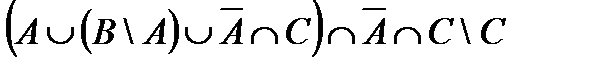 , где
, где 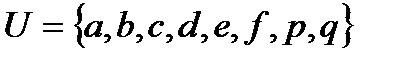 ,
, 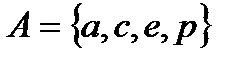 ,
, 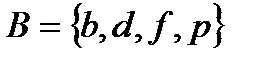 ,
, 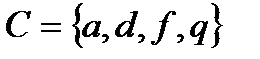 .
.
4.3 а) 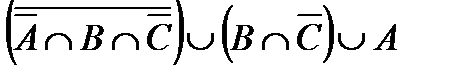 ; б)
; б) 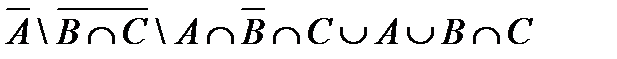 , где
, где 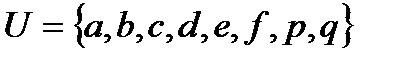 ,
, 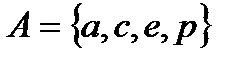 ,
, 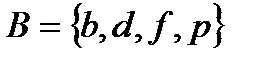 ,
, 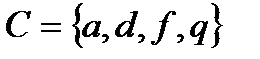 .
.
5. С помощью диаграмм Эйлера-Венна упростите выражение:
5.1 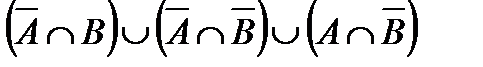 .
.
5.2 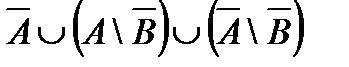 .
.
5.3 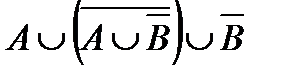 .
.
Примечание: Сначала выполняется операция дополнения (  ), затем пересечения
), затем пересечения 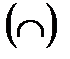 и только затем объединения
и только затем объединения 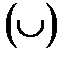 и разности
и разности 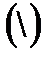 . Для изменения этого порядка в выражении используются скобки.
. Для изменения этого порядка в выражении используются скобки.
Контрольная самостоятельная работа
1. Найти решение системы линейных уравнений 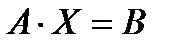 , пользуясь правилом Крамера.
, пользуясь правилом Крамера.
Варианты заданий
| Номер варианта | Матрица А коэффициентов системы | Столбец В свободных членов | ||
| 1 | 1 3 2 | 2 1 -1 | 1 4 1 | 3 5 -1 |
| 2 | 2 3 2 | -3 1 3 | 4 -2 -2 | 1 -1 1 |
| 3 | 5 6 2 | -2 4 -1 | 5 -2 4 | 3 2 3 |
| 4 | 2 3 5 | -1 7 4 | 6 -3 -5 | 1 10 9 |
| 5 | 3 5 3 | -2 -6 2 | 5 2 -3 | 6 1 2 |
| 6 | 2 3 1 | 5 -2 -2 | -3 2 4 | 4 3 3 |
| 7 | 1 2 3 | 3 -1 2 | -1 5 -2 | 0 7 1 |
| 8 | 5 1 2 | 7 2 -1 | -2 3 5 | 3 4 7 |
| 9 | 3 2 1 | 4 -1 1 | -3 2 3 | 0 4 4 |
| 10 | 2 3 2 | 3 -2 5 | -3 5 -6 | 5 1 7 |
2. Найти решение системы линейных уравнений 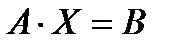 , пользуясь методом Гаусса, по вариантам задания 1.
, пользуясь методом Гаусса, по вариантам задания 1.
3. Найти решение системы линейных уравнений 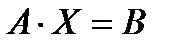 , пользуясь матричным методом, по вариантам задания 1. Произвести проверку вычисления обратной матрицы.
, пользуясь матричным методом, по вариантам задания 1. Произвести проверку вычисления обратной матрицы.
4. Найти предел функции.
4.1. 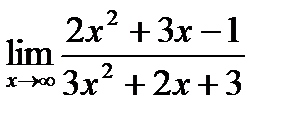
| 4.5. 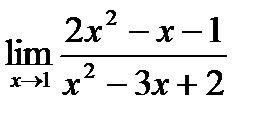
| 4.8. 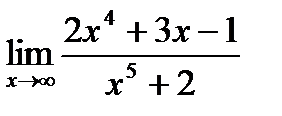
|
4.2. 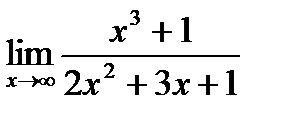
| 4.6. 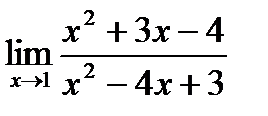
| 4.9. 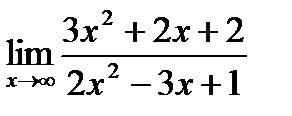
|
4.3. 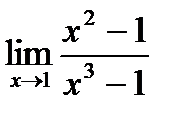
| 4.7. 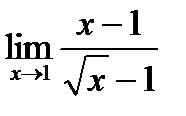
| 4.10. 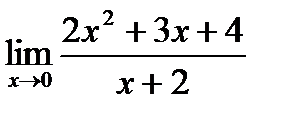
|
4.4. 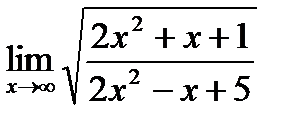
|
5. Найти предел функции:
5.1. 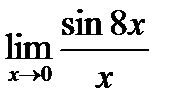
| 5.5. 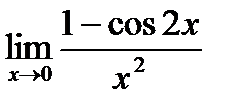
| 5.8. 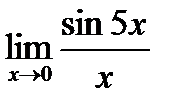
|
5.2. 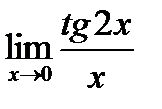
| 5.6. 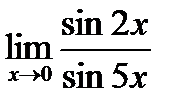
| 5.9. 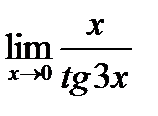
|
5.3. 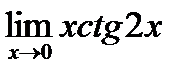
| 5.7. 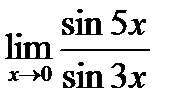
| 5.10. 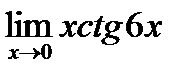
|
5.4. 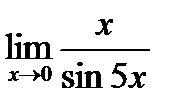
|
6. Найти предел функции:
6.1. 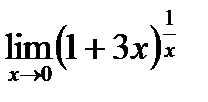
| 6.5. 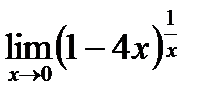
| 6.8. 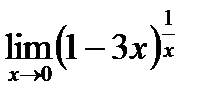
|
6.2. 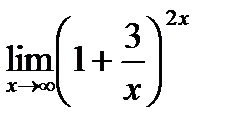
| 6.6. 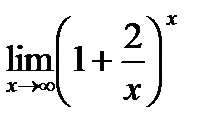
| 6.9. 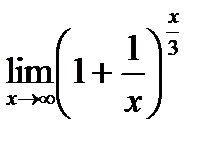
|
6.3. 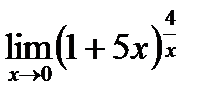
| 6.7. 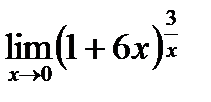
| 6.10. 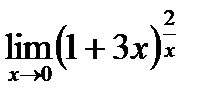
|
6.4. 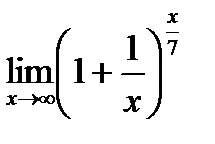
|
7. Найти производные функций:
7.1. 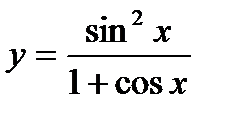
| 7.5. 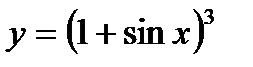
| 7.8. 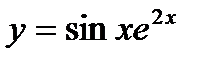
|
7.2. 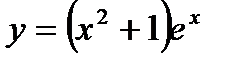
| 7.6. 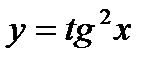
| 7.9. 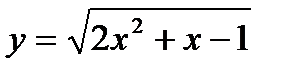
|
7.3. 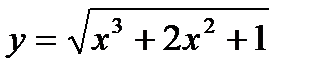
| 7.7. 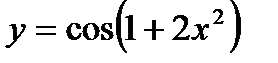
| 7.10. 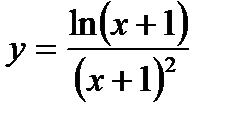
|
7.4. 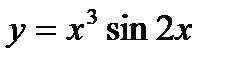
|
8. Вычислить определенный интеграл:
8.1. 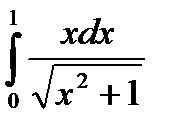
| 8.5. 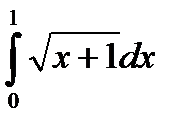
| 8.8. 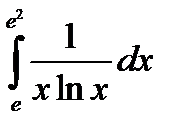
|
8.2. 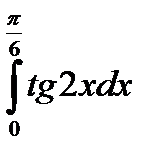
| 8.6. 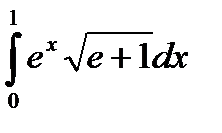
| 8.9. 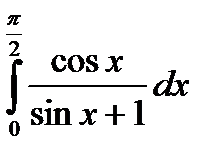
|
8.3. 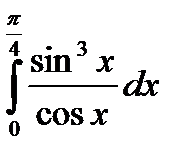
| 8.7. 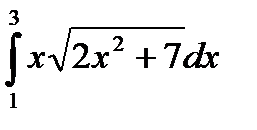
| 8.10. 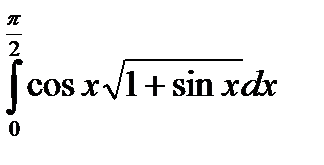
|
8.4. 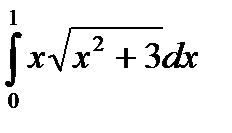
|
9. Вычислить значение функции 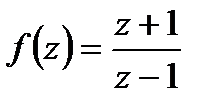 в точке
в точке 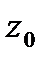 . Записать ответ в алгебраической, тригонометрической и показательной формах.
. Записать ответ в алгебраической, тригонометрической и показательной формах.
9.1. 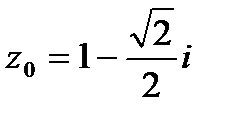
| 9.5. 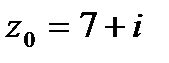
| 9.8. 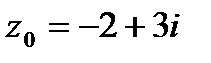
|
9.2. 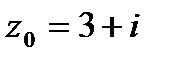
| 9.6. 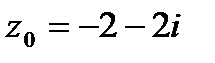
| 9.9. 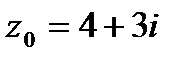
|
9.3. 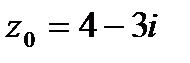
| 9.7. 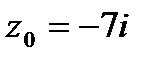
| 9.10. 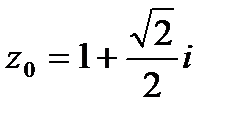
|
9.4. 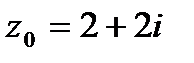
|
10. Найти 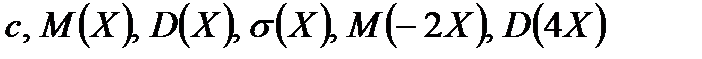 , если закон распределения дискретной случайной величины задан таблично:
, если закон распределения дискретной случайной величины задан таблично:
10.1.
| xi | -2 | -1 | 0 | 1 | 2 | 3 |
| pi | 0,1 | 0,2 | 0,25 | с | 0,1 | 0,2 |
10.2.
| xi | -2 | -1 | 0 | 1 | 2 | 3 |
| pi | с | 0,25 | 0,15 | 0,2 | 0,1 | 0,1 |
10.3.
| xi | -3 | -1 | 0 | 1 | 2 |
| pi | 0,2 | 0,1 | 0,15 | с | 0,3 |
10.4.
| xi | 0 | 1 | 2 | 3 | 4 |
| pi | 0,35 | 0,2 | 0,15 | с | 0,1 |
10.5.
| xi | -1 | 0 | 1 | 2 | 3 |
| pi | с | 0,1 | 0,4 | 0,1 | 0,15 |
10.6.
| xi | -2 | -1 | 0 | 1 | 2 |
| pi | 0,25 | 0,1 | с | 0,3 | 0,1 |
10.7.
| xi | -3 | -2 | -1 | 0 | 1 |
| pi | 0,15 | 0,1 | 0,2 | 0,1 | с |
10.8.
| xi | -1 | 0 | 1 | 2 | 3 |
| pi | с | 0,25 | 0,35 | 0,1 | 0,1 |
10.9.
| xi | -2 | 0 | 2 | 3 | 4 |
| pi | 0,1 | 0,2 | 0,25 | с | 0,1 |
10.10.
| xi | 0 | 1 | 2 | 3 | 4 |
| pi | 0,15 | с | 0,1 | 0,2 | 0,15 |
Содержание
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Аннотация
Рабочая тетрадь по дисциплине «Математика» предназначена для использования на практических занятиях и составлена в соответствии с рабочей программой дисциплины.
В рабочей тетради приведены материалы для практических работ, а также задания контрольной самостоятельной работы для студентов. Задания имеют двойную нумерацию: первое число – номер задания, второе число – номер варианта.
Практические работы составлены в трех вариантах.
Выбор варианта практической работы определяется в зависимости от первой буквы фамилии студента по таблице:
| Первая буква фамилии | А, Г, Ё, И, Л, О, С, Ф, Ч, Э | Б, Д, Ж, Й, М, П, Т, Х, Ш, Ю | В, Е, З, К, Н, Р, У, Ц, Щ, Я |
| Номер варианта | 1 | 2 | 3 |
Контрольная самостоятельная работа составлена в десяти вариантах.
Выбор варианта контрольной работы определяется в зависимости от первой буквы фамилии студента по таблице:
| Первая буква фамилии | А, К, Ф | Б, Л, Х | В, М, Ц | Г, Н, Ч | Д, О, Ш | Е, П, Щ | Ё, Р, Э | Ж, С, Ю | З, Т, Я | И, Й, У |
| Номер варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Тема «Предел функции»
Краткие теоретические сведения
Определение. Число А называется пределом функции 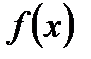 в точке
в точке 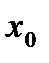 и обозначается
и обозначается 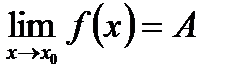 , если для любого числа
, если для любого числа 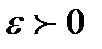 существует число
существует число 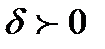 такое, что для всех х, удовлетворяющих условию
такое, что для всех х, удовлетворяющих условию 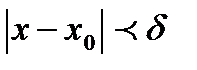 , где
, где 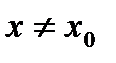 , выполняется неравенство
, выполняется неравенство 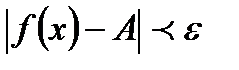 .
.
При вычислении пределов функции используются теоремы:
Теорема 1. Если существуют пределы функций 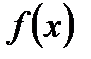 и
и 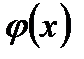 при
при 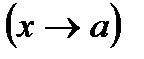 , то существует также и предел их суммы, равный сумме пределов функций
, то существует также и предел их суммы, равный сумме пределов функций 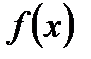 и
и 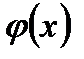 :
:
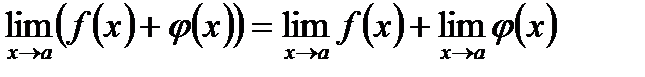 .
.
Теорема 2. Если существуют пределы функций 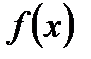 и
и 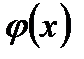 при
при 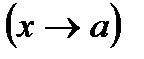 , то существует также и предел их произведения, равный произведению пределов функций
, то существует также и предел их произведения, равный произведению пределов функций 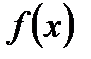 и
и 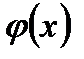 :
:
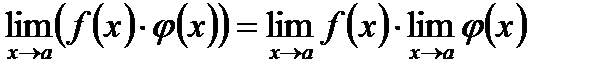 .
.
Теорема 3. Если существуют пределы функций 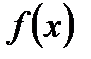 и
и 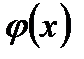 при
при 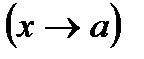 , предел функции
, предел функции 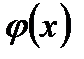 отличен от нуля, то существует также и предел отношения, равный отношению пределов функций
отличен от нуля, то существует также и предел отношения, равный отношению пределов функций 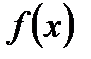 и
и 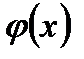 :
:
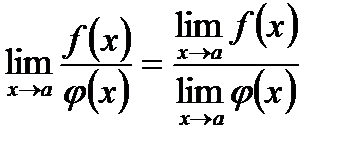 .
.
Следствие 1. Постоянный множитель можно вынести за знак предела:
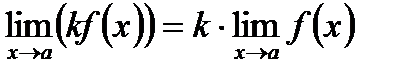 .
.
Следствие 2. Если n - натуральное число, то справедливы соотношения: 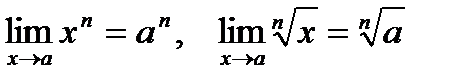 .
.
Следствие 3. Предел многочлена (целой рациональной функции)
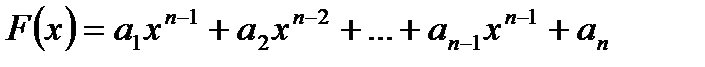 при
при 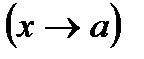 равен значению этого многочлена при х = а, т.е.
равен значению этого многочлена при х = а, т.е. 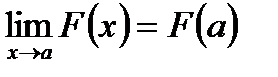 .
.
Следствие 4. Предел дробно – рациональной функции
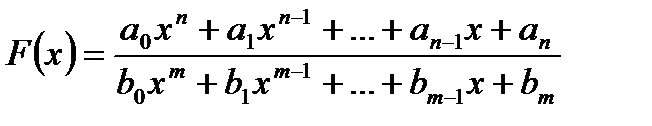
при 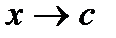 равен значению этой функции при х = с, если с принадлежит области определения этой функции, т.е.
равен значению этой функции при х = с, если с принадлежит области определения этой функции, т.е. 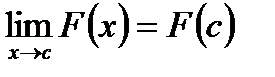 .
.
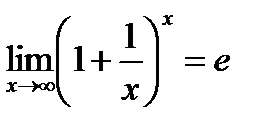 Первый замечательный предел: Второй замечательный предел:
Первый замечательный предел: Второй замечательный предел:
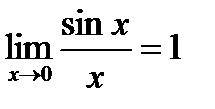
Тема «Производная функции»
Дата: 2018-11-18, просмотров: 356.