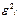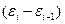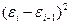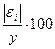Если D[ε] ≠ 0, то используют метод Гольдфельда-Квандта:
- необходимо ранжировать переменную xi;
- разделить полученную совокупность на две части;
- по каждой группе построить уравнение регрессии;
- определить остаточные суммы квадратов по формулам:
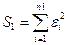 и
и 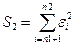 ,
,
где n1 – число наблюдений в первой группе;
n2 – число наблюдений во второй группе.
- если S1> S2 критерий 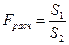 ;
;
- если S2> S1 критерий 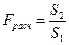 .
.
- чем Fрасч > Fтабл, тем больше нарушена предпосылка о постоянстве дисперсий остаточных величин.
Проверка на независимость ряда остатков
Независимости уровней ряда остатков проверяем по критерию Дарбина-Уотсона.
Вычислить значение:
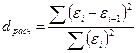 .
.
dрасч сравнивают с нижним d1 и верхним d2, по таблице.
Если dрасч> d1, то гипотеза о независимости ряда остатков выполняется.
Если d1 <dрасч< d1, то используют первым коэффициентом автокорреляции:
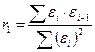 .
.
И если r 1 по модулю меньше табличного критического уровня r крит, то гипотеза о независимости ряда остатков выполняется.
Если d2 < dрасч < 2, то гипотеза о независимости ряда остатков выполняется.
Если dрасч > 2, то модель остатки коррелируют отрицательно,
Необходимо принять за d/ = 4 – d.
Проверка на распределение ряда остатков по нормальному закону
Используем R/S – критерий.
В нашем случае
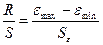 .
.
Расчетное значение R/Sε сравнивают с табличными значениями (нижней и верхней границами данного отношения), и если значение не попадает в интервал между критическими границами, то с заданным уровнем значимости гипотеза о нормальном распределении отвергается; в противном случае гипотеза принимается.
Если ВСЕ вышеперечисленные критерии дают положительный ответ, модель АДЕКВАТНА.
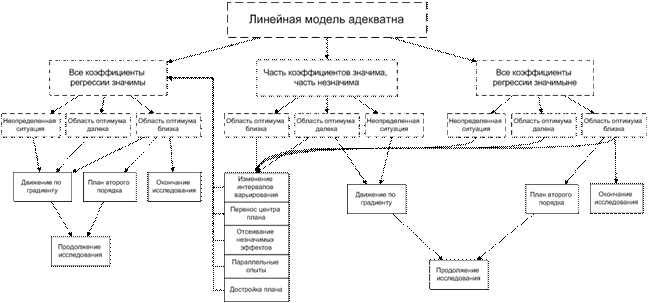
Определение меры точности модели
| Точностные характеристики | Расчет и содержание характеристики |
| Максимальная ошибка | Соответствует Rmax = 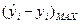
|
| Средняя абсолютная ошибка | 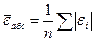 , показывает на сколько в среднем отклоняется фактические значения от модуля. , показывает на сколько в среднем отклоняется фактические значения от модуля.
|
| Дисперсия ряда остатков | 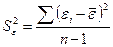 , где , где 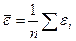
|
| Средняя квадратическая ошибка | 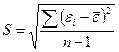 , чем меньше ошибка, тем меньше модуль , чем меньше ошибка, тем меньше модуль
|
| Средняя относительная ошибка аппроксимации | 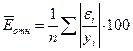 . Допустимый предел значений составляет не более 8 – 15%. . Допустимый предел значений составляет не более 8 – 15%.
|
Точечный и интервальный прогноз
Если модель регрессии адекватна, а параметры модели значимы, то переходят к построению прогноза.
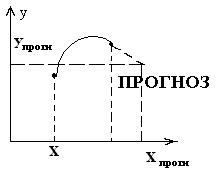
Прогнозное значение результативного признака  определяется путем подстановки в уравнение регрессии
определяется путем подстановки в уравнение регрессии 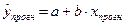 соответствующего (прогнозного) значения
соответствующего (прогнозного) значения 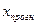 .
.
Далее вычисляется средняя стандартная ошибка прогноза:
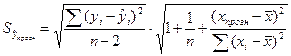 , значит
, значит
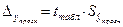 [3]
[3]
и строится доверительный интервал прогноза:
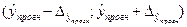 .
.
Пример
Оценить адекватность и точность модели парной регрессии по представленным данным о спросе и доходе населения за ряд текущих лет и сделать выводы.
| Год | Спрос, yi |
| 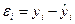
|
| Точки поворота |
|
|
|
| 1 | 6 | 6,1 | -0,10 | 0,01 | - | - | - | 0,017 |
| 2 | 8 | 7,38 | 0,62 | 0,38 | 1 | 0,72 | 0,52 | 0,078 |
| 3 | 8 | 8,66 | -0,66 | 0,44 | 1 | -1,28 | 1,64 | 0,083 |
| 4 | 10,3 | 9,94 | 0,36 | 0,13 | 1 | 1,02 | 1,04 | 0,035 |
| 5 | 10,5 | 11,22 | -0,72 | 0,52 | 1 | -1,08 | 1,17 | 0,069 |
| 6 | 13 | 12,5 | 0,50 | 0,25 | - | 1,22 | 1,49 | 0,038 |
| Итого | 55,8 | - | 0,00 | 1,73 | 4 | - | 5,85 | 0,319 |
Уравнение парной регрессии имеет вид: 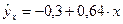 .
.
Проверка адекватности модели осуществляется на основе анализа остатков 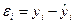 .
.
Проверка значимости модели
Значимость параметров модели оценивается с помощью t – критерия Стьюдента:
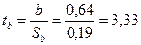 ;
; 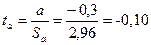 ,
,
где 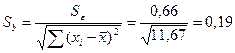 ;
;
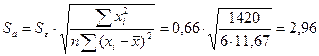 ,
,
где 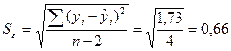 .
.
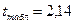 ;
;
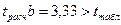 , то параметр b значим;
, то параметр b значим;
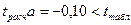 , то параметр a не значим.
, то параметр a не значим.
Для проверки значимости уравнения регрессии в целом используем F критерий Фишера:
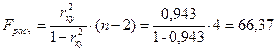 .
.
Воспользуемся встроенными возможности электронных таблиц Excel: FРАСПОБР, которое возвращает обратное значение для F-распределения вероятностей.
Синтаксис функции:
FРАСПОБР(вероятность;степени_свободы1;степени_свободы2)
Вероятность — это вероятность, связанная с F-распределением.
Степени_свободы1 — это числитель степеней свободы.
Степени_свободы2 — это знаменатель степеней свободы.
Fтабл = FРАСПОБР(0,05;1;4) = 7,71
Поскольку: Fрасч > Fтабл, модель считается значимой.
Дата: 2018-11-18, просмотров: 669.