1. Установление численного значения корреляционной связи между изучаемыми признаками путем вычисления (парных, множественных и/или частных) коэффициентов корреляции
2. Измерение тесноты связи между признаками
3. Определение достоверности суждения о наличии связи (с помощью t-критерия Стьюдента)
4. Отбор факторов, оказывающих наибольшее влияние на результативный признак
5. Выявление ранее неизвестных причинных связей
Ковариация
Мерой взаимосвязи между двумя переменными является ковариация. Она построена на сумме отклонений индивидуальных значений признаков xi и yi от их средних значений.
Опр. При наличии n наблюдений двух переменных (x и y) ковариация между x и у задается формулой:
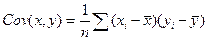 [1].
[1].
При наличии прямой связи ковариация будет положительной.
При наличии обратной связи ковариация будет отрицательной величиной.
При отсутствии связи ковариация будет близка к нулю.
Размер ковариации зависит от масштаба признаков x и y.
Несколько основных правил расчета ковариации
Есть несколько важных правил, которые вытекают непосредственно из определения ковариации:
Правило 1
Если у = v + w, то Cov (x, у) = Cov (x, v) + Cov (x, w).
Правило 2
Если у = az, где a — константа, то Cov (x, у) = a Cov (x, z).
Правило 3
Если у = а, где я — константа, то Cov (x, у) = 0.
Альтернативное выражение для выборочной ковариации
Другим эквивалентным выражением является
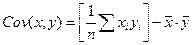
Дисперсия
Опр. Дисперсия это средний квадрат отклонений индивидуальных значений признака от их средней величины:
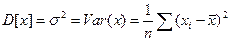 .
.
Она характеризующие степень разброса значений 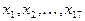 (
( 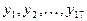 ) вокруг своего среднего
) вокруг своего среднего 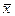 (
( 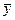 , соответственно), или вариабельность (изменчивость) этих переменных на множестве наблюдений. Отсюда обозначение Var [variance].
, соответственно), или вариабельность (изменчивость) этих переменных на множестве наблюдений. Отсюда обозначение Var [variance].
Впрочем, более естественным было бы измерение степени разброса значений переменных в тех же единицах, в которых измеряется и сама переменная. Эту задачу решает показатель, называемый стандартным отклонением [standard deviance - Std.Dev] переменной 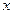 (переменной
(переменной 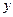 ), определяемый соотношением:
), определяемый соотношением:
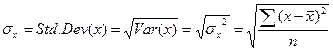 .
.
Правила расчета дисперсии
Существует несколько простых и очень полезных правил для расчета дисперсии, являющихся аналогами правил для ковариации,. Эти правила в равной степени можно использовать как для выборочной, так и для теоретической дисперсии.
Правило дисперсии 1
Если у = v + w, то Var (у) = Var (v) + Var (w) + 2Cov (v,w).
Правило дисперсии 2
Если у = az, где а является постоянной, то Var(y) = a2Var(z).
Правило дисперсии 3
Если у=а, где а является постоянной, то Var (у) = 0.
Правило дисперсии 4
Если у = v + а, где а является постоянной, то Var (у) = Var (v).
Заметим, что дисперсия переменной х может рассматриваться как ковариация между двумя величинами х.
Поэтому 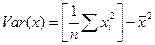 .
.
Дата: 2018-11-18, просмотров: 664.