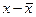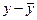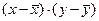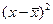1. Установление формы зависимости между переменными,
2. Оценка модельной функции (модельного уравнения) регрессии,
3. Определение неизвестных (прогнозных) значений зависимой переменной.
Иногда в практике экономических исследований, имеющиеся данные нельзя считать выборкой из многомерной нормально распределенной совокупности.
Если результативный признак (Y) подчиняется нормальному закону распределения, а факторные признаки (X) – произвольному закону распределения, для аналитического выражения формы зависимости используют уравнение регрессии.

Замечание
Если для выражения формы корреляционной связи подходит одновременно несколько функций (прямая, полиномы различных порядков, гипербола, степенная и т.п.) желательно дать окончательное обоснование выбора функции для выражения формы связи на альтернативной основе.
Наиболее простой в технике расчетов является линейная форма регрессии.
Линейная парная регрессия
Уравнение парной регрессии имеет вид:
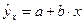
Замечание
Не следует ожидать получения точного соотношения между исследуемыми экономическими показателями. В экономической теории это проблема решается путём аппроксимацией, а в статистическом анализе, данный факт неточности описывается включением в модель случайным остаточным членом:
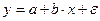
где y - зависимая переменная, состоящая из двух составляющих
a + bx – объясняющая составляющая,
где a - постоянная величина (или свободный член уравнения), показывает значение результативного признака y при равенстве нулю факторного.
b - коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений, показывает на какую величину в среднем изменится y, если переменную x увеличить на единицу измерения.
Если b >0 - переменные Х и Y положительно коррелированные,
Если b< 0 – отрицательно коррелированны.
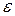 - независимая случайная величина. Она отражает тот факт, что изменение Y будет неточно описываться изменением фактора Х, поскольку в реальной ситуации всегда будут присутствовать другие факторы, неучтенные в данной модели.
- независимая случайная величина. Она отражает тот факт, что изменение Y будет неточно описываться изменением фактора Х, поскольку в реальной ситуации всегда будут присутствовать другие факторы, неучтенные в данной модели.
Для расчета неизвестных параметров a и b пользуется метод наименьших квадратов (МНК). Неизвестные параметры a и b выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений yi от значений 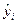 , найденных по уравнению регрессии была минимальной:
, найденных по уравнению регрессии была минимальной:
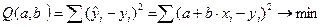 .
.
На основании необходимого условия экстремума функции двух переменных Q(a,b) приравниваем к нулю ее частные производные:
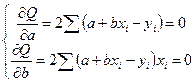
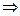
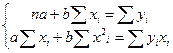 .
.
Последняя система является системой двух линейных уравнений с двумя неизвестными.
Разделив обе части уравнений на n и преобразовав их, получим:
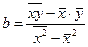 или
или 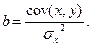
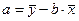 .
.
Коэффициент эластичности
Наряду с коэффициентом регрессии в экономическом анализе часто используется показатель эластичности измерения результативного признака относительно факторного.
Коэффициент эластичности показывает, на сколько процентов изменяется в среднем результативный признак у при изменении факторного признака х на 1%.
Э = 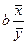
2.4.Формула определения бета - коэффициента
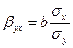
Бета-коэффициент показывает, на какую часть своего среднего квадратического отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину среднего квадратического отклонения.
Пример
По представленным данным о спросе и доходе населения за ряд текущих лет построить уравнение регрессии.
| Год | Доход, Х | Спрос, Y |
|
|
|
|
| 1 | 10 | 6 | -5 | -3,3 | 16,5 | 25 |
| 2 | 12 | 8 | -3 | -1,3 | 3,9 | 9 |
| 3 | 14 | 8 | -1 | -1,3 | 1,3 | 1 |
| 4 | 16 | 10,3 | 1 | 1 | 1 | 1 |
| 5 | 18 | 10,5 | 3 | 1,2 | 3,6 | 9 |
| 6 | 20 | 13 | 5 | 3,7 | 18,5 | 25 |
| Итого | 90 | 55,8 | 0 | 0 | 44,80 | 70,00 |
| Среднее | 15 | 9,3 | 0 | 0 | 7,47 | 11,67 |
Уравнение парной регрессии имеет вид:
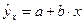
Параметры модели определим по формулам:
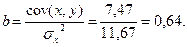
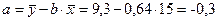
Коэффициент b показывает, что с увеличением дохода на 1 у.е., спрос возрастёт на 0,64 у.е.
Уравнение парной регрессии примет вид:
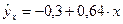 .
.
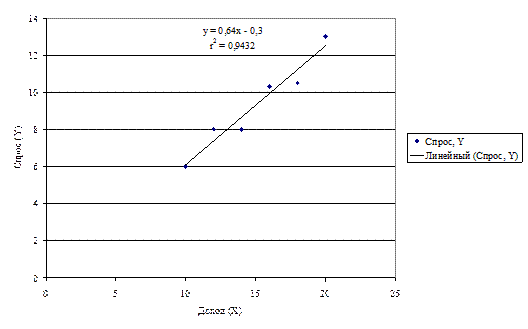
Построим на диаграмме зависимость Y от Х и добавим линию тренда, используя линейную модель для описания данных:
Дата: 2018-11-18, просмотров: 703.