Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Для решения практических задач приходится строить эпюры гидростатического давления, представляющие собой графиче­ское изображение распределения гидростатического давления на плоские прямоугольные поверхности.

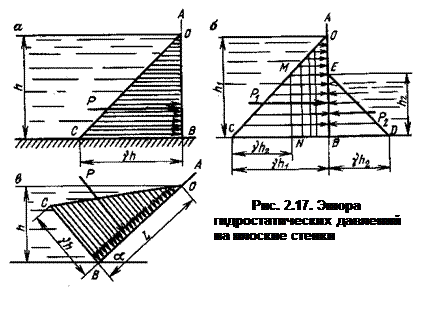Рассмотрим случай определения гидростатического давления на плоскую вертикальную стенку АВ шириной b (рис. 2.17, а), на которую давит жидкость высотой h. Для этого воспользуемся основным уравнением гидростатики 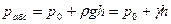, характеризую­щим распределение гидростатического давления по глубине и являющимся уравнением прямой. Следовательно, для построения эпюры гидростатического давления, действующего на стенку, достаточно знать две точки.

Избыточное давление на поверхности равно нулю. У дна резервуара избыточное давление равно .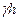

Приняв за начало координат точку О и отложив в выбран­ном масштабе из точки В величину 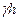 (согласно первому свой­ству гидростатического давления), соединяем полученную точ­ку С и точку О прямой линией. Треугольник ОВС с векторами сил давления называется эпюрой избыточных давлений на плос­кую вертикальную стенку. Полное гидростатическое давление на стенку

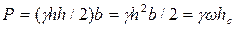
где w — площадь стенки; h_c — центр тяжести площади стенки.

Точку приложения равнодействующей гидростатического давления на плоские поверхности называют центром давления.

Центр давления не совпадает с центром тяжести, а нахо­дится несколько ниже его (на величину, равную отношению мо­мента инерции площади стенки относительно центральной оси к статическому моменту этой площади). Если на вертикальную стенку гидростатическое давление действует с двух сторон, то эпюрой совместного действия будет трапеция OBNM (рис. 2.17, б) и суммарное полное гидростатиче­ское давление на стенку равно их разности:

.

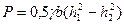Центр давления, найденный на основании уравнения момен­тов равнодействующих сил относительно точки В, будет равен

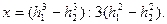
Если плоская стенка АВ (рис. 2.17, в), на которую действует жидкость, наклонена к горизонту под углом a, то основное урав­нение гидростатики применительно к этому случаю может быть записано так:

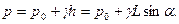
Центр давления пройдет через центр эпюры перпендикулярно наклонной стенке.

 2.11. Давление жидкости на цилиндрические

                          поверхности

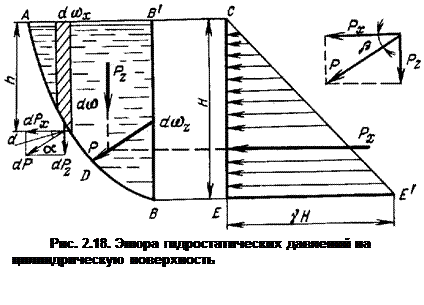Рассмотрим цилиндрическую поверхность АВ (рис. 2.18), под­верженную действию избыточного гидростатического давления. Выделим на этой поверхности бесконечно малую площадку d w , центр тяжести которой погружен в жидкость на глубину h .

На эту элементарную площадку нормально к цилиндрической поверхности будет действовать сила избыточного гидростатиче­ского давления 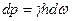, которую можно разложить на гори­зонтальную и вертикальную составляющие, т. е. на силы dp_x и dp_z ,.

Предположим, что сила dp наклонена к горизонту под углом a . Тогда выражения для составляющих сил могут быть записаны так: dp_x = dp cos a и dp_z = dp sin a.

Подставив значение dp в выражение dp_x , получим:

dp_x= g hd w cos a .

Согласно рис. 2.18, d w cos a = d w _z , т. е. проекция элементар­ной полоски d w на вертикальную плоскость. Следовательно, можно записать, что dp_x = g hd w _z . Тогда горизонтальная состав­ляющая полной силы избыточного гидростатического давления на рассматриваемую цилиндрическую поверхность будет опреде­ляться как

.

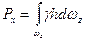Здесь интеграл — статический момент всей площади верти­кальной проекции цилиндрической поверхности  относительно свободной поверхности жидкости. Этот статический момент ра­вен произведению площади вертикальной проекции цилиндриче­ской поверхности 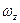на глубину погружения центра ее тяжести h_c , т. е.

.

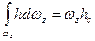Таким образом, горизонтальная составляющая силы избы­точного гидростатического давления, действующего на цилинд­рическую поверхность, равна силе гидростатического давления, под действием которого находится вертикальная стена, по пло­щади равная площади вертикальной проекции рассматриваемой цилиндрической поверхности:

.

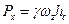Величина этой горизонтальной составляющей может быть также выражена площадью эпюры гидростатического давле­ния СЕЕ'.

Для определения вертикальной составляющей элементарной силы избыточного гидростатического давления можно написать:

.

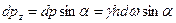Величина 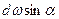 является площадью проекции 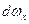, элемен­тарной площадки  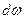на горизонтальную плоскость. Совершенно очевидно, что выражение 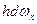представляет собой объем dV призмы, отмеченной на рис. 2.18 штриховкой. Произведение же 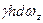является массой жидкости в этом бесконечно малом объ­еме, т. е.

dM = g dV .

Тогда вертикальная составляющая полной силы избыточного гидростатического давления равна

.

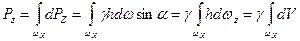Центр давления для цилиндрических поверхностей находится графоаналитическим путем.

Вектор полной силы давления Р должен проходить через точ­ку пересечения ее горизонтальной и вертикальной составляющих

P_X и Р _Z под углом b, определяемым из выражения 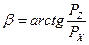. В данном случае центр давления будет расположен в точке пересечения вектора полной силы давления с криволинейной поверхностью АВ (точка D ).